A non-surjective function is one that does not map every element of its codomain to an element in its domain, meaning some values in the codomain remain unmapped. Understanding the concept of non-surjectivity is essential in fields like mathematics and computer science for analyzing function behaviors and their limitations. Explore the rest of the article to deepen your grasp of non-surjective functions and their practical implications.
Table of Comparison
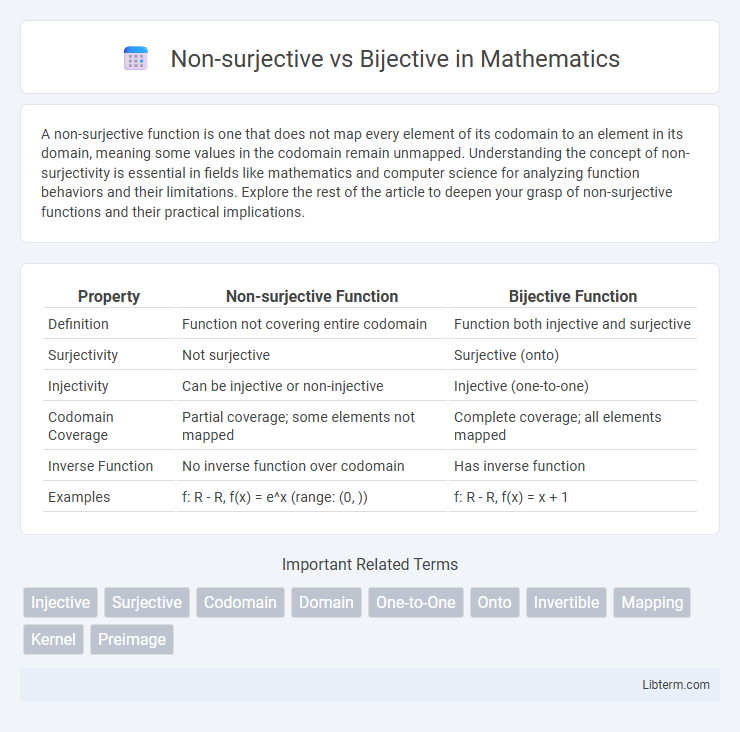
| Property | Non-surjective Function | Bijective Function |
|---|---|---|
| Definition | Function not covering entire codomain | Function both injective and surjective |
| Surjectivity | Not surjective | Surjective (onto) |
| Injectivity | Can be injective or non-injective | Injective (one-to-one) |
| Codomain Coverage | Partial coverage; some elements not mapped | Complete coverage; all elements mapped |
| Inverse Function | No inverse function over codomain | Has inverse function |
| Examples | f: R - R, f(x) = e^x (range: (0, )) | f: R - R, f(x) = x + 1 |
Understanding Functions: Basic Definitions
Non-surjective functions map elements of the domain to a subset of the codomain, leaving some codomain elements unmapped, while bijective functions create a one-to-one correspondence between every element of the domain and codomain. In a bijection, the function is both injective (no two domain elements share the same image) and surjective (every codomain element is mapped), ensuring invertibility. Understanding these basic definitions is essential for grasping function properties in set theory, algebra, and computer science applications.
What Does Non-Surjective Mean?
Non-surjective functions fail to map every element of the function's codomain to at least one element of the domain, meaning some codomain values remain unmatched. In contrast, bijective functions are both injective (one-to-one) and surjective (onto), ensuring every codomain element corresponds to exactly one domain element. Understanding non-surjectivity highlights how functions can be limited in coverage compared to bijections, which offer a perfect pairing between domain and codomain.
Exploring Bijective Functions
Bijective functions establish a perfect one-to-one correspondence between elements of the domain and codomain, ensuring each element is both mapped to and from uniquely. This injective and surjective combination guarantees invertibility, making bijections fundamental in fields like algebra and topology. Understanding bijections enables precise function inversions and underpins concepts such as isomorphisms and permutations.
Surjective vs. Injective: Key Differences
Surjective functions map every element of the codomain to at least one element of the domain, ensuring full coverage of the output set, while injective functions assign unique inputs to distinct outputs, prohibiting overlap in the codomain mapping. The key difference lies in surjectivity requiring all codomain elements to be hit, whereas injectivity demands that no two distinct inputs share the same output. Understanding these distinctions is crucial in fields like linear algebra, set theory, and functional analysis for classifying function types and their invertibility.
Visualizing Non-Surjective Functions
Non-surjective functions leave some elements in the codomain without pre-images, creating gaps in the output range, unlike bijective functions where every element in the codomain is mapped uniquely and completely. Visualizing non-surjective functions often involves mapping arrows from a smaller domain set to a larger codomain where some values remain unpaired, highlighting the incomplete coverage. This distinct image domain representation contrasts sharply with bijections, which ensure a perfect one-to-one correspondence between domain and codomain elements.
Criteria for Bijective Mappings
Bijective mappings require a function to be both injective, meaning each element of the domain maps to a unique element in the codomain, and surjective, where every element of the codomain has a preimage in the domain. Non-surjective functions lack this surjectivity condition, resulting in some codomain elements without corresponding domain elements. Therefore, the key criteria for bijective mappings are one-to-one correspondence and complete coverage of the codomain.
Real-Life Examples: Non-Surjective vs. Bijective
A non-surjective function can be compared to a job application process where not every candidate is hired, indicating some potential applicants are never matched to positions, unlike a bijective function where every applicant is matched to exactly one job, ensuring a perfect one-to-one correspondence. In real life, a non-surjective mapping resembles a school's course enrollment where certain courses receive no students, while bijective mappings reflect a system like a one-to-one locker assignment guaranteeing every student has a unique locker and vice versa. Understanding this distinction helps clarify scenarios where coverage of a range is incomplete versus perfectly paired relationships in practical applications such as database indexing and resource allocation.
Mathematical Implications of Each Type
Non-surjective functions fail to cover the entire codomain, leading to a lack of invertibility since not all outputs have preimages. Bijective functions establish a perfect one-to-one correspondence between domain and codomain, ensuring the existence of a unique inverse function. The mathematical implications of bijectivity include isomorphisms in algebraic structures and invertible transformations in linear algebra, whereas non-surjective mappings limit the scope of such correspondences and inverse operations.
Common Misconceptions Explained
Non-surjective functions are often misunderstood as incomplete or defective mappings, yet they simply do not cover every element in the codomain, unlike bijective functions, which establish a perfect one-to-one correspondence between domain and codomain. A bijective function guarantees both surjectivity (onto) and injectivity (one-to-one), ensuring every element in the codomain has exactly one pre-image, which is a frequent misconception when learners conflate surjectivity with bijectivity. Recognizing that surjectivity alone does not imply injectivity helps clarify that non-surjective functions can still be injective but fail to reach all codomain values, distinguishing them clearly from bijections.
When to Use Non-Surjective or Bijective Functions
Non-surjective functions are ideal when mapping from a larger domain to a smaller codomain where not all elements need to be covered, often in data compression or feature selection scenarios. Bijective functions are essential in cases requiring one-to-one correspondences such as encoding schemes, cryptographic algorithms, and reversible transformations to ensure invertibility. Choosing between non-surjective and bijective mappings depends on whether full codomain coverage and invertibility are necessary for the application.
Non-surjective Infographic
 libterm.com
libterm.com