Filtered colimits are a fundamental concept in category theory, describing the limit of diagrams indexed by filtered categories that capture directed systems. They play a crucial role in algebra, topology, and computer science by enabling the construction of objects from simpler components while preserving essential structure. Explore the rest of the article to deepen your understanding of filtered colimits and their applications.
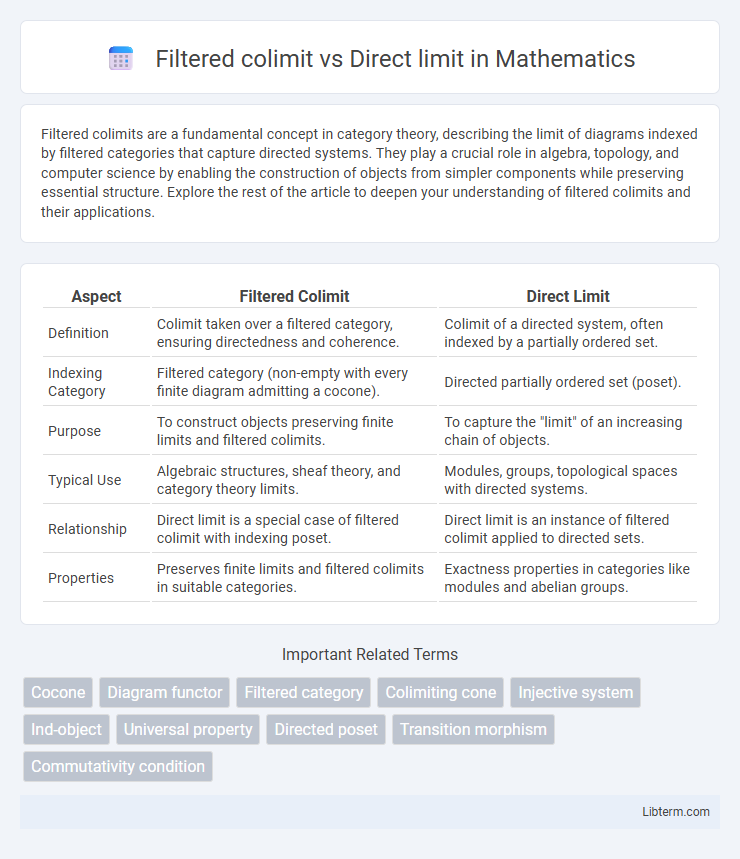
Table of Comparison
| Aspect | Filtered Colimit | Direct Limit |
|---|---|---|
| Definition | Colimit taken over a filtered category, ensuring directedness and coherence. | Colimit of a directed system, often indexed by a partially ordered set. |
| Indexing Category | Filtered category (non-empty with every finite diagram admitting a cocone). | Directed partially ordered set (poset). |
| Purpose | To construct objects preserving finite limits and filtered colimits. | To capture the "limit" of an increasing chain of objects. |
| Typical Use | Algebraic structures, sheaf theory, and category theory limits. | Modules, groups, topological spaces with directed systems. |
| Relationship | Direct limit is a special case of filtered colimit with indexing poset. | Direct limit is an instance of filtered colimit applied to directed sets. |
| Properties | Preserves finite limits and filtered colimits in suitable categories. | Exactness properties in categories like modules and abelian groups. |
Introduction to Filtered Colimit and Direct Limit
Filtered colimits and direct limits are fundamental concepts in category theory used to describe the colimit of diagrams indexed by filtered categories or directed posets, respectively. A filtered colimit generalizes direct limits by allowing the indexing category to be any filtered category, capturing more complex convergence behaviors than directed sets alone. Both constructions unify the process of forming "limits of limits" and play a crucial role in algebra, topology, and algebraic geometry by enabling the passage from local to global structures.
Basic Definitions and Key Concepts
Filtered colimits and direct limits both describe ways to construct objects from directed systems in category theory, where filtered colimits generalize direct limits by requiring the indexing category to be filtered, ensuring the existence of suitable cocones. A direct limit is a special case of a filtered colimit indexed by a directed set, focusing on objects and morphisms that preserve coherence in a linear or partially ordered structure. Key concepts include the universality property, cocones, and the preservation of colimit structures in functors, which are crucial for applications in algebra, topology, and model theory.
Historical Development and Terminology
The distinction between filtered colimits and direct limits emerged in category theory through efforts to generalize inductive limit concepts initially developed in algebra and topology during the mid-20th century. Filtered colimits, introduced to manage collections indexed over filtered categories, extend the notion of direct limits, which were historically defined for diagrams indexed over directed partially ordered sets. Terminology evolved as category theorists formalized these constructs, with "filtered colimit" becoming the preferred term to capture the broader indexing framework beyond the traditional "direct limit" used in module theory and homological algebra.
Category-Theoretic Framework
In category theory, filtered colimits generalize direct limits by indexing over filtered categories, which ensures the existence of cocones that amalgamate directed diagrams consistently. Direct limits are a special case of filtered colimits where the indexing category is a directed poset, often used in algebraic structures like modules and groups. The category-theoretic framework highlights that filtered colimits preserve finite limits in well-behaved categories, providing a robust tool for constructing objects via directed systems beyond partially ordered sets.
Filtered Colimits: Properties and Examples
Filtered colimits preserve finite limits and are crucial in category theory for constructing objects as directed unions of simpler components, ensuring coherence in filtered diagrams. They are especially important in algebra and topology, where filtered colimits of modules, sheaves, or spaces maintain exactness and continuity properties. Examples include filtered colimits of groups indexed by directed posets, illustrating how complex structures emerge from compatible morphisms within filtered categories.
Direct Limits: Properties and Examples
Direct limits, also known as inductive limits, are constructed from directed systems of objects and morphisms in a category, capturing the notion of "limiting" behavior over a directed set. Key properties of direct limits include their exactness in the category of modules and their role in preserving colimits, making them essential in constructing objects like colimits of sequences of groups or rings. Examples of direct limits appear in algebraic topology with the homology of filtered spaces and in algebra through unions of ascending chains of submodules or subgroups.
Differences Between Filtered Colimit and Direct Limit
Filtered colimits and direct limits are categorical concepts often used interchangeably but differ subtly in context and construction. A filtered colimit specifically refers to the colimit over a filtered category, ensuring coherence and the existence of compatible morphisms, which is crucial in algebra and topology for building structures from directed systems. In contrast, a direct limit is a more general term usually synonymous with filtered colimit in many algebraic settings, but may lack the explicit categorical emphasis on the filtering property that guarantees the directedness and existence of certain universal morphisms.
Applications in Algebra and Topology
Filtered colimits provide a flexible framework for constructing objects by gluing directed systems, crucial in algebra for forming inductive limits of modules and rings, enabling the study of properties preserved under such limits. Direct limits, a specific case of filtered colimits often indexed by directed sets, are instrumental in topology for defining spaces as unions of directed systems of subspaces, facilitating analysis of their homotopy and homology. Both concepts underpin key constructions in category theory, allowing algebraists and topologists to handle infinite-dimensional or complex structures through manageable approximations.
Common Misconceptions and Clarifications
Filtered colimits and direct limits often cause confusion due to their similar definitions in category theory; however, filtered colimits require the indexing category to be filtered, meaning every finite diagram has a cocone, ensuring better preservation of finite limits. Direct limits are a special case of filtered colimits indexed by a directed set, emphasizing their role in constructing objects as unions or limits along chains. A common misconception is treating all colimits over directed sets as general colimits without recognizing filteredness conditions, which significantly affect properties like exactness and commutation with other limits.
Summary and Further Reading
Filtered colimits and direct limits are fundamental constructs in category theory with filtered colimits generalizing direct limits by considering diagrams indexed over filtered categories rather than directed sets. Filtered colimits preserve finite limits in many categories, serving as key tools in algebra and topology when constructing objects via directed systems. For further reading, explore Mac Lane's "Categories for the Working Mathematician," Borceux's "Handbook of Categorical Algebra," and the nLab page on filtered colimits for deeper theoretical insights and applications.
Filtered colimit Infographic
 libterm.com
libterm.com