Nilpotent elements in algebra are those that become zero when raised to some power, playing a crucial role in ring theory and linear algebra. Understanding nilpotency can help uncover the structure of algebraic systems and simplify complex calculations. Explore the rest of this article to deepen your knowledge on nilpotent concepts and their applications.
Table of Comparison
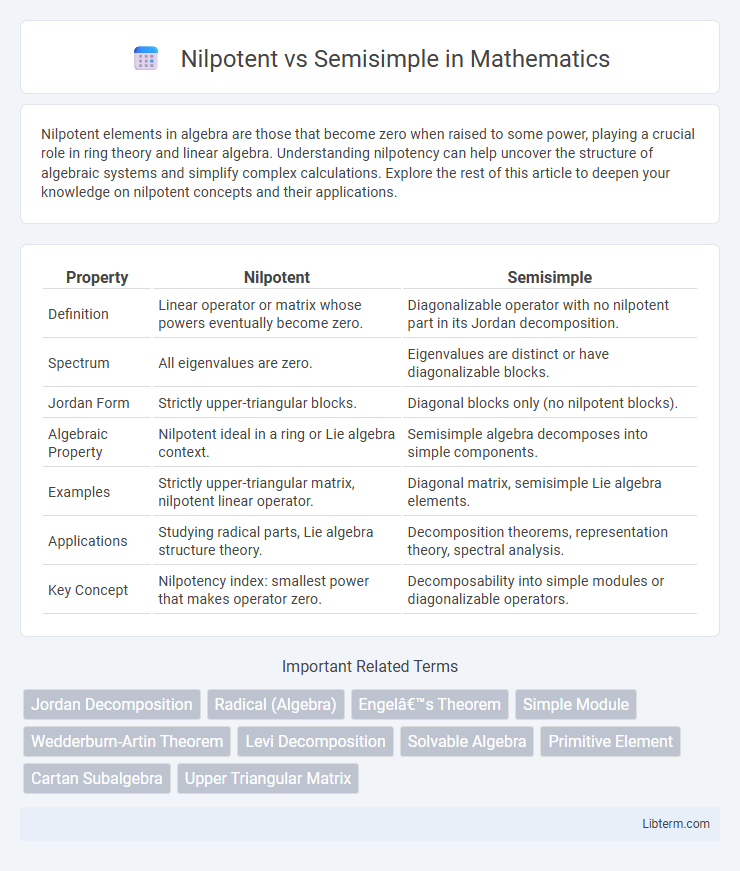
| Property | Nilpotent | Semisimple |
|---|---|---|
| Definition | Linear operator or matrix whose powers eventually become zero. | Diagonalizable operator with no nilpotent part in its Jordan decomposition. |
| Spectrum | All eigenvalues are zero. | Eigenvalues are distinct or have diagonalizable blocks. |
| Jordan Form | Strictly upper-triangular blocks. | Diagonal blocks only (no nilpotent blocks). |
| Algebraic Property | Nilpotent ideal in a ring or Lie algebra context. | Semisimple algebra decomposes into simple components. |
| Examples | Strictly upper-triangular matrix, nilpotent linear operator. | Diagonal matrix, semisimple Lie algebra elements. |
| Applications | Studying radical parts, Lie algebra structure theory. | Decomposition theorems, representation theory, spectral analysis. |
| Key Concept | Nilpotency index: smallest power that makes operator zero. | Decomposability into simple modules or diagonalizable operators. |
Understanding Nilpotent and Semisimple Elements
Nilpotent elements in algebraic structures are characterized by their property that some power of the element equals zero, revealing a deeply constrained and 'vanishing' behavior under iteration. Semisimple elements, contrastingly, decompose into a direct sum of simple modules or eigencomponents, reflecting a structure with no nilpotent part and maximal diagonalizability over an algebraically closed field. Understanding these concepts is crucial in the representation theory of Lie algebras and algebraic groups, where nilpotent elements often identify radical or unipotent parts, and semisimple elements correspond to stable, diagonalizable transformations.
Key Definitions: Nilpotent and Semisimple Explained
Nilpotent operators are linear transformations whose repeated application leads to the zero transformation after a finite number of iterations, characterized by their nilpotency index. Semisimple operators, in contrast, have a diagonalizable structure over an algebraically closed field, decomposing vector spaces into direct sums of simple invariant subspaces. Understanding the distinction between nilpotent and semisimple linear operators is fundamental in linear algebra and representation theory, particularly when analyzing Jordan canonical forms and module decompositions.
Properties of Nilpotent Objects
Nilpotent objects in algebra are characterized by the property that some power of the element (or operator) equals zero, reflecting annihilation under iteration. These entities exhibit a strictly upper-triangularizable structure in linear algebra, where their eigenvalues are all zero and their minimal polynomial is a power of \(x\). Nilpotency ensures that the associated Jordan normal form consists solely of nilpotent Jordan blocks, highlighting their role in decompositions related to the radical of an algebra.
Properties of Semisimple Objects
Semisimple objects in algebraic structures are characterized by their decomposition into direct sums of simple subobjects, which ensures complete reducibility. These objects exhibit rigidity, with every submodule admitting a complement, and semisimplicity implies a zero radical, distinguishing them from nilpotent elements that have strictly vanishing powers. In representation theory, semisimple modules correspond to representations with diagonalizable actions, reflecting their stability under homomorphisms and preserving structural invariants.
Nilpotent vs Semisimple: Core Differences
Nilpotent and semisimple operators differ fundamentally in their algebraic structure: nilpotent operators have all eigenvalues equal to zero and their powers eventually become the zero operator, while semisimple operators can be diagonalized with a basis of eigenvectors corresponding to distinct eigenvalues. The core difference lies in their Jordan normal forms, where a nilpotent matrix consists solely of Jordan blocks with zero eigenvalues, whereas a semisimple matrix is diagonalizable with no nilpotent part. Understanding these distinctions is crucial for applications in linear algebra, particularly in decomposing linear transformations into their semisimple and nilpotent components.
Examples in Algebra and Linear Algebra
Nilpotent elements, such as strictly upper triangular matrices, satisfy the property that some power of the element equals zero, exemplified by the nilpotent matrix N where N2 = 0. Semisimple elements, including diagonalizable matrices with distinct eigenvalues, decompose into direct sums of simple modules without nilpotent parts, like a diagonal matrix D with eigenvalues l1, l2, ..., l_n. In Lie algebra, nilpotent Lie algebras have all adjoint operators nilpotent, for instance, the Heisenberg algebra, while semisimple Lie algebras, such as \( \mathfrak{sl}_2(\mathbb{C}) \), have no nontrivial solvable ideals and decompose into simple components.
Significance in Lie Algebras and Algebraic Groups
Nilpotent and semisimple elements in Lie algebras play crucial roles in the structure theory, with nilpotent elements corresponding to the radical part and semisimple elements relating to the reductive or diagonalizable part. In algebraic groups, semisimple elements are those with diagonalizable conjugacy, essential for classifying representations, while nilpotent elements correspond to unipotent transformations vital in understanding group actions and geometric properties. The Jordan-Chevalley decomposition expresses any element as a sum of commuting nilpotent and semisimple parts, facilitating the analysis of algebraic and representation-theoretic features.
Applications in Representation Theory
Nilpotent and semisimple elements play crucial roles in representation theory by influencing the structure of Lie algebras and their modules. Semisimple elements correspond to diagonalizable actions, enabling the decomposition of representations into direct sums of irreducible modules, which simplifies classification problems. Nilpotent elements generate unipotent subgroups that govern the behavior of indecomposable representations and control the extension of simple modules through Jordan-Chevalley decomposition.
Classification and Decomposition Theorems
Nilpotent and semisimple Lie algebras are distinguished through classification and decomposition theorems, with Cartan's and Levi's theorems playing central roles. Nilpotent Lie algebras exhibit a lower central series terminating in zero, while semisimple Lie algebras decompose into direct sums of simple Lie algebras with no nontrivial solvable ideals. The Levi decomposition states any finite-dimensional Lie algebra over a field of characteristic zero can be expressed as a semidirect product of its solvable radical and a semisimple subalgebra, highlighting the structural contrast between nilpotent and semisimple components.
Practical Implications in Mathematics
Nilpotent and semisimple elements play crucial roles in linear algebra and representation theory, with nilpotent operators corresponding to strictly upper-triangular matrices and semisimple operators corresponding to diagonalizable matrices. Understanding the Jordan-Chevalley decomposition enables the separation of a linear transformation into its nilpotent and semisimple parts, facilitating the analysis of invariant subspaces and simplifying the solution of differential equations. Practical implications include applications in Lie algebra classification, the study of dynamical systems, and simplifying the structure of algebraic groups.
Nilpotent Infographic
 libterm.com
libterm.com