A CW complex is a type of topological space constructed by gluing cells of different dimensions together in a specific way, making it a fundamental tool in algebraic topology. It allows for a structured way to study complex shapes by breaking them down into simpler building blocks called cells, which include points, lines, disks, and higher-dimensional analogs. Discover how CW complexes provide insight into the shape and structure of spaces and their applications by reading the rest of the article.
Table of Comparison
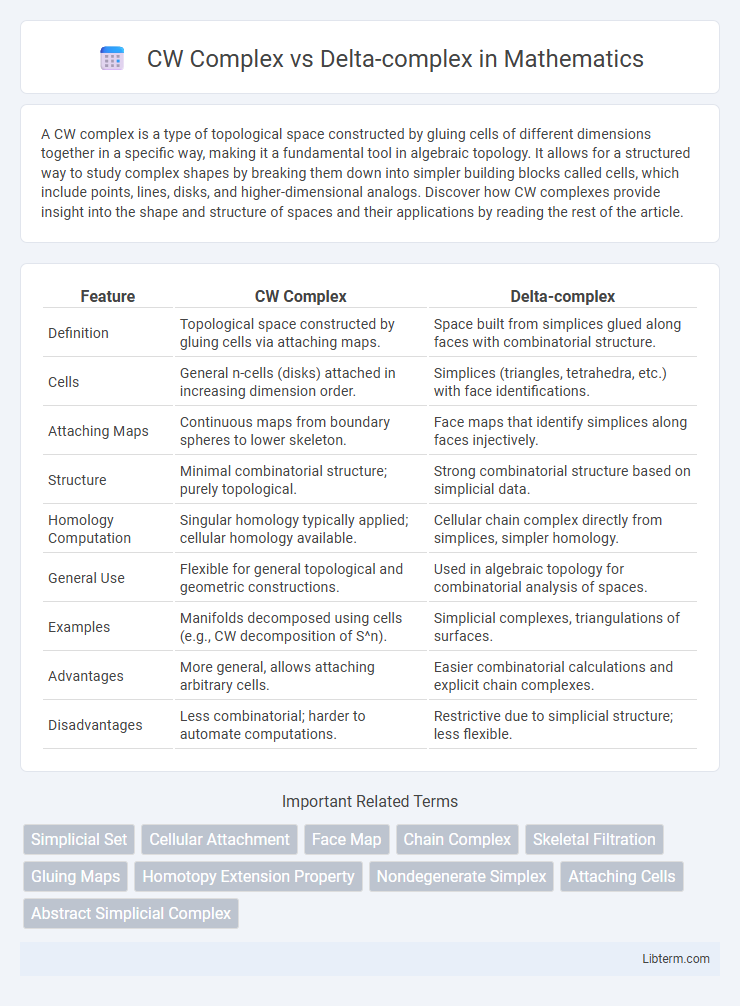
| Feature | CW Complex | Delta-complex |
|---|---|---|
| Definition | Topological space constructed by gluing cells via attaching maps. | Space built from simplices glued along faces with combinatorial structure. |
| Cells | General n-cells (disks) attached in increasing dimension order. | Simplices (triangles, tetrahedra, etc.) with face identifications. |
| Attaching Maps | Continuous maps from boundary spheres to lower skeleton. | Face maps that identify simplices along faces injectively. |
| Structure | Minimal combinatorial structure; purely topological. | Strong combinatorial structure based on simplicial data. |
| Homology Computation | Singular homology typically applied; cellular homology available. | Cellular chain complex directly from simplices, simpler homology. |
| General Use | Flexible for general topological and geometric constructions. | Used in algebraic topology for combinatorial analysis of spaces. |
| Examples | Manifolds decomposed using cells (e.g., CW decomposition of S^n). | Simplicial complexes, triangulations of surfaces. |
| Advantages | More general, allows attaching arbitrary cells. | Easier combinatorial calculations and explicit chain complexes. |
| Disadvantages | Less combinatorial; harder to automate computations. | Restrictive due to simplicial structure; less flexible. |
Introduction to CW Complexes and Delta-Complexes
CW complexes are topological spaces constructed by gluing cells of varying dimensions together, providing a flexible framework for studying homotopy and homology theories. Delta-complexes, alternatively, use simplices glued along faces with combinatorial data specifying identifications, making them suitable for computational topology and simplicial homology. Both structures enable decomposition of spaces into manageable pieces, but CW complexes emphasize cell attachments and weak topology, while Delta-complexes rely on simplicial structures and face maps.
Historical Background and Development
CW complexes, introduced by J.H.C. Whitehead in the 1940s, provided a flexible framework for understanding topological spaces through cell attachments categorized by closure-finite and weak topology conditions. Delta-complexes, emerging from the simplicial approaches in algebraic topology, extend simplicial complexes by allowing more general gluings of simplices while retaining combinatorial tractability crucial for homology computations. The development of these concepts reflects a shift from rigid simplicial structures to more adaptable cellular models, facilitating advancements in homotopy theory and algebraic topology.
Definition of CW Complex
A CW complex is a topological space constructed by iteratively attaching cells of varying dimensions using continuous maps from the boundary of an n-dimensional disk to the existing complex, ensuring closure-finiteness and the weak topology condition. This definition emphasizes the inductive building process starting with 0-cells (points), adding 1-cells (lines), and so forth, while maintaining cellular structure compatibility. Unlike Delta-complexes, which use simplices glued via face maps, CW complexes provide greater flexibility by allowing arbitrary attaching maps, enabling a broader class of spaces to be modeled effectively.
Definition of Delta-Complex
A Delta-complex is a combinatorial structure defined by gluing standard simplices along their faces using affine face maps, allowing a more flexible construction compared to CW complexes, which are built from cells attached via characteristic maps. Delta-complexes facilitate explicit simplicial computations and provide a framework for defining simplicial chain complexes, making them suitable for algebraic topology methods. Unlike CW complexes that may attach cells in a more general manner, Delta-complexes require the gluings to respect simplicial face structure, enabling precise control over the simplicial decomposition of a space.
Construction Process: Step-by-Step Comparison
CW complexes build spaces by inductively attaching cells in increasing dimension using characteristic maps, ensuring closure-finiteness and weak topology conditions. Delta-complexes assemble simplices by identifying their faces through affine maps, emphasizing a combinatorial structure with explicit simplicial decompositions. The CW complex construction focuses on general attaching maps and topological flexibility, while Delta-complexes rely on strict simplicial gluing rules for a more discrete, combinatorial framework.
Attaching Maps: CW Complex vs Delta-Complex
Attaching maps in CW complexes are continuous functions from spheres \( S^{n-1} \) to the \( (n-1) \)-skeleton, allowing cells to be glued in a broad, flexible manner without strict combinatorial restrictions. In contrast, Delta-complexes use simplicial attaching maps that identify faces of simplices linearly and combinatorially, ensuring each n-simplex is glued via affine maps preserving the simplicial structure. This key difference in attaching maps leads to CW complexes having more general topological flexibility while Delta-complexes maintain a rigid combinatorial framework ideal for simplicial homology computations.
Cell Structure and Simplicial Structure
CW complexes utilize cells constructed by attaching n-dimensional disks via continuous maps to form a topological space, emphasizing flexible cell structure with generalized attaching maps. Delta-complexes depend on simplices glued along faces through affine maps, preserving a strict simplicial structure that facilitates combinatorial analysis. The cell structure in CW complexes allows for greater topological versatility, whereas the simplicial structure in Delta-complexes enables explicit computations in homology and simplicial sets.
Examples of CW Complexes and Delta-Complexes
CW complexes include familiar examples such as spheres, tori, and projective spaces constructed by gluing cells of varying dimensions via continuous attaching maps. Delta-complexes generalize simplicial complexes and allow for examples like a triangulated torus or Klein bottle created by identifying simplices along faces with specified orientations. Both frameworks handle cell attachments, but CW complexes emphasize cells with characteristic maps and cellular structure, while delta-complexes rely on ordered simplices and face identifications for combinatorial decompositions.
Applications in Algebraic Topology
CW complexes provide a flexible and general framework for constructing topological spaces by inductively attaching cells, facilitating homology and cohomology computations in algebraic topology. Delta-complexes, defined by gluing simplices along faces, offer a combinatorial model particularly suited for explicitly calculating simplicial homology and for algorithmic applications. Both structures enable the study of homotopy and homology groups, but CW complexes often accommodate more complex spaces, while Delta-complexes streamline computations in simplicial contexts.
Advantages and Limitations of Each Structure
CW complexes offer a flexible and general framework for constructing topological spaces with well-defined cell attachments, enabling efficient computation of homology and homotopy groups, but their abstract construction can complicate explicit combinatorial descriptions. Delta-complexes provide a combinatorial and simplicial approach with clear geometric intuition and straightforward subdivision, facilitating explicit calculations and algorithmic implementations, yet they may restrict the types of cells used and impose more rigid gluing conditions compared to CW complexes. While CW complexes excel in handling diverse topological spaces with fewer combinatorial restrictions, Delta-complexes are advantageous for computational topology and explicit simplicial approximations.
CW Complex Infographic
 libterm.com
libterm.com