Singular refers to the form of a word used to denote one person, place, thing, or concept, distinguishing it from plural forms. Understanding singular forms is essential for proper grammar and clear communication in English. Explore the rest of the article to master singular usage and improve your language skills.
Table of Comparison
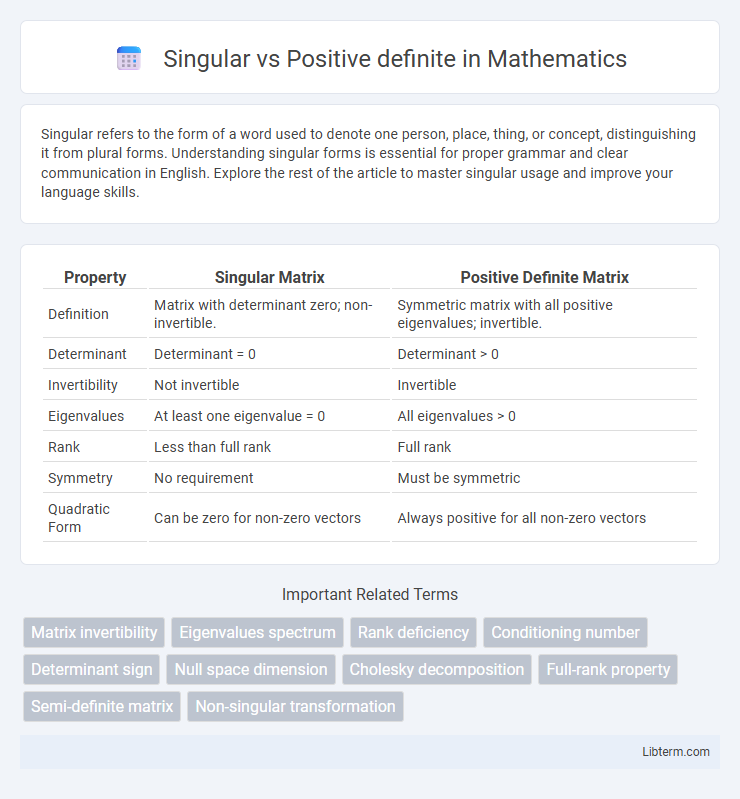
| Property | Singular Matrix | Positive Definite Matrix |
|---|---|---|
| Definition | Matrix with determinant zero; non-invertible. | Symmetric matrix with all positive eigenvalues; invertible. |
| Determinant | Determinant = 0 | Determinant > 0 |
| Invertibility | Not invertible | Invertible |
| Eigenvalues | At least one eigenvalue = 0 | All eigenvalues > 0 |
| Rank | Less than full rank | Full rank |
| Symmetry | No requirement | Must be symmetric |
| Quadratic Form | Can be zero for non-zero vectors | Always positive for all non-zero vectors |
Understanding Singular and Positive Definite Matrices
Singular matrices have a determinant of zero and lack an inverse, indicating linear dependence among their rows or columns. Positive definite matrices are symmetric with all positive eigenvalues, ensuring that for any nonzero vector x, the quadratic form xTAx is positive. These properties are crucial in numerical analysis, optimization problems, and machine learning algorithms for stability and convergence guarantees.
Core Differences: Singular vs Positive Definite
Singular matrices have a determinant equal to zero and do not possess an inverse, indicating linear dependence among their rows or columns. Positive definite matrices are symmetric with all positive eigenvalues, ensuring they are invertible and represent quadratic forms that produce strictly positive values except at the zero vector. The core difference lies in invertibility and eigenvalue characteristics: singular matrices lack full rank and invertibility, while positive definite matrices have full rank with strictly positive eigenvalues.
Mathematical Definitions and Properties
A singular matrix is defined as a square matrix with a determinant of zero, indicating it does not have an inverse and its columns or rows are linearly dependent. A positive definite matrix is a symmetric matrix where all eigenvalues are positive, ensuring it produces strictly positive quadratic forms for any non-zero vector. The key property distinguishing them is that positive definite matrices are always invertible and non-singular, enabling stable solutions in optimization and numerical analysis.
Criteria for Matrix Singularity
Matrix singularity is determined by whether its determinant equals zero, indicating it is singular and not invertible. A positive definite matrix always has a positive determinant and all positive eigenvalues, ensuring it is nonsingular. The critical criterion for singularity is the presence of zero eigenvalues, which directly causes the determinant to be zero, distinguishing singular matrices from positive definite ones.
Identifying Positive Definite Matrices
Positive definite matrices are characterized by all their eigenvalues being strictly positive, ensuring that for any non-zero vector x, the quadratic form xTAx is always positive. Singular matrices, in contrast, have at least one zero eigenvalue, causing them to lack invertibility and making the quadratic form non-strictly positive or zero for some vector x. Identifying positive definite matrices involves checking eigenvalue positivity, verifying positive pivots in Cholesky decomposition, or confirming that all leading principal minors are positive, which guarantees stability in optimization and numerical algorithms.
Applications in Linear Algebra
Singular matrices have zero determinant and lack an inverse, limiting their use in solving linear systems and matrix decompositions. Positive definite matrices, characterized by all positive eigenvalues, are crucial in optimization problems and stable numerical methods like Cholesky decomposition. Applications in machine learning and statistics rely heavily on positive definite covariance matrices to ensure meaningful variance structures and convergence in algorithms.
Implications for System Solvability
Singular matrices, characterized by a zero determinant, indicate dependent equations and lead to an infinite number of solutions or no solution, thus challenging system solvability. Positive definite matrices possess strictly positive eigenvalues, ensuring unique and stable solutions in linear systems through invertibility and well-posedness. In numerical analysis, positive definiteness facilitates the use of efficient algorithms like Cholesky decomposition, while singularity requires alternative approaches such as regularization or pseudoinverse methods.
Eigenvalues and Matrix Characterization
Singular matrices have at least one zero eigenvalue, indicating a determinant of zero and a lack of full rank, which makes them non-invertible. Positive definite matrices possess strictly positive eigenvalues, ensuring all principal minors are positive and the matrix is symmetric with full rank. The characterization of matrices through eigenvalues helps distinguish singular matrices by their zero eigenvalues and positive definite matrices by their strictly positive spectrum.
Practical Examples and Use Cases
Singular matrices, characterized by a determinant of zero, frequently arise in linear systems exhibiting dependency among variables, such as in solving linear equations with infinite or no solutions in economic modeling. Positive definite matrices, defined by all positive eigenvalues, are essential in optimization problems, ensuring convexity and stability, commonly used in machine learning algorithms like support vector machines and portfolio optimization in finance. Practical use cases for singular matrices include data compression and dimensionality reduction, while positive definite matrices are crucial in covariance matrix estimation and quadratic form evaluations in engineering design.
Testing and Verifying Matrix Type
Testing a matrix for singularity involves computing its determinant or checking its rank to determine if it is invertible, as a singular matrix has a determinant of zero and lacks full rank. Verifying positive definiteness requires checking whether all eigenvalues are positive or employing criteria such as the leading principal minors being positive, ensuring the matrix meets properties necessary for optimization and stability in numerical methods. Efficient algorithms like Cholesky decomposition confirm positive definiteness, whereas failure in matrix factorization can indicate singularity or non-positive definiteness.
Singular Infographic
 libterm.com
libterm.com