A measurable set is a fundamental concept in measure theory, describing a set for which a consistent measure, such as length, area, or probability, can be assigned. These sets allow for precise quantification and analysis within mathematical frameworks, ensuring that operations like union and intersection preserve measurability. Explore the rest of the article to understand how measurable sets underpin modern mathematics and their applications in real-world problems.
Table of Comparison
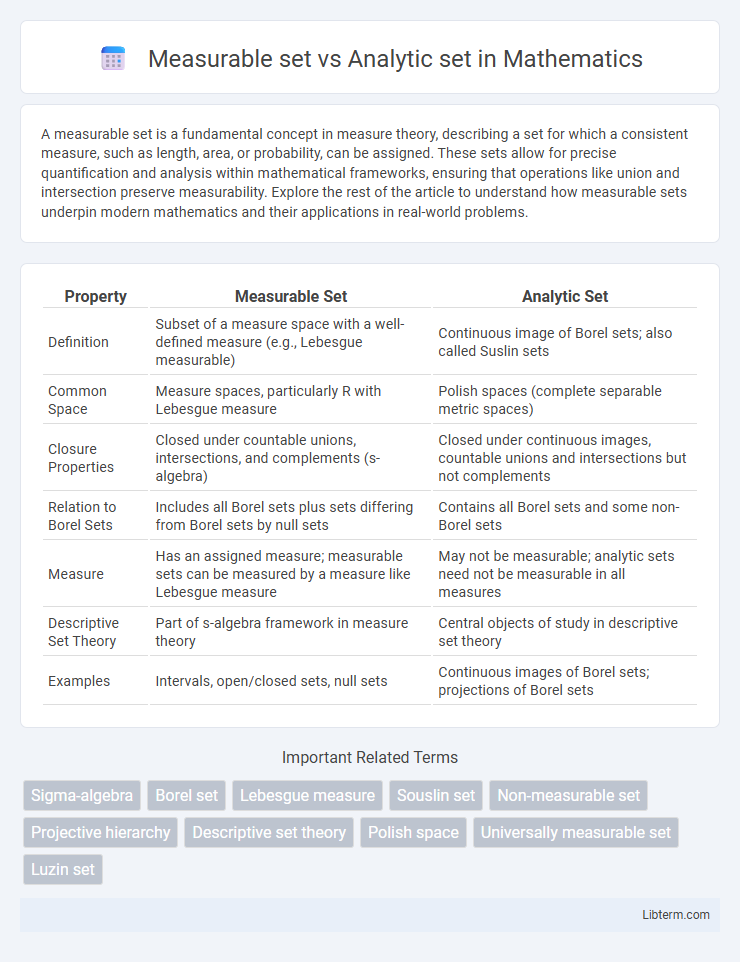
| Property | Measurable Set | Analytic Set |
|---|---|---|
| Definition | Subset of a measure space with a well-defined measure (e.g., Lebesgue measurable) | Continuous image of Borel sets; also called Suslin sets |
| Common Space | Measure spaces, particularly R with Lebesgue measure | Polish spaces (complete separable metric spaces) |
| Closure Properties | Closed under countable unions, intersections, and complements (s-algebra) | Closed under continuous images, countable unions and intersections but not complements |
| Relation to Borel Sets | Includes all Borel sets plus sets differing from Borel sets by null sets | Contains all Borel sets and some non-Borel sets |
| Measure | Has an assigned measure; measurable sets can be measured by a measure like Lebesgue measure | May not be measurable; analytic sets need not be measurable in all measures |
| Descriptive Set Theory | Part of s-algebra framework in measure theory | Central objects of study in descriptive set theory |
| Examples | Intervals, open/closed sets, null sets | Continuous images of Borel sets; projections of Borel sets |
Introduction to Measurable and Analytic Sets
Measurable sets are fundamental objects in measure theory characterized by their compatibility with a given measure, such as the Lebesgue measure, allowing the assignment of a consistent size or volume. Analytic sets, arising in descriptive set theory, are projections of Borel sets from a higher-dimensional space and often exhibit more complex structures than Borel or measurable sets. Understanding the distinction and relationship between measurable and analytic sets is essential for advanced analysis, as analytic sets can be non-measurable yet retain significant topological and descriptive properties used in classification and decomposition problems.
Definitions: Measurable Sets Explained
Measurable sets, defined within measure theory, are subsets of a space for which a measure, such as the Lebesgue measure, can be consistently assigned, ensuring the set's size or volume is well-defined. In contrast, analytic sets are projections of Borel sets and may not always be measurable, representing a broader class within descriptive set theory. Understanding measurable sets involves grasping sigma-algebras and Caratheodory's criterion, which guarantee measurability and integration applicability.
What is an Analytic Set?
An analytic set is a subset of a Polish space that can be expressed as the continuous image of a Borel set from another Polish space, making it a broadly definable class beyond Borel sets. Unlike measurable sets, which are defined by their adherence to a sigma-algebra and allow for measure assignment, analytic sets may not be measurable but are universally measurable under certain conditions. These sets play a crucial role in descriptive set theory, providing a framework for studying complex sets that arise from projections and continuous mappings.
Key Differences Between Measurable and Analytic Sets
Measurable sets are defined within a sigma-algebra associated with a measure, ensuring well-defined measures like Lebesgue measure, while analytic sets arise as continuous images of Borel sets in Polish spaces and are universally measurable but not always Borel. Key differences include that measurable sets form a sigma-algebra closed under countable unions and complements, whereas analytic sets, although closed under continuous images and countable operations, may not be measurable in all measure spaces. Analytic sets are significant in descriptive set theory due to their complexity, contrasting with measurable sets primarily studied in measure theory for integration and probability.
Properties of Measurable Sets
Measurable sets are subsets of a measure space that can be assigned a consistent measure, typically satisfying properties like closure under countable unions, countable intersections, and complementation, thus forming a s-algebra. These sets possess exact measure values enabling integral definitions and support operations crucial for probability theory and real analysis, such as measurability of functions defined on them. In contrast, analytic sets, while generally more complex and measurable in a broader sense, may not share these strong closure properties or be directly associated with a measure in the traditional Lebesgue sense.
Properties of Analytic Sets
Analytic sets, defined as continuous images of Borel sets in Polish spaces, are universally measurable and have the property of being the projection of Borel sets, making them Suslin sets. Every analytic set is Souslin measurable, and they are closed under continuous images and countable unions but not necessarily under complements. These sets play a crucial role in descriptive set theory due to their stability under operations like countable unions and intersections, and their measure-theoretic regularity properties such as possessing the property of Baire and Lebesgue measurability.
Relationships Between Analytic and Measurable Sets
Measurable sets, defined within a sigma-algebra and equipped with a measure like the Lebesgue measure, form a foundational class in measure theory, while analytic sets, derived as continuous images of Borel sets, extend beyond Borel measurability and exhibit complex descriptive properties. Every analytic set in a Polish space is universally measurable, meaning it is measurable with respect to every complete probability measure that makes all Borel sets measurable. The relationship highlights that analytic sets, although possibly non-Borel, maintain measurability under completed measures, ensuring their significance in advanced probability theory and descriptive set theory.
Examples of Measurable vs Analytic Sets
A measurable set in a standard measure space, such as a Lebesgue measurable subset of the real line, includes intervals like [0,1] or countable unions of such intervals, which are explicitly definable and measurable by Lebesgue measure. An analytic set, for example, the projection of a Borel subset of the plane onto the real line, may fail to be Borel measurable yet remains universally measurable and exhibits more complex descriptive set-theoretic properties. Classic examples highlight that all Borel sets are both measurable and analytic, while some analytic sets constructed via projection are not Borel measurable but still retain measurability in the broader sense.
Applications in Measure Theory and Descriptive Set Theory
Measurable sets, defined through sigma-algebras and measure functions, play a crucial role in measure theory by enabling rigorous integration, probability calculations, and function analysis. Analytic sets, originating in descriptive set theory as projections of Borel sets, extend the class of measurable sets and are vital for studying definability and complexity within Polish spaces. Their applications intertwine, with analytic sets ensuring measurability under certain conditions and supporting advanced results in real analysis, probability, and the classification of sets beyond the Borel hierarchy.
Summary and Key Insights
Measurable sets are subsets of a measure space that can be well-defined and assigned a measure, typically within the framework of sigma-algebras such as Borel or Lebesgue measurable sets in real analysis. Analytic sets, also known as Suslin sets, extend beyond Borel sets and are obtained as continuous images of Borel sets, frequently retaining key properties useful in descriptive set theory and measure theory. While all Borel sets are both measurable and analytic, certain analytic sets are non-Borel yet remain universally measurable, highlighting the subtle distinctions and hierarchical complexity between measurability and analytic classification.
Measurable set Infographic
 libterm.com
libterm.com