Bundles offer a cost-effective way to purchase multiple products or services together, providing both convenience and savings. By choosing a bundle, you can simplify your shopping experience and often access exclusive deals unavailable with individual items. Explore the rest of the article to discover how bundles can maximize your value and meet your specific needs.
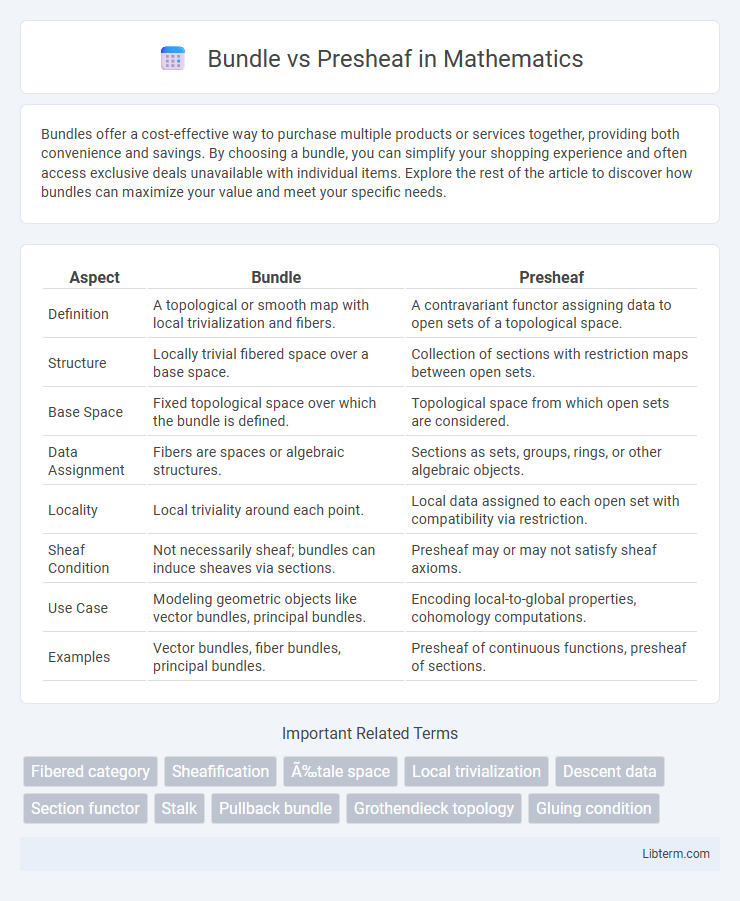
Table of Comparison
| Aspect | Bundle | Presheaf |
|---|---|---|
| Definition | A topological or smooth map with local trivialization and fibers. | A contravariant functor assigning data to open sets of a topological space. |
| Structure | Locally trivial fibered space over a base space. | Collection of sections with restriction maps between open sets. |
| Base Space | Fixed topological space over which the bundle is defined. | Topological space from which open sets are considered. |
| Data Assignment | Fibers are spaces or algebraic structures. | Sections as sets, groups, rings, or other algebraic objects. |
| Locality | Local triviality around each point. | Local data assigned to each open set with compatibility via restriction. |
| Sheaf Condition | Not necessarily sheaf; bundles can induce sheaves via sections. | Presheaf may or may not satisfy sheaf axioms. |
| Use Case | Modeling geometric objects like vector bundles, principal bundles. | Encoding local-to-global properties, cohomology computations. |
| Examples | Vector bundles, fiber bundles, principal bundles. | Presheaf of continuous functions, presheaf of sections. |
Introduction to Bundles and Presheaves
Bundles generalize the concept of a product space by associating a fiber space systematically to every point in a base space, forming a continuous projection map often studied in topology and differential geometry. Presheaves, on the other hand, assign algebraic or categorical structures to open subsets of a topological space, encoding local data with restriction maps obeying compatibility conditions. Both frameworks enable rigorous analysis of local-to-global properties, but bundles emphasize geometric fiber structures, whereas presheaves focus on organizing local information algebraically.
Fundamental Concepts in Topology
Bundles in topology consist of a total space, a base space, and a continuous surjection satisfying local triviality, often exemplified by fiber bundles where each fiber resembles a standard space. Presheaves assign algebraic structures or sets to open subsets of a topological space, capturing local data and restriction maps without necessarily fulfilling gluing axioms present in sheaves. The fundamental distinction lies in bundles providing geometric structures over spaces, while presheaves encode local algebraic information systematically across topological open sets.
Definition of Bundles
A bundle consists of a total space E, a base space B, and a continuous surjective projection map p: E - B, where each fiber p-1(b) is homeomorphic to a typical fiber F, often a topological space or manifold. Bundles provide a geometric structure that locally resembles a product space B x F but may have a global twist, distinguishing them from trivial products. This local triviality condition is central to the formal definition of fiber bundles, including vector bundles and principal bundles.
Definition of Presheaves
A presheaf on a topological space X assigns to each open set U a set (or algebraic structure) F(U) and to each inclusion of open sets V U a restriction map F(U) - F(V) satisfying identity and composition conditions. Unlike bundles, which require local triviality and continuous projection maps, presheaves abstractly encode local data and their restrictions without enforcing gluing or locality conditions. This generalizes sheaves by relaxing the requirement that compatible local sections must uniquely glue together.
Key Differences Between Bundles and Presheaves
Bundles consist of a total space and a base space linked by a continuous surjective map, locally resembling a product space, facilitating the study of geometric objects like vector fields. Presheaves assign data to open sets of a topological space and provide restriction maps between these data, serving as a foundational tool in sheaf theory and category theory. While bundles emphasize local triviality and geometric structure, presheaves focus on systematically organizing local data and morphisms without requiring local triviality or a total space.
Structural Properties and Examples
Bundles are geometric objects consisting of a total space, base space, and projection map, characterized by local triviality and fiber structure; they facilitate the study of continuous variations of fibers over a base. Presheaves assign algebraic data to open subsets of a topological space, capturing local-to-global principles through contravariant functors; typical examples include the sheaf of continuous functions or sections of a bundle. Structural differences highlight that bundles encode fiberwise geometric structures, whereas presheaves abstractly organize local data without inherent geometric fibers, often serving as stepping stones toward sheaves and cohomological methods.
Morphisms: Bundle Maps vs Presheaf Morphisms
Bundle maps are morphisms between fiber bundles that preserve the projection structure, typically defined as continuous maps f: E - E' satisfying p' f = p, where p and p' are the projections of the bundles. Presheaf morphisms are natural transformations between presheaves, consisting of a family of morphisms that commute with restriction maps across open sets in the base space. While bundle maps emphasize maintaining fiber structure and projection compatibility, presheaf morphisms focus on the coherent transformation of sections over varying open subsets, reflecting functorial behavior in the category of presheaves.
Applications in Mathematics and Physics
Bundles, such as fiber bundles, provide a geometric framework crucial for modeling continuous fields and gauge theories in physics, while presheaves offer a categorical approach to local-to-global data organization in topology and algebraic geometry. In mathematics, bundles facilitate the study of smooth manifolds and characteristic classes, whereas presheaves underpin sheaf theory, enabling abstract cohomology theories and descent conditions. Their interplay enhances the formalism of modern mathematical physics, especially in gauge field theory and complex geometry.
Relationship with Sheaves and Fiber Bundles
A bundle generalizes the concept of a fiber bundle by associating a space with fibers parameterized over a base space, while a presheaf assigns data to open sets in a topological space satisfying contravariant functoriality. Sheaves refine presheaves by imposing locality and gluing conditions, making them central in the study of local-to-global properties, and fiber bundles correspond to locally trivial bundles where each fiber is homeomorphic to a fixed space. The relationship connects fiber bundles as geometric constructs modeled by locally trivial bundles, with sheaves providing algebraic and categorical frameworks to study sections and local data, bridging topology and algebraic geometry.
Summary and Future Perspectives
Bundles, specifically fiber bundles, provide a geometric framework for associating a space (the fiber) with every point of a base space, enabling topological and differential structures to be studied globally. Presheaves generalize this notion by assigning algebraic or categorical data to open sets of a topological space, capturing local-to-global relationships abstractly through restriction morphisms. Future research aims to deepen the integration of homotopical and higher-categorical methods with presheaf theory, enhancing applications in derived geometry, topological quantum field theory, and complex systems modeling.
Bundle Infographic
 libterm.com
libterm.com