The Fs set is a fundamental concept in topology and real analysis, defined as a countable union of closed sets. These sets play a crucial role in understanding the structure of measurable and Borel sets, impacting areas such as descriptive set theory. Explore the rest of the article to deepen your understanding of Fs sets and their applications.
Table of Comparison
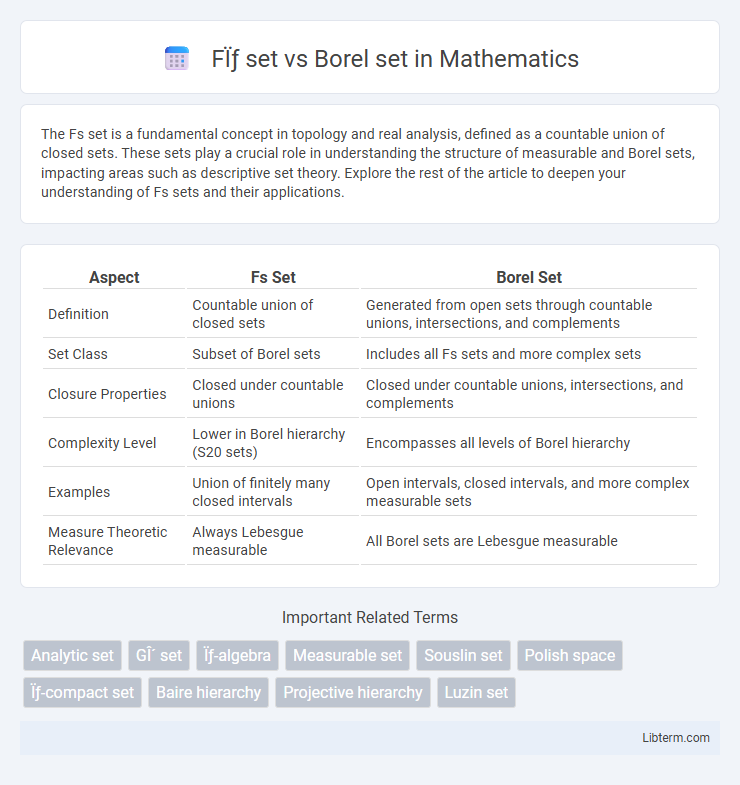
| Aspect | Fs Set | Borel Set |
|---|---|---|
| Definition | Countable union of closed sets | Generated from open sets through countable unions, intersections, and complements |
| Set Class | Subset of Borel sets | Includes all Fs sets and more complex sets |
| Closure Properties | Closed under countable unions | Closed under countable unions, intersections, and complements |
| Complexity Level | Lower in Borel hierarchy (S20 sets) | Encompasses all levels of Borel hierarchy |
| Examples | Union of finitely many closed intervals | Open intervals, closed intervals, and more complex measurable sets |
| Measure Theoretic Relevance | Always Lebesgue measurable | All Borel sets are Lebesgue measurable |
Introduction to Fσ Sets and Borel Sets
Fs sets are countable unions of closed sets, forming an important class within descriptive set theory and general topology. Borel sets, generated from open sets through countable unions, countable intersections, and complements, encompass all Fs sets as they form the smallest s-algebra containing open sets. Understanding the hierarchy of Fs sets within the broader Borel s-algebra is fundamental for measure theory, real analysis, and probability theory.
Definitions: Fσ Sets Explained
An Fs set is defined as a countable union of closed sets within a topological space, making it a significant concept in descriptive set theory and real analysis. These sets are always Borel sets because the Borel s-algebra is generated by open sets, and closed sets can be expressed as complements of open sets. Understanding Fs sets involves recognizing their role in the hierarchy of Borel sets, where they serve as the second level of complexity after closed sets.
Understanding Borel Sets
Borel sets form the smallest s-algebra containing all open sets in a topological space, generated through countable unions, intersections, and complements of open sets. Fs sets represent a specific subclass of Borel sets constructed as countable unions of closed sets, exemplifying the complexity hierarchy within the Borel s-algebra. Understanding Borel sets is crucial in measure theory and real analysis, as they provide the foundation for defining measurable functions and probability measures.
Hierarchical Structure in Borel Sets
Fs sets, defined as countable unions of closed sets, occupy a fundamental position within the Borel hierarchy, specifically at the second level (S^0_2). The Borel hierarchy organizes sets based on operations of countable unions and intersections starting from open sets, with closed, Fs, Gd, and more complex sets ascending this structure. Understanding Fs sets is crucial for analyzing the intricate layers of Borel sets, as they demonstrate how countable operations build complexity in measurable and topological properties.
Key Differences: Fσ Set vs Borel Set
Fs sets are defined as countable unions of closed sets, making them a specific subclass within the broader Borel s-algebra. Borel sets are generated by the s-algebra formed from all open sets, encompassing Fs sets as well as Gd sets (countable intersections of open sets) and many more complex set constructions. The key difference lies in their structural definition and hierarchy: Fs sets have explicit representation via closed sets unions, whereas Borel sets include all sets obtainable from open sets through countable unions, intersections, and complements.
Examples of Fσ Sets
Fs sets are countable unions of closed sets, such as the set of rational numbers expressed as the union of singletons, each being a closed set in the standard topology on the real line. Another example includes the set of all points with rational coordinates in the plane, which is the union of countably many closed sets containing single points. These examples illustrate that every closed set is trivially an Fs set, and countable unions of closed sets, like countable dense subsets, model fundamental Fs sets beyond simple intervals.
Examples of Borel Sets
Borel sets include all open and closed sets in a given topological space, such as intervals like [0,1], (0,1), and their countable unions and intersections. For example, any finite or countable union of closed intervals forms an Fs set, which is a subclass of Borel sets. Complex Borel sets arise by iterating operations of countable union, countable intersection, and complement starting from open sets.
Applications of Fσ and Borel Sets in Analysis
Fs sets, defined as countable unions of closed sets, find crucial applications in real analysis and descriptive set theory, especially in the study of measurable functions and convergence properties. Borel sets, generated from open sets through countable unions, intersections, and complements, form the foundation of Borel sigma-algebras essential for defining Borel measurable functions and constructing probability measures. Both Fs and Borel sets play significant roles in functional analysis, ergodic theory, and measure theory, facilitating the characterization of continuity, integrability, and limit behaviors of functions.
Significance in Measure Theory
Fs sets, formed as countable unions of closed sets, are fundamental in measure theory due to their definability within the Borel hierarchy and their role in approximating more complex measurable sets. Borel sets, generated from open sets via countable unions, intersections, and complements, encompass Fs sets and establish the standard s-algebra on which Lebesgue measure is defined. The significance lies in Fs sets providing a tractable subclass of Borel sets that aid in understanding measurable functions, regularity properties, and the construction of outer measures.
Summary: Comparing Fσ and Borel Sets
Fs sets are countable unions of closed sets and form a subclass within Borel sets, which are generated from open sets through countable unions, intersections, and complements. Every Fs set is a Borel set, but not all Borel sets fall into the Fs category due to the broader operations allowed in their construction. This distinction highlights the layered complexity in the hierarchy of measurable sets in topology and real analysis.
Fσ set Infographic
 libterm.com
libterm.com