Lie groups combine algebraic structures with smooth manifolds, providing a framework for continuous symmetry in mathematics and physics. These groups are instrumental in understanding geometric transformations and differential equations. Discover how Lie groups deepen your grasp of symmetry, topology, and their applications throughout this article.
Table of Comparison
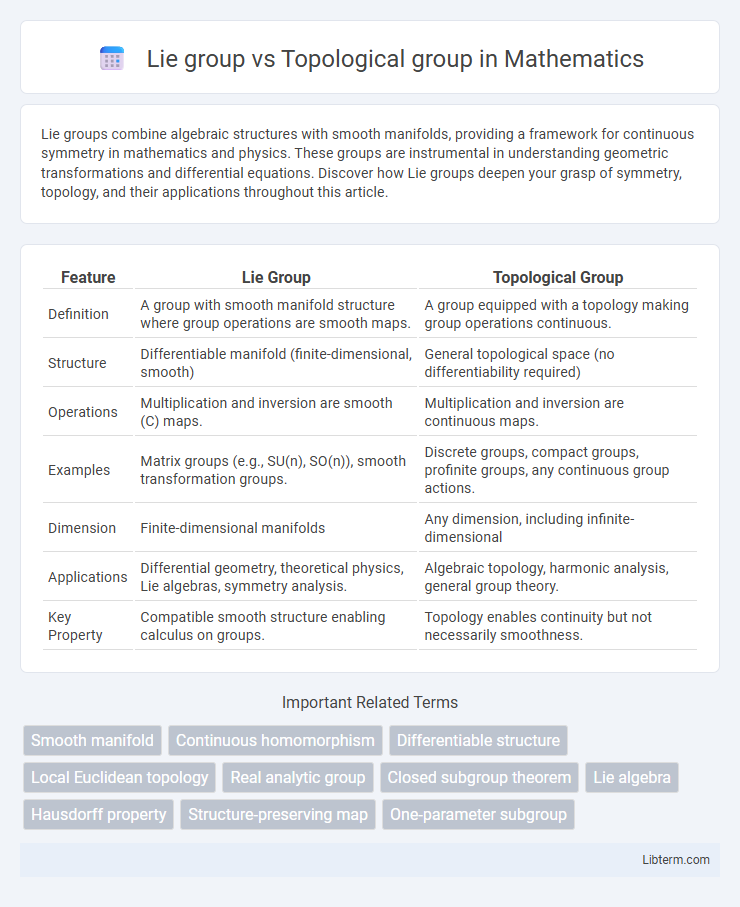
| Feature | Lie Group | Topological Group |
|---|---|---|
| Definition | A group with smooth manifold structure where group operations are smooth maps. | A group equipped with a topology making group operations continuous. |
| Structure | Differentiable manifold (finite-dimensional, smooth) | General topological space (no differentiability required) |
| Operations | Multiplication and inversion are smooth (C) maps. | Multiplication and inversion are continuous maps. |
| Examples | Matrix groups (e.g., SU(n), SO(n)), smooth transformation groups. | Discrete groups, compact groups, profinite groups, any continuous group actions. |
| Dimension | Finite-dimensional manifolds | Any dimension, including infinite-dimensional |
| Applications | Differential geometry, theoretical physics, Lie algebras, symmetry analysis. | Algebraic topology, harmonic analysis, general group theory. |
| Key Property | Compatible smooth structure enabling calculus on groups. | Topology enables continuity but not necessarily smoothness. |
Introduction to Lie Groups and Topological Groups
Lie groups are smooth manifolds equipped with group structures where the group operations are smooth maps, enabling the use of differential geometry in analyzing group properties. Topological groups generalize this concept by combining group theory with topology, requiring only that the group operations be continuous, which allows for broader applications beyond differentiable settings. The study of Lie groups often focuses on finite-dimensional cases with smooth structures, while topological groups encompass a wider variety of examples including infinite-dimensional and non-smooth groups.
Fundamental Definitions
Lie groups are smooth manifolds equipped with group operations that are differentiable, blending algebraic and geometric structures. Topological groups consist of groups endowed with a topology where the group multiplication and inversion are continuous functions, emphasizing continuity over smoothness. The key distinction lies in the requirement for Lie groups to have differentiable maps, whereas topological groups only require continuity, making every Lie group a topological group but not vice versa.
Key Properties of Lie Groups
Lie groups are smooth manifolds equipped with group operations that are differentiable, allowing for the application of calculus on these groups. Key properties include a finite-dimensional structure, the existence of a Lie algebra tangent to the identity element, and smooth exponential maps linking Lie algebras to Lie groups. In contrast, topological groups require only continuous group operations without the differentiable manifold structure essential to Lie groups.
Essential Features of Topological Groups
Topological groups combine algebraic and topological structures through a group equipped with a topology that makes the group operations--multiplication and inversion--continuous. Essential features include the continuity of the map \( (x, y) \mapsto xy^{-1} \) from \( G \times G \) to \( G \), the existence of a neighborhood basis of the identity element consisting of open sets symmetric and stable under group operation, and the homogeneity of the space due to translation invariance. Unlike Lie groups, which require smooth manifold structures and differentiable group operations, topological groups demand only continuity, allowing broader applicability in areas such as harmonic analysis and abstract algebra.
Algebraic Structures: Similarities and Differences
Lie groups and topological groups both combine group theory with topology, but Lie groups have a differentiable manifold structure that enables smooth group operations, while topological groups require only continuity of the group operations. The algebraic structure in Lie groups is tightly connected to their Lie algebra, allowing for linearization and differential analysis, which is absent in general topological groups. Topological groups emphasize continuous symmetries without necessarily possessing the smoothness properties that define Lie groups, leading to differences in structural and analytical methods.
Topological Aspects: Continuity and Smoothness
Topological groups emphasize continuity by requiring the group operations--multiplication and inversion--to be continuous functions relative to the topology defined on the set. Lie groups extend this concept by imposing a smooth manifold structure, ensuring these group operations are not only continuous but infinitely differentiable, enabling the use of calculus techniques. The smoothness condition in Lie groups allows for more refined analysis of group actions, representations, and differential geometry compared to the broader topological continuity in topological groups.
Examples of Lie Groups and Topological Groups
Examples of Lie groups include matrix groups such as the general linear group GL(n, R), the special orthogonal group SO(n), and the unitary group U(n), which are smooth manifolds with group operations compatible with differentiable structures. Topological groups encompass a broader category, including groups like the circle group S^1, the additive group of real numbers R, and the p-adic integers, where the group operations are continuous but not necessarily differentiable. Lie groups form a subset of topological groups distinguished by their smooth manifold properties, while topological groups can lack this differentiable structure yet maintain continuity in their operations.
Applications in Mathematics and Physics
Lie groups, characterized by smooth manifolds with group operations, play a crucial role in differential geometry and theoretical physics, particularly in describing continuous symmetries and conservation laws in quantum mechanics and general relativity. Topological groups, defined by continuity of group operations in a general topological space, provide foundational frameworks for harmonic analysis, representation theory, and ergodic theory, influencing fields like number theory and dynamical systems. The interplay between Lie groups and topological groups enables advanced applications such as gauge theory, particle physics modeling, and the classification of differentiable manifolds.
Choosing the Right Framework: When to Use Which
Lie groups provide a smooth manifold structure combined with group operations, ideal for analyzing continuous symmetry in differential geometry and theoretical physics. Topological groups emphasize continuity without requiring differentiability, making them suitable for studying general group actions and abstract harmonic analysis. Selecting the right framework depends on whether smooth structure and differentiability are essential (Lie groups) or if a broader topological context suffices (topological groups).
Conclusion: Bridging Lie Groups and Topological Groups
Lie groups provide a smooth manifold structure that enhances topological groups by incorporating differentiable operations, enabling applications in geometry and physics. The key bridge lies in the compatibility of continuous group operations with differentiability, allowing Lie groups to serve as finite-dimensional examples of topological groups with rich analytical properties. Understanding this relationship deepens insights into symmetry, group actions, and the seamless integration of algebraic and topological frameworks.
Lie group Infographic
 libterm.com
libterm.com