Matrix algebra involves the study of matrices, which are rectangular arrays of numbers, symbols, or expressions arranged in rows and columns. It encompasses operations such as addition, multiplication, inversion, and finding determinants, essential for solving linear equations and modeling complex systems. Explore the rest of the article to deepen your understanding of how matrix algebra can simplify and solve various mathematical problems.
Table of Comparison
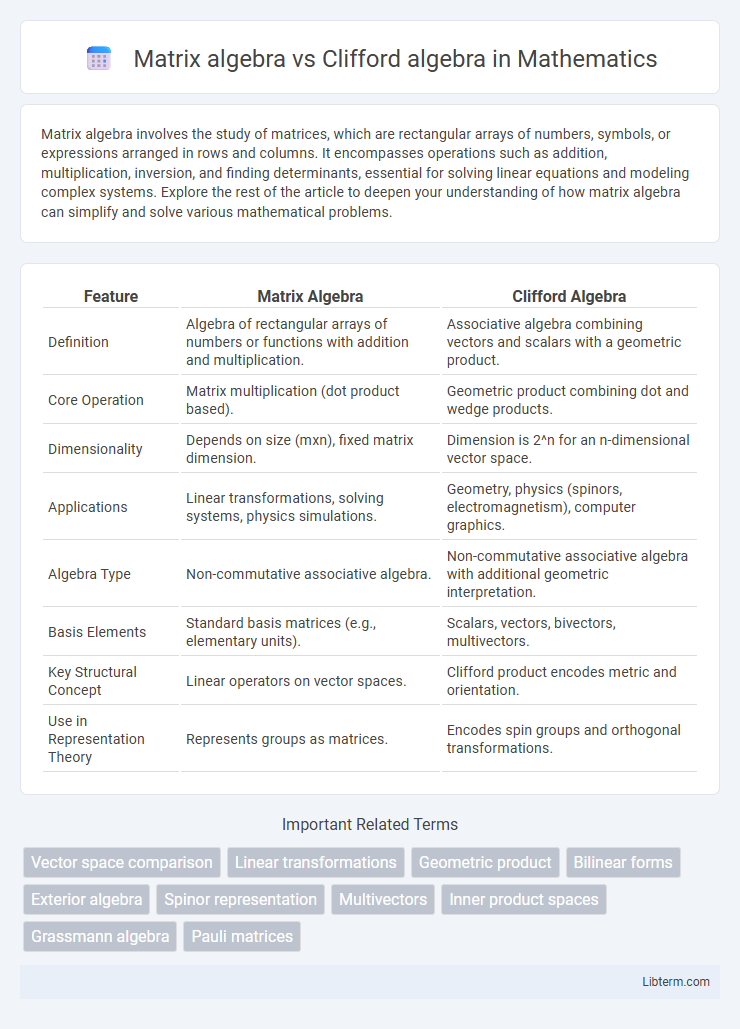
| Feature | Matrix Algebra | Clifford Algebra |
|---|---|---|
| Definition | Algebra of rectangular arrays of numbers or functions with addition and multiplication. | Associative algebra combining vectors and scalars with a geometric product. |
| Core Operation | Matrix multiplication (dot product based). | Geometric product combining dot and wedge products. |
| Dimensionality | Depends on size (mxn), fixed matrix dimension. | Dimension is 2^n for an n-dimensional vector space. |
| Applications | Linear transformations, solving systems, physics simulations. | Geometry, physics (spinors, electromagnetism), computer graphics. |
| Algebra Type | Non-commutative associative algebra. | Non-commutative associative algebra with additional geometric interpretation. |
| Basis Elements | Standard basis matrices (e.g., elementary units). | Scalars, vectors, bivectors, multivectors. |
| Key Structural Concept | Linear operators on vector spaces. | Clifford product encodes metric and orientation. |
| Use in Representation Theory | Represents groups as matrices. | Encodes spin groups and orthogonal transformations. |
Introduction to Matrix Algebra and Clifford Algebra
Matrix algebra involves the study of matrices and their operations, such as addition, multiplication, and inversion, which are fundamental in linear transformations and systems of linear equations. Clifford algebra extends matrix algebra by incorporating geometric concepts, allowing the representation of vectors, multivectors, and transformations within a unified algebraic framework. This extension provides powerful tools for applications in physics, computer graphics, and robotics by enabling efficient manipulation of rotations, reflections, and other geometric transformations.
Historical Background and Evolution
Matrix algebra originated in the mid-19th century through the work of mathematicians like Arthur Cayley and James Joseph Sylvester, who formalized matrices as tools for solving linear equations and transformations. Clifford algebra, introduced by William Kingdon Clifford in the late 19th century, extended these concepts by integrating geometric interpretations with algebraic structures to generalize complex numbers and quaternions. The evolution of Clifford algebra enriched mathematical physics and geometry, providing a unified framework that surpasses matrix algebra in handling multidimensional spaces and transformations.
Fundamental Definitions and Concepts
Matrix algebra involves the manipulation of rectangular arrays of numbers or symbols arranged in rows and columns, focusing on operations such as addition, multiplication, and inversion within linear transformations and vector spaces. Clifford algebra extends these concepts by introducing a unifying framework that blends geometric notions with algebraic structures, capturing elements like vectors, scalars, and higher-grade objects through a graded algebra system defined by the geometric product. Fundamental to Clifford algebra are its basis elements satisfying specific anticommutation relations, enabling the representation of rotations, reflections, and other transformations beyond the capabilities of conventional matrix algebra.
Structure and Dimensions: Comparing the Frameworks
Matrix algebra operates within fixed dimensions defined by the size of matrices, typically involving square arrays of numbers with well-established rules for addition, multiplication, and inversion. Clifford algebra extends beyond matrices by incorporating geometric interpretations and multivector elements, allowing the representation of complex structures like rotations and reflections in various dimensions. The framework of Clifford algebra is dimension-dependent but more flexible, encoding both vector spaces and their metrics, thus providing a richer algebraic structure than traditional matrix algebra.
Operations: Matrix Multiplication vs. Geometric Product
Matrix multiplication involves combining rows and columns to produce a new matrix, focusing on linear transformations and preserving vector space structure. The geometric product in Clifford algebra extends this by blending inner and outer products, encoding rotations, reflections, and scaling in a unified framework. Unlike matrix multiplication, the geometric product captures both magnitude and orientation, enabling more versatile geometric interpretations and efficient computations in physics and computer graphics.
Applications in Physics and Engineering
Matrix algebra provides a foundation for quantum mechanics, control theory, and computer graphics by enabling efficient representation and manipulation of linear transformations and vector spaces. Clifford algebra extends these capabilities by incorporating geometric interpretations, facilitating applications in electromagnetism, relativity, and robotics for modeling rotations and spacetime symmetries. The algebraic framework of Clifford algebra offers compact solutions for complex physical phenomena, surpassing the conventional scope of matrix algebra in multidimensional and geometric contexts.
Representation of Transformations
Matrix algebra represents linear transformations using matrices that operate on vector spaces through standard matrix multiplication, enabling efficient computation and composition of transformations. Clifford algebra generalizes this by encoding geometric transformations such as rotations and reflections within multivectors, providing a unified framework that captures both linear and metric properties of space. This allows Clifford algebra to represent complex transformations compactly and intuitively, often simplifying computations in physics and computer graphics compared to traditional matrix approaches.
Advantages and Limitations of Each Algebra
Matrix algebra offers strong computational efficiency and well-established numerical methods, making it ideal for solving linear systems and transformations in fixed-dimensional vector spaces. Clifford algebra provides a more comprehensive framework that unifies complex numbers, quaternions, and higher-dimensional geometry, facilitating geometric interpretations and operations like rotations and reflections in diverse dimensions. However, matrix algebra can struggle with geometric interpretations beyond linear transformations, while Clifford algebra's complexity and less widespread software support can limit its practical application in standard computational tasks.
Computational Efficiency and Software Support
Matrix algebra offers high computational efficiency due to optimized linear algebra libraries such as BLAS and LAPACK, which enable fast matrix operations on modern hardware and are widely supported across languages like Python, MATLAB, and C++. Clifford algebra provides a richer framework for geometric computations but often incurs higher computational complexity, with fewer specialized libraries available, making implementations less efficient and less common in mainstream software. Software support for Clifford algebra is growing with packages like GAlgebra in Python, but it lacks the extensive optimization and broad adoption enjoyed by matrix algebra in scientific computing and engineering.
Future Trends and Research Directions
Future trends in matrix algebra emphasize the development of high-performance algorithms for large-scale data analysis and quantum computing applications, harnessing advances in parallel processing and machine learning integration. Clifford algebra research is increasingly focused on geometric computing, robotics, and theoretical physics, aiming to unify algebraic frameworks for multidimensional data and spacetime modeling. Emerging directions also include hybrid approaches combining matrix and Clifford algebra techniques to enhance computational efficiency and dimensional insights in complex systems.
Matrix algebra Infographic
 libterm.com
libterm.com