A representable functor is a fundamental concept in category theory that assigns to each object in a category a set of morphisms into a fixed object, capturing essential structural information. This functor provides a bridge between abstract categories and concrete sets, enabling deep insights into the nature of mathematical objects. Explore the rest of the article to understand how representable functors shape modern mathematical frameworks and their applications.
Table of Comparison
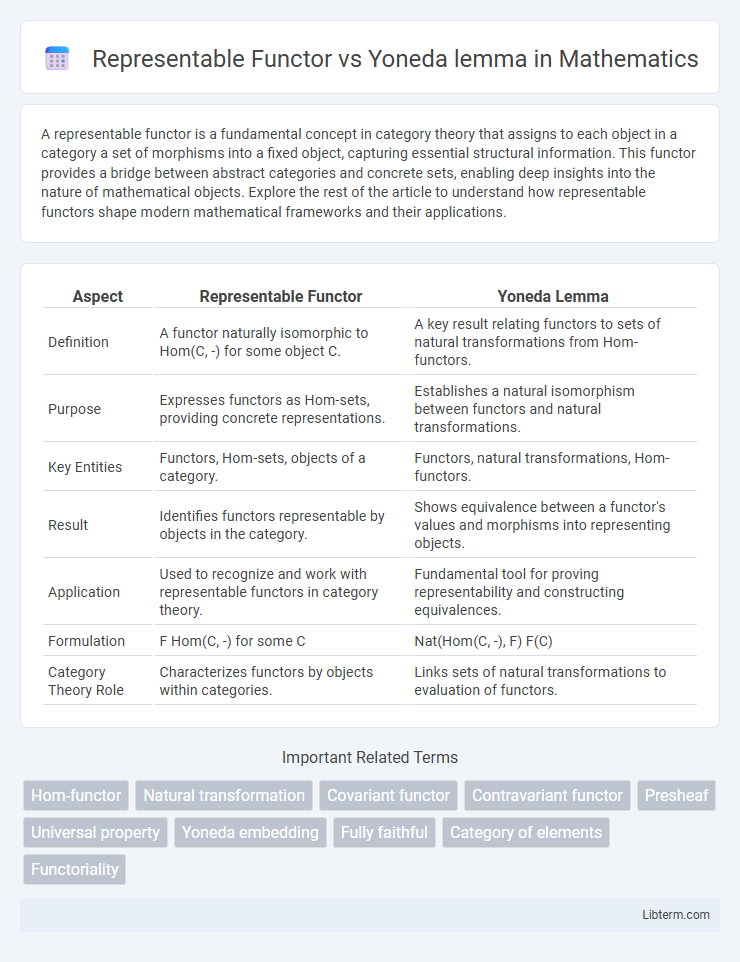
| Aspect | Representable Functor | Yoneda Lemma |
|---|---|---|
| Definition | A functor naturally isomorphic to Hom(C, -) for some object C. | A key result relating functors to sets of natural transformations from Hom-functors. |
| Purpose | Expresses functors as Hom-sets, providing concrete representations. | Establishes a natural isomorphism between functors and natural transformations. |
| Key Entities | Functors, Hom-sets, objects of a category. | Functors, natural transformations, Hom-functors. |
| Result | Identifies functors representable by objects in the category. | Shows equivalence between a functor's values and morphisms into representing objects. |
| Application | Used to recognize and work with representable functors in category theory. | Fundamental tool for proving representability and constructing equivalences. |
| Formulation | F Hom(C, -) for some C | Nat(Hom(C, -), F) F(C) |
| Category Theory Role | Characterizes functors by objects within categories. | Links sets of natural transformations to evaluation of functors. |
Introduction to Representable Functors
Representable functors are a fundamental concept in category theory that link objects in a category to sets of morphisms, providing a concrete way to study abstract structures. They arise when a functor is naturally isomorphic to the Hom-functor for a particular object, revealing deep connections between objects and morphisms. The Yoneda lemma formalizes this relationship by stating that every natural transformation from a representable functor to any other functor corresponds uniquely to an element of the target functor evaluated at the representing object.
Understanding the Yoneda Lemma
The Yoneda Lemma establishes a fundamental correspondence between natural transformations from a representable functor Hom(C, -) to any functor F and the elements of F(C), emphasizing how objects in a category are fully characterized by the morphisms they admit. Representable functors serve as key examples within this framework, encoding objects via hom-sets, allowing the embedding of a category into a functor category and enabling a deeper understanding of categorical structures through natural transformations. Understanding the Yoneda Lemma illuminates how representable functors provide a powerful tool for analyzing and reconstructing objects using universal properties and naturality conditions.
Defining Representable Functors in Category Theory
Representable functors in category theory are defined as functors naturally isomorphic to the hom-functor Hom_C(A, -) for some object A in a category C. This definition links each representable functor to a specific object and captures morphisms from that object, facilitating concrete analysis within abstract categorical structures. The Yoneda lemma leverages representable functors to establish a natural isomorphism between natural transformations from Hom_C(A, -) to any functor F and elements of F(A), highlighting the foundational role of representable functors in categorical reasoning.
The Statement and Intuition Behind the Yoneda Lemma
The Yoneda lemma states that for any locally small category \( \mathcal{C} \) and any functor \( F: \mathcal{C} \to \mathbf{Set} \), the set of natural transformations from the representable functor \( \hom_\mathcal{C}(C, -) \) to \( F \) is naturally isomorphic to \( F(C) \). This correspondence reveals that a representable functor fully captures the behavior of an object \( C \) via morphisms originating from \( C \), linking representability to natural transformations. Intuitively, the Yoneda lemma formalizes how each object in a category can be understood completely by its relationships (morphisms) with other objects, providing a bridge between objects and functors.
Relationship Between Representable Functors and Yoneda Lemma
Representable functors are those naturally isomorphic to Hom-functors, embodying objects within a category through morphisms. The Yoneda lemma establishes a fundamental equivalence between elements of a functor and natural transformations from representable functors, providing a powerful tool to analyze functor behavior. This relationship reveals that every functor can be fully understood via its interactions with representable functors, highlighting the central role of the Yoneda lemma in category theory.
Examples of Representable Functors
Representable functors are those naturally isomorphic to the Hom-functor Hom_C(A, -) for some object A in a category C, providing concrete examples like the functor assigning each vector space V its dual space Hom(V, K). The Yoneda lemma establishes a natural isomorphism between natural transformations from Hom_C(A, -) to any functor F and the elements of F(A), showing how representable functors encode objects via morphisms. Classic examples include the functor Hom_Set(X, -) represented by a set X, illustrating how representable functors realize objects through their mapping properties in categories such as Set, Top, or Mod.
Practical Applications of the Yoneda Lemma
The Yoneda lemma is a foundational tool in category theory that allows the representation of any functor by a set of morphisms, making it essential for understanding representable functors. It facilitates practical applications such as simplifying complex natural transformations, aiding in the characterization of algebraic structures, and enabling efficient computation in functional programming languages. By leveraging the Yoneda lemma, developers and mathematicians can transform abstract categorical concepts into concrete, computable objects, enhancing modularity and code reuse.
Proving the Yoneda Lemma Step-by-Step
The Yoneda Lemma establishes a natural isomorphism between the set of natural transformations from the hom-functor \( \text{Hom}(A, -) \) to any functor \( F \) and the set \( F(A) \) itself, fundamentally linking representable functors with elements of \( F \). To prove the lemma, start by defining a map that assigns to each natural transformation \( \eta \) the element \( \eta_A(\text{id}_A) \in F(A) \), then demonstrate this correspondence is both injective and surjective by verifying naturality and inverse construction. This step-by-step proof highlights why representable functors, characterized by hom-sets, serve as a cornerstone in category theory, illuminating functor behavior through concrete elements.
Significance of Representability in Category Theory
Representable functors serve as a fundamental bridge in category theory by translating abstract categorical structures into concrete sets through the Yoneda lemma, which states a natural isomorphism between hom-sets and natural transformations. The significance of representability lies in its ability to characterize objects entirely by their relationships to other objects, facilitating a deeper understanding of morphisms and natural transformations. This concept underpins many core results and constructions in category theory, enabling the simplification and classification of complex categorical phenomena.
Comparing Representable Functor and Yoneda Lemma: Key Takeaways
Representable functors are specific functors naturally isomorphic to hom-functors, providing concrete examples within category theory, while the Yoneda lemma offers a general isomorphism that characterizes all functors by their action on hom-sets. Key takeaways include that representable functors serve as foundational objects allowing categories to be embedded into functor categories, and the Yoneda lemma guarantees that each object in a category can be fully understood by the natural transformations from its hom-functor. The lemma thus bridges representable functors and all functors, highlighting the representability condition as a means to analyze categorical structures through functorial perspectives.
Representable Functor Infographic
 libterm.com
libterm.com