The Hom functor is a fundamental concept in category theory that assigns to each pair of objects the set of morphisms between them, capturing the structure-preserving relationships in a category. It is crucial in defining natural transformations and in the study of representable functors, providing deep insights into the nature of mathematical objects. Explore the rest of this article to understand how the Hom functor shapes modern algebra and beyond.
Table of Comparison
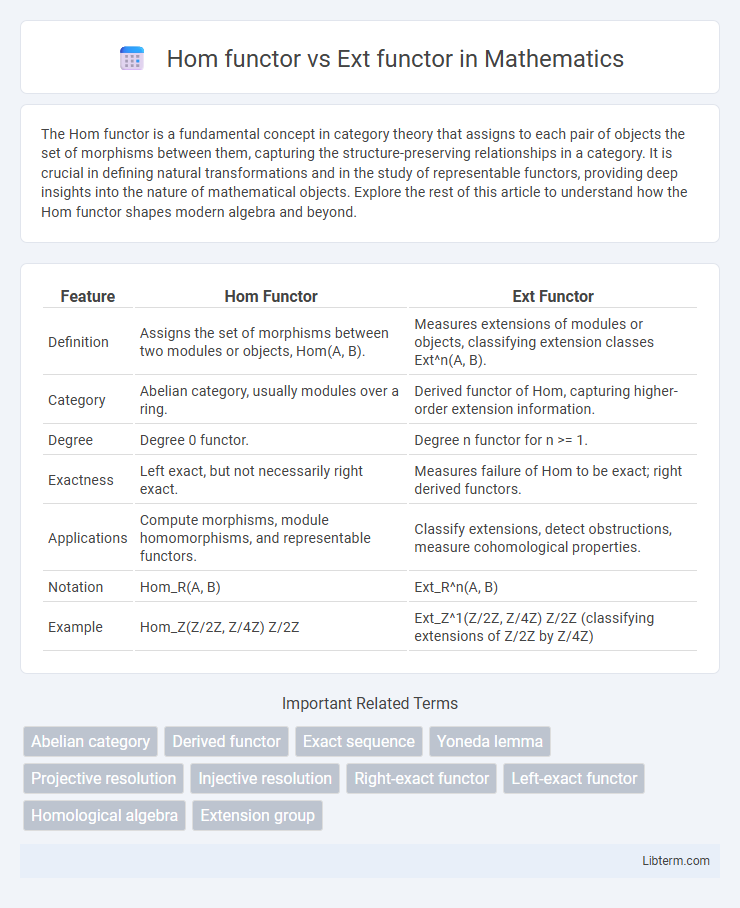
| Feature | Hom Functor | Ext Functor |
|---|---|---|
| Definition | Assigns the set of morphisms between two modules or objects, Hom(A, B). | Measures extensions of modules or objects, classifying extension classes Ext^n(A, B). |
| Category | Abelian category, usually modules over a ring. | Derived functor of Hom, capturing higher-order extension information. |
| Degree | Degree 0 functor. | Degree n functor for n >= 1. |
| Exactness | Left exact, but not necessarily right exact. | Measures failure of Hom to be exact; right derived functors. |
| Applications | Compute morphisms, module homomorphisms, and representable functors. | Classify extensions, detect obstructions, measure cohomological properties. |
| Notation | Hom_R(A, B) | Ext_R^n(A, B) |
| Example | Hom_Z(Z/2Z, Z/4Z) Z/2Z | Ext_Z^1(Z/2Z, Z/4Z) Z/2Z (classifying extensions of Z/2Z by Z/4Z) |
Introduction to Hom and Ext Functors
The Hom functor, denoted as Hom(A, -), maps objects in an abelian category to sets of morphisms, capturing the structure-preserving transformations between modules or objects. The Ext functor, Ext^n(A, -), generalizes this by measuring the extent to which exact sequences fail to split, thus classifying extensions of modules and providing higher-dimensional cohomological information. Together, these functors form the foundation of homological algebra, linking morphisms and extensions to analyze module and category structures comprehensively.
Definitions: Hom Functor Explained
The Hom functor assigns to each pair of modules \( (M, N) \) the set of module homomorphisms \(\text{Hom}(M, N)\), capturing morphisms within abelian categories or module categories. As a covariant functor in the second argument and contravariant in the first, \(\text{Hom}(-, N)\) and \(\text{Hom}(M, -)\) preserve exactness properties crucial to defining derived functors. Unlike the Ext functor, which measures extensions and higher derived functors of Hom, the Hom functor itself computes direct morphisms without extension data.
Definitions: Ext Functor Explained
The Ext functor, denoted as Ext^n(A, B), measures the extent to which an abelian group or module B fails to be projective relative to A through derived functors of the Hom functor. Unlike Hom, which calculates morphisms between modules, Ext captures extensions and classifies exact sequences involving A and B, revealing deeper homological relationships. Ext functors are central in homological algebra, providing insights into module extensions, obstructions, and derived category structures beyond the direct morphism analysis by Hom.
Hom Functor: Key Properties and Examples
The Hom functor, denoted as Hom(-,B) or Hom(A,-), is a covariant or contravariant functor from the category of modules (or vector spaces) to the category of abelian groups, capturing morphisms between objects. It is right exact, preserving epimorphisms but generally not exact, which contrasts with the Ext functor that measures the failure of exactness of Hom. Typical examples include Hom(Z, A) is isomorphic to A for abelian groups, and Hom(R^n, R^m) corresponds to the space of mxn matrices over a ring R, demonstrating its role in morphism classification and module theory.
Ext Functor: Key Properties and Examples
The Ext functor, derived from the Hom functor, measures extensions between modules and provides crucial insight into their extension classes, capturing higher-dimensional cohomological information. Key properties include its role in classifying extensions, exactness conditions, and its computation through projective or injective resolutions, with Ext^1 representing equivalence classes of module extensions. Examples such as Ext^n_Z(Z/mZ,Z) illustrate torsion phenomena in abelian groups, while Ext functors in homological algebra reveal obstructions and deformation properties in module theory.
Comparing Hom and Ext Functors: Similarities
Hom and Ext functors both arise from the category of modules and measure morphism-related properties, but while Hom captures direct morphisms between modules, Ext quantifies extensions and higher derived relationships. Both functors are additive and covariant in one argument while contravariant in the other, providing a framework to analyze module extensions and homological dimensions. Their interplay reveals essential structural information in homological algebra and representation theory, highlighting the depth of module interactions beyond mere morphisms.
Crucial Differences Between Hom and Ext Functors
Hom functor maps a pair of modules to the abelian group of homomorphisms, capturing direct morphisms between objects in categories such as R-modules. Ext functor, as a derived functor of Hom, measures the extent to which modules fail to be projective or injective, providing information about extensions and higher-dimensional cohomological structures. While Hom detects morphisms, Ext reveals obstructions and extension classes, crucial for understanding module extensions, projective resolutions, and derived category theory.
Applications of Hom Functor in Algebra
The Hom functor plays a critical role in algebra by measuring morphisms between modules, enabling the study of module homomorphisms, tensor products, and exact sequences. It is fundamental in defining natural transformations, characterizing projective and injective modules, and constructing derived functors such as Ext and Tor. Applications include determining splitting of exact sequences, analyzing module categories, and facilitating duality theories in homological algebra.
Applications of Ext Functor in Homological Algebra
The Ext functor measures extensions and classifies equivalence classes of module extensions, playing a crucial role in detecting and analyzing obstructions to splitting exact sequences in homological algebra. It is extensively used in representation theory and group cohomology to study extensions of modules and to compute derived functors of Hom, revealing hidden structure in complex algebraic objects. Unlike the Hom functor, which captures morphisms between modules, the Ext functor quantifies higher-order relationships and detects nontrivial extensions, facilitating calculations involving projective and injective resolutions.
Summary: When to Use Hom vs Ext Functors
The Hom functor measures morphisms between modules, capturing direct mappings and their structure, making it ideal for analyzing module homomorphisms and exact sequences. The Ext functor extends this by classifying extensions and capturing higher-dimensional cohomological information, essential for detecting obstructions to splitting short exact sequences and exploring module extensions. Use Hom for direct morphism characterization and Ext for understanding extension classes and derived functor phenomena in homological algebra.
Hom functor Infographic
 libterm.com
libterm.com