Periodic patterns play a crucial role in various fields, from mathematics and physics to computer science and art, by revealing recurring structures and behaviors that simplify complex problems. Understanding these patterns helps you identify predictable cycles and optimize processes efficiently. Explore the rest of the article to discover how periodicity impacts different domains and practical applications.
Table of Comparison
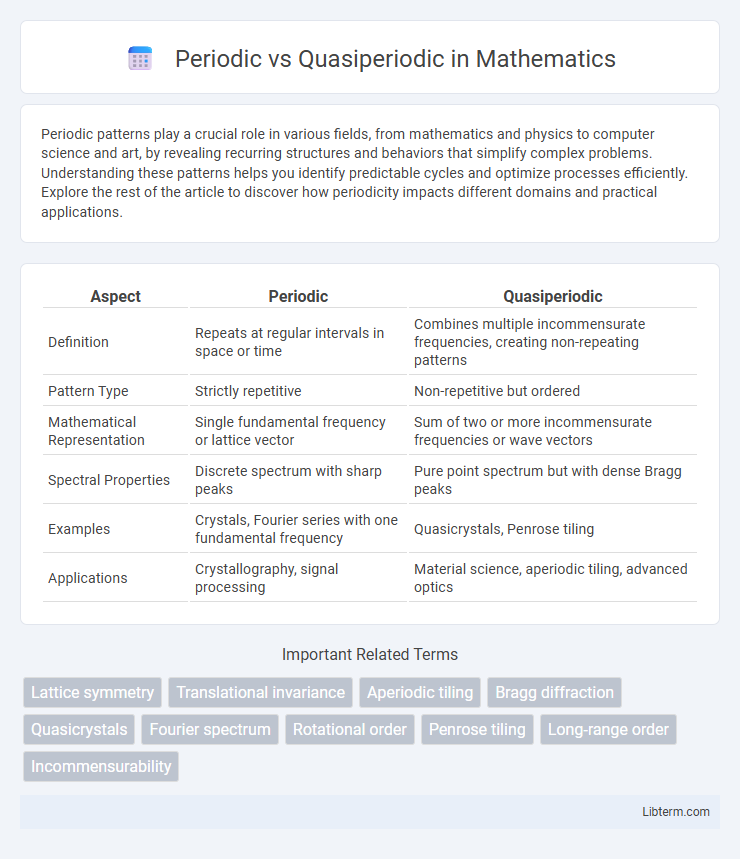
| Aspect | Periodic | Quasiperiodic |
|---|---|---|
| Definition | Repeats at regular intervals in space or time | Combines multiple incommensurate frequencies, creating non-repeating patterns |
| Pattern Type | Strictly repetitive | Non-repetitive but ordered |
| Mathematical Representation | Single fundamental frequency or lattice vector | Sum of two or more incommensurate frequencies or wave vectors |
| Spectral Properties | Discrete spectrum with sharp peaks | Pure point spectrum but with dense Bragg peaks |
| Examples | Crystals, Fourier series with one fundamental frequency | Quasicrystals, Penrose tiling |
| Applications | Crystallography, signal processing | Material science, aperiodic tiling, advanced optics |
Understanding Periodic Patterns
Periodic patterns exhibit a consistent and repeating structure at fixed intervals, characterized by their exact repetition over time or space, making them predictable and easy to analyze using Fourier series or wavelet transforms. Understanding periodic patterns involves identifying their fundamental frequency and harmonics, which helps in signal processing, time series analysis, and pattern recognition applications. In contrast, quasiperiodic patterns contain multiple incommensurate frequencies, resulting in complex, non-repetitive patterns that cannot be represented by a single fundamental period.
What Defines Quasiperiodic Structures?
Quasiperiodic structures are defined by their ordered yet non-repetitive arrangement, characterized by patterns that never exactly repeat but exhibit long-range order. Unlike periodic structures, which have translational symmetry and a repeating unit cell, quasiperiodic patterns combine multiple incommensurate wavelengths, resulting in a fractal-like spatial organization. These structures are exemplified in quasicrystals where atomic arrangements display symmetries forbidden in periodic crystals, such as fivefold rotational symmetry.
Key Differences Between Periodic and Quasiperiodic
Periodic systems exhibit repeating patterns with a fixed interval, characterized by a single fundamental frequency or its harmonics. Quasiperiodic systems combine two or more incommensurate frequencies, leading to patterns that never exactly repeat but maintain a structured order. The key difference lies in periodicity: periodic systems have strictly repeating cycles, while quasiperiodic systems display complex, non-repeating oscillations with ordered frequency components.
Mathematical Foundations of Periodicity
Periodic functions exhibit exact repetition at fixed intervals defined by a fundamental period, inherently linked to integer multiples of this base period within their mathematical structure. Quasiperiodic functions combine two or more incommensurate frequencies, creating patterns that never exactly repeat yet display continuous oscillatory behavior described by sums of periodic components with irrational frequency ratios. The mathematical foundations of periodicity rely on Fourier series representations for periodic functions, while quasiperiodicity involves Fourier quasi-series or generalized harmonic analysis on higher-dimensional tori emphasizing non-integer frequency relationships.
Quasiperiodicity in Nature and Science
Quasiperiodicity in nature is observed in complex systems such as quasicrystals, biological rhythms, and certain astronomical phenomena, where patterns repeat without exact periodicity but maintain long-range order. Scientific studies reveal that quasiperiodic structures exhibit unique properties, including non-repetitive symmetry and fractal-like behavior, which influence material strength, electronic conductivity, and ecological cycles. Understanding quasiperiodicity advances fields like crystallography, meteorology, and mathematical physics by explaining behaviors that periodic models cannot accurately capture.
Applications of Periodic Arrangements
Periodic arrangements in materials science enable precise control over electronic, optical, and mechanical properties, making them essential in semiconductor device fabrication and photonic crystal development. These structures facilitate bandgap engineering critical for laser diodes, solar cells, and sensors by ensuring uniformity and predictability at the atomic or molecular scale. Their predictable symmetry and repeatability are exploited in nanotechnology and metamaterials to enhance conductivity, magnetism, and light manipulation capabilities.
Unique Properties of Quasiperiodic Materials
Quasiperiodic materials exhibit unique atomic arrangements that lack translational symmetry yet maintain long-range order, distinguishing them from periodic crystals. Their aperiodic patterning results in unusual electronic and thermal properties, such as non-repeating diffraction patterns and anomalous conductivity. These materials often demonstrate enhanced mechanical strength and low friction coefficients, making them valuable in advanced engineering applications.
Identifying Periodic vs. Quasiperiodic in Real Data
Identifying periodic versus quasiperiodic signals in real data involves analyzing frequency components through spectral methods such as Fourier Transform and wavelet analysis. Periodic signals exhibit discrete, well-defined frequency peaks corresponding to a single fundamental frequency and its harmonics, whereas quasiperiodic signals display multiple incommensurate frequencies without exact harmonic relationships. Time-frequency analysis and phase space reconstruction techniques help distinguish quasiperiodic behavior by revealing complex oscillatory patterns and non-integer frequency ratios in observational datasets.
Challenges in Analyzing Quasiperiodic Systems
Quasiperiodic systems exhibit non-repeating patterns that complicate their mathematical modeling and numerical simulations compared to periodic systems, which have fixed, repeating intervals. The lack of a single fundamental frequency in quasiperiodic systems leads to challenges in spectral analysis, requiring advanced tools like Fourier transform extensions and time-frequency analysis methods. Furthermore, predicting long-term behavior and stability in quasiperiodic dynamics demands sophisticated algorithms due to their sensitive dependence on initial conditions and multi-frequency interactions.
Future Research and Innovations in Pattern Analysis
Future research in pattern analysis will emphasize developing advanced algorithms capable of distinguishing between periodic and quasiperiodic signals more accurately, leveraging machine learning and nonlinear dynamics. Innovations will target applications in fields such as climate modeling, neuroscience, and materials science, where understanding subtle variations in patterns is crucial. Enhanced computational models and real-time data processing techniques will enable more precise prediction and control of complex systems exhibiting quasiperiodic behavior.
Periodic Infographic
 libterm.com
libterm.com