Cofinite sets are key concepts in set theory, defined as sets whose complements are finite. Understanding cofinite sets helps to grasp foundational ideas in topology and mathematical analysis, where they often appear in discussions about convergence and limit points. Explore the rest of the article to deepen your knowledge of cofinite sets and their applications in mathematics.
Table of Comparison
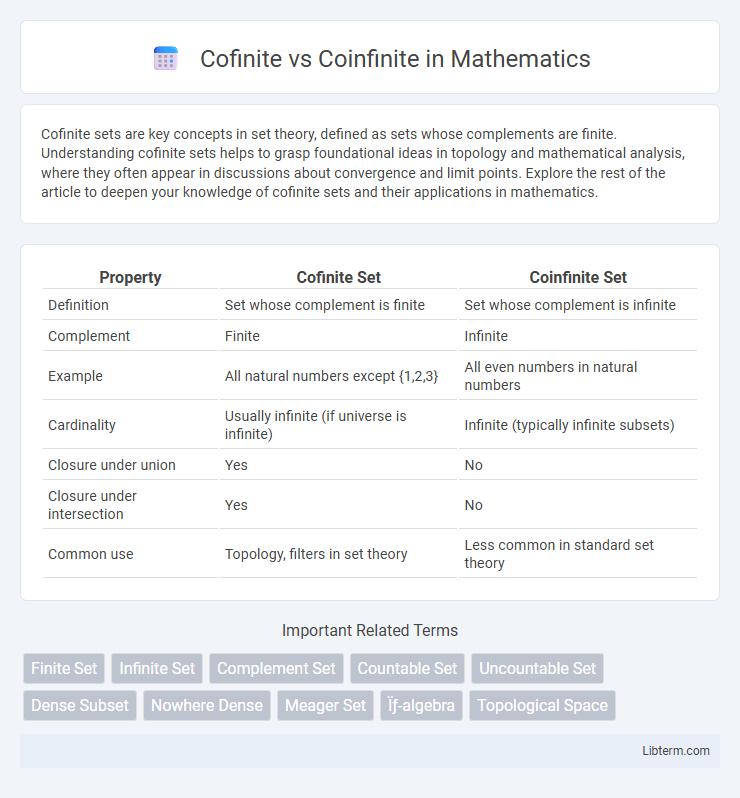
| Property | Cofinite Set | Coinfinite Set |
|---|---|---|
| Definition | Set whose complement is finite | Set whose complement is infinite |
| Complement | Finite | Infinite |
| Example | All natural numbers except {1,2,3} | All even numbers in natural numbers |
| Cardinality | Usually infinite (if universe is infinite) | Infinite (typically infinite subsets) |
| Closure under union | Yes | No |
| Closure under intersection | Yes | No |
| Common use | Topology, filters in set theory | Less common in standard set theory |
Introduction to Cofinite and Coinfinite
Cofinite sets are subsets of a given universal set whose complements are finite, commonly used in topology and set theory due to their role in defining cofinite topology. Coinfinite sets, conversely, have infinite complements, making their properties crucial in understanding density and size comparisons in infinite sets. Understanding cofinite and coinfinite distinctions aids in grasping concepts related to infinite cardinalities and complementarity in mathematical analysis.
Definitions: What Are Cofinite and Coinfinite Sets?
Cofinite sets are defined as subsets of a given universal set whose complements are finite, meaning they contain all elements except for a finite number of them. Coinfinite sets, on the other hand, are those subsets whose complements are infinite, so neither the set nor its complement is finite. Understanding the distinction between cofinite and coinfinite sets is crucial in fields like topology and set theory, where these concepts help classify and analyze infinite structures.
Historical Background and Mathematical Context
Cofinite and coinfinite sets originate from set theory, crucial in analyzing infinite structures and their complements within mathematical logic. Cofinite sets include all but finitely many elements of a given universe, emphasizing finite exceptions, while coinfinite sets have complements that are infinite, highlighting more complex infinite behaviors. These concepts are foundational in topology, combinatorics, and measure theory, illustrating different ways infinity interacts with set complements historically developed through the study of infinite cardinalities and their properties.
Properties of Cofinite Sets
Cofinite sets are defined by having complements in a universal set that are finite, making them significant in topology where they form a cofinite topology on infinite sets. Their key properties include closure under finite intersections and that every superset of a cofinite set is also cofinite, establishing them as filters in set theory. Unlike coinfinite sets, which may have infinite complements, cofinite sets ensure a finite complement, facilitating analysis in convergence and compactness within infinite domains.
Properties of Coinfinite Sets
Coinfinite sets are defined as subsets of a universal set whose complements are finite, meaning their complement contains only a limited number of elements. These sets exhibit properties such as closure under finite intersections and unions, making their algebraic structure well-behaved in set theory. Coinfinite sets often appear in topology and logic, illustrating important examples of co-countable or co-finite topologies.
Key Differences Between Cofinite and Coinfinite
Cofinite sets are defined as those whose complements in a given universal set are finite, meaning they contain almost all elements except a finite number, while coinfinite sets have infinite complements, implying their complements are neither finite nor empty. The key difference lies in the size of the complements: cofinite complements are finite, facilitating properties like closure under finite intersections, whereas coinfinite complements are infinite, affecting their behavior in set operations and topological contexts. Understanding these distinctions is crucial in fields like topology and set theory, where they influence concepts such as convergence, closure, and filter bases.
Examples of Cofinite and Coinfinite Sets
A cofinite set is a subset of a given set whose complement is finite, such as the set of all natural numbers except for a finite number of elements like {1, 2, 3}, exemplified by the set of natural numbers excluding {1, 2, 3}. A coinfinite set, by contrast, has both the subset and its complement being infinite, for example, the set of even natural numbers, where neither the even numbers nor the odd numbers are finite. Understanding cofinite and coinfinite sets is essential in set theory and topology due to their distinct properties regarding finiteness and infiniteness.
Applications in Topology and Algebra
Cofinite sets, defined by having finite complements, play a crucial role in topology by generating the cofinite topology, which models T1 spaces and aids in understanding convergence and continuity properties. Coinfinite sets, typically those with infinite complements, are important in algebra for constructing ideals and filters, influencing the structure of modules and rings through concepts like cofinite submodules. The interplay between cofinite and coinfinite sets facilitates the study of compactness, separability, and finiteness conditions in both topological spaces and algebraic systems.
Cofinite and Coinfinite in Real Analysis
Cofinite sets in real analysis are subsets of real numbers whose complements are finite, meaning they contain all but finitely many elements of a given set, commonly used in topology to define particular types of closed sets. Coinfinite sets, conversely, have infinite complements, making them significant in understanding dense subsets and limit points within real analysis. The interplay between cofinite and coinfinite sets helps characterize the structure of measurable and topological spaces, particularly in the study of convergence and continuity.
Summary and Conclusion
Cofinite sets are the complements of finite sets, containing all elements of a universal set except for a limited number, while coinfinite sets have complements that are infinite yet not encompassing the entire universal set. Understanding the distinction between cofinite and coinfinite sets is critical in fields such as topology and set theory, where the concept of finiteness and infiniteness plays a foundational role. The practical differentiation lies in the size and nature of their complements, influencing their applications in mathematical analysis and theoretical computer science.
Cofinite Infographic
 libterm.com
libterm.com