Geometric complement refers to the set of points or shapes that complete a given geometric figure within a specified space, often used in understanding spatial relationships and properties. It plays a crucial role in fields such as topology, geometry, and computer graphics by helping to define boundaries and excluded areas. Discover how grasping the concept of geometric complement can enhance Your spatial reasoning by reading the full article.
Table of Comparison
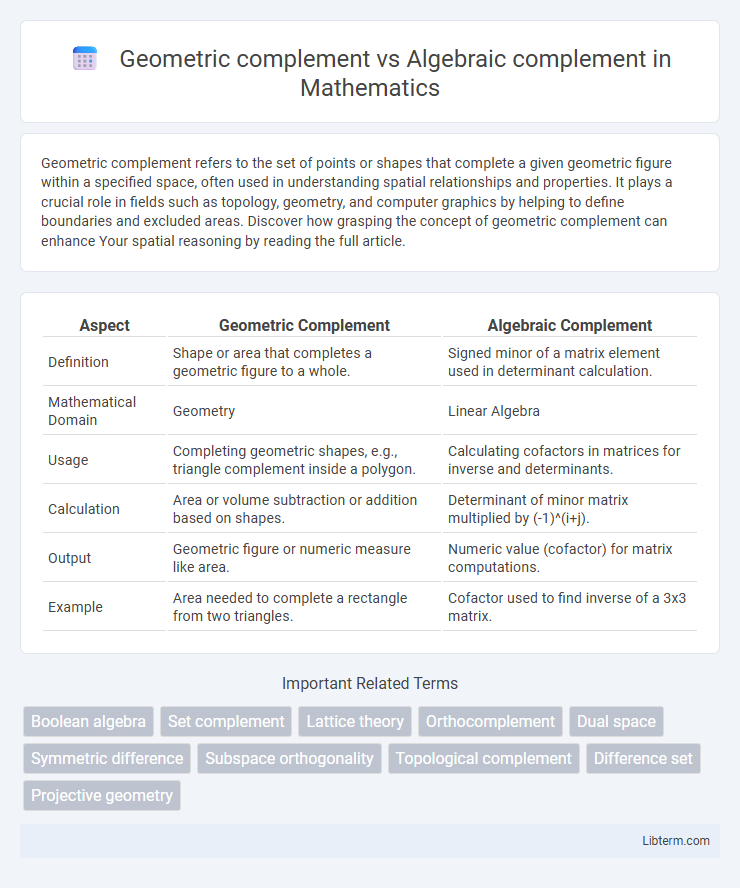
| Aspect | Geometric Complement | Algebraic Complement |
|---|---|---|
| Definition | Shape or area that completes a geometric figure to a whole. | Signed minor of a matrix element used in determinant calculation. |
| Mathematical Domain | Geometry | Linear Algebra |
| Usage | Completing geometric shapes, e.g., triangle complement inside a polygon. | Calculating cofactors in matrices for inverse and determinants. |
| Calculation | Area or volume subtraction or addition based on shapes. | Determinant of minor matrix multiplied by (-1)^(i+j). |
| Output | Geometric figure or numeric measure like area. | Numeric value (cofactor) for matrix computations. |
| Example | Area needed to complete a rectangle from two triangles. | Cofactor used to find inverse of a 3x3 matrix. |
Introduction to Complements in Mathematics
Geometric complements refer to the portion of a figure that completes a shape to a whole, often seen in angles where two angles sum to 90 degrees, forming complementary angles. Algebraic complements, also known as cofactors, are elements used in matrix theory for calculating determinants and inverses, defined by removing a row and column from a matrix and applying a sign factor. Understanding these complements is fundamental in mathematics as they provide essential tools for solving problems in geometry and linear algebra.
Defining Geometric Complement
The geometric complement refers to the vector obtained by subtracting a projection of a vector onto a subspace from the original vector, representing the component orthogonal to that subspace. It is defined as the difference between the original vector and its geometric projection, emphasizing orthogonality in Euclidean space. This contrasts with the algebraic complement, which is based on matrix cofactors and determinants rather than vector orthogonality.
Understanding Algebraic Complement
Algebraic complement refers to the signed cofactor of a matrix element, used in determining the matrix inverse and calculating determinants through cofactor expansion. Unlike the geometric complement, which deals with subspaces and orthogonal complements, the algebraic complement incorporates the sign factor (-1)^(i+j) to account for the element's position, ensuring accurate matrix operations. Understanding algebraic complements is essential for solving linear systems and performing matrix decomposition efficiently.
Key Differences Between Geometric and Algebraic Complements
Geometric complement refers to the portion of a geometric figure that, when combined with a given part, completes the whole shape, often used in angle or area calculations. Algebraic complement, also known as the cofactor in matrix theory, involves a signed minor that plays a crucial role in determinants and matrix inverses. The key difference lies in their applications: geometric complements pertain to spatial or shape-related problems, whereas algebraic complements are fundamental in linear algebra for solving systems of equations and matrix operations.
Applications of Geometric Complement
Geometric complements find extensive applications in computer graphics and computational geometry, where they help calculate areas and volumes by subtracting shapes or defining voids within solids. They are crucial in engineering for structural analysis and in geographic information systems (GIS) for spatial data modeling and land parcel mapping. Unlike algebraic complements, which are primarily used in matrix theory and linear algebra for calculating cofactors and determinants, geometric complements provide spatial and visual insights essential for modeling and simulation tasks.
Applications of Algebraic Complement
Algebraic complements, also known as cofactors, play a crucial role in matrix theory applications such as calculating determinants, finding inverses of matrices, and solving linear systems through Cramer's rule. This concept is extensively used in engineering fields for stability analysis and control system design, where matrix inversion is essential. Geometric complements, contrastingly, relate more to spatial interpretations but have less direct computational applications than algebraic complements in linear algebra.
Visual Representation: Geometric vs Algebraic Complement
The geometric complement is visually represented as the area or region that completes a shape within a given space, often shown as the shaded portion outside a subset in a Venn diagram or geometric figure. In contrast, the algebraic complement involves matrices, where the algebraic complement (cofactor) relates to the minor of an element with an associated sign, usually displayed in determinant expansions or matrix adjugates. This distinction highlights how geometric complements emphasize spatial intuition and area, while algebraic complements focus on numeric calculations and matrix transformations.
Theoretical Importance in Mathematical Problem Solving
Geometric complement and algebraic complement both hold significant theoretical importance in mathematical problem solving, particularly within linear algebra and geometry. The geometric complement relates to spatial intuition in vector spaces and subspace orthogonality, aiding in understanding projections and decompositions. The algebraic complement, tied to cofactors and minors in matrix theory, is crucial for computing determinants and inverses, fundamental in solving linear systems and eigenvalue problems.
Common Mistakes and Misconceptions
Confusing the geometric complement, which involves visualizing shapes and angles in a plane, with the algebraic complement, defined through matrix cofactors and determinants, leads to common mistakes in problem-solving. Students often misinterpret geometric complement as a numerical value rather than a spatial relationship, while algebraic complement errors arise from incorrectly calculating minors and overlooking sign patterns in cofactor matrices. Clarifying these distinctions prevents errors in both geometry and linear algebra applications, ensuring accurate interpretations and computations.
Conclusion: Choosing the Right Complement Method
Selecting the appropriate complement method depends on the context and the nature of the mathematical problem, as geometric complements offer visual intuition while algebraic complements provide precise numerical solutions. Geometric complement is ideal for spatial analysis and problems involving shapes or angles, enhancing conceptual understanding. Algebraic complement suits algebraic equations and matrix calculations where exact values and systematic computation are crucial for accuracy and efficiency.
Geometric complement Infographic
 libterm.com
libterm.com