Choosing the right product ensures you receive the best value and quality tailored to your needs. Understanding key features and benefits helps make an informed decision that suits your lifestyle. Explore the rest of the article to discover expert tips and detailed insights on selecting your ideal product.
Table of Comparison
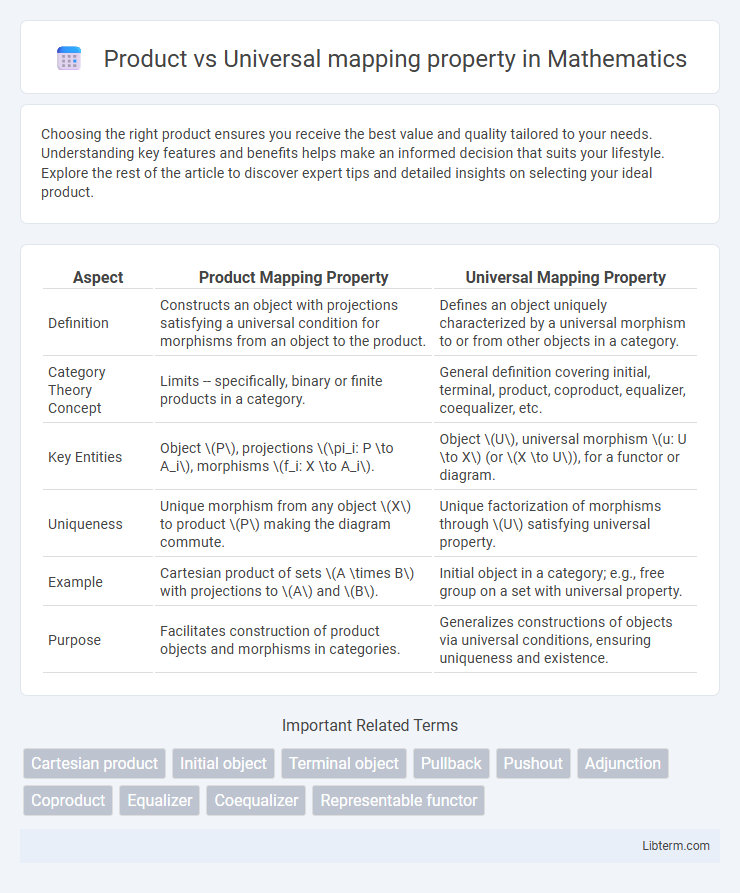
| Aspect | Product Mapping Property | Universal Mapping Property |
|---|---|---|
| Definition | Constructs an object with projections satisfying a universal condition for morphisms from an object to the product. | Defines an object uniquely characterized by a universal morphism to or from other objects in a category. |
| Category Theory Concept | Limits -- specifically, binary or finite products in a category. | General definition covering initial, terminal, product, coproduct, equalizer, coequalizer, etc. |
| Key Entities | Object \(P\), projections \(\pi_i: P \to A_i\), morphisms \(f_i: X \to A_i\). | Object \(U\), universal morphism \(u: U \to X\) (or \(X \to U\)), for a functor or diagram. |
| Uniqueness | Unique morphism from any object \(X\) to product \(P\) making the diagram commute. | Unique factorization of morphisms through \(U\) satisfying universal property. |
| Example | Cartesian product of sets \(A \times B\) with projections to \(A\) and \(B\). | Initial object in a category; e.g., free group on a set with universal property. |
| Purpose | Facilitates construction of product objects and morphisms in categories. | Generalizes constructions of objects via universal conditions, ensuring uniqueness and existence. |
Introduction to Product Mapping
Product mapping constructs a function from a single domain to a product of codomains by pairing individual component functions. This mapping leverages the universal property of the product to ensure a unique function exists matching all component projections. Such mappings are fundamental in category theory and set-based constructions, enabling the combination of multiple output spaces through a single coherent morphism.
Understanding the Universal Mapping Property
The Universal Mapping Property (UMP) characterizes objects in category theory by establishing a unique morphism from any object mapping into a given target through a specified construction, ensuring universality and uniqueness. This property generalizes the notion of product by defining objects via their universal characterization rather than explicit construction, allowing for abstraction across diverse categories. Understanding UMP involves recognizing that for any object mapping to components, there exists a unique morphism that factors through the universal object, highlighting its fundamental role in defining limits and colimits.
Defining Products in Category Theory
In category theory, the product of two objects \(A\) and \(B\) is defined by a universal mapping property involving a third object \(P\) and projection morphisms \(\pi_A: P \to A\) and \(\pi_B: P \to B\). For any object \(X\) with morphisms \(f: X \to A\) and \(g: X \to B\), there exists a unique morphism \(u: X \to P\) such that \(\pi_A \circ u = f\) and \(\pi_B \circ u = g\), characterizing \(P\) as the product \(A \times B\). This universal property distinguishes products by ensuring the factorization of morphisms uniquely through the product object, a hallmark feature differentiating it from general universal mapping properties.
Formal Statement of the Universal Mapping Property
The universal mapping property formally states that for a product object \(P\) with projection morphisms \(\pi_1: P \to A\) and \(\pi_2: P \to B\), any object \(X\) with morphisms \(f_1: X \to A\) and \(f_2: X \to B\) uniquely factors through \(P\) via a morphism \(u: X \to P\) such that \(\pi_1 \circ u = f_1\) and \(\pi_2 \circ u = f_2\). This property characterizes the product as a universal cone to the objects \(A\) and \(B\), ensuring uniqueness and existence of such factorization in any category. The formalism captures the essence of the product as a limiting construction defined purely by its mapping property, rather than by internal composition.
Examples of Product Objects
Product objects in category theory exemplify how pairs of objects combine to form a universal construction, where the product of sets A and B is the Cartesian product A x B with projection maps. In the category of topological spaces, the product object consists of the product space equipped with the product topology, alongside continuous projection functions. Similarly, for groups, the product object is the direct product of groups G and H, with group homomorphisms projecting onto each factor, fulfilling the universal property of the product.
Distinguishing Product and Universal Mapping Concepts
The Product property in category theory identifies an object that serves as a universal construction representing the pairing of two objects with projection morphisms, ensuring any other object's morphisms factor uniquely through it. The Universal Mapping Property (UMP) generalizes this idea, defining an object based on a universal morphism from or to a functor that all other such morphisms factor through uniquely. Distinguishing Product from UMP involves recognizing that the Product is a specific instance of universal mapping arising from the binary product functor, whereas UMP encompasses a broader class of universal constructions beyond products, such as coproducts, limits, and adjunctions.
Importance of the Universal Mapping Property
The Universal Mapping Property (UMP) provides a powerful and elegant way to characterize objects in category theory by ensuring unique factorization of morphisms, which simplifies the study of complex structures. Unlike product mapping properties that focus on projections, the UMP guarantees the existence and uniqueness of morphisms from any object into a target, making it essential for defining universal constructions such as limits, colimits, and adjoint functors. This uniqueness aspect enables mathematicians to identify canonical representatives and facilitates the enforcement of universal properties across diverse mathematical contexts.
Applications in Mathematics and Computer Science
Product and universal mapping properties are fundamental concepts in category theory with widespread applications in mathematics and computer science. In mathematics, product objects enable the construction of tuples and Cartesian products, facilitating the study of algebraic structures and topology through universal properties that guarantee uniqueness and existence of morphisms. In computer science, these properties underpin data type constructors, such as product types in programming languages, and model compositional semantics in functional programming and type theory, enabling modular design and reasoning about programs.
Limits, Products, and the Universal Property
The product in category theory exemplifies a limit defined by a universal property ensuring a unique morphism from any object to the product, preserving commutativity with projection morphisms. Universal properties characterize objects such as products by specifying how morphisms to or from these objects factor uniquely, enabling the construction of limits as universal cones. This semantic framework allows the categorical definition of products to serve as a prototype for all limits, highlighting their role in organizing data consistently across categories.
Summary: Key Differences and Insights
Product mapping property creates an object representing the Cartesian product with projection morphisms, uniquely factoring any pair of morphisms from a third object. Universal mapping property defines an object characterized by a unique morphism making a given diagram commute, often describing limits or colimits in category theory. The key difference lies in how products encapsulate multiple objects collectively, while universal properties emphasize unique factorization and characterization across morphisms.
Product Infographic
 libterm.com
libterm.com