Pontryagin classes are topological invariants associated with smooth manifolds, playing a crucial role in differential topology and geometry by characterizing the manifold's tangent bundle. These characteristic classes arise from the curvature form of a connection and provide essential tools for distinguishing manifolds that are homeomorphic but not diffeomorphic. Explore the rest of the article to deepen your understanding of Pontryagin classes and their applications in modern mathematics.
Table of Comparison
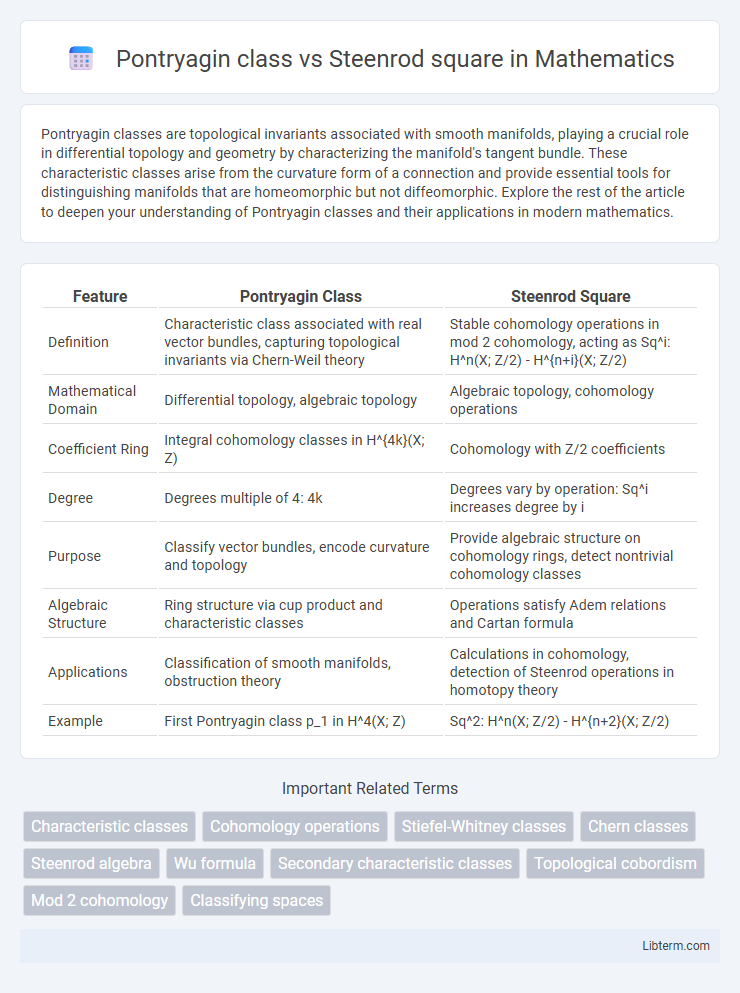
| Feature | Pontryagin Class | Steenrod Square |
|---|---|---|
| Definition | Characteristic class associated with real vector bundles, capturing topological invariants via Chern-Weil theory | Stable cohomology operations in mod 2 cohomology, acting as Sq^i: H^n(X; Z/2) - H^{n+i}(X; Z/2) |
| Mathematical Domain | Differential topology, algebraic topology | Algebraic topology, cohomology operations |
| Coefficient Ring | Integral cohomology classes in H^{4k}(X; Z) | Cohomology with Z/2 coefficients |
| Degree | Degrees multiple of 4: 4k | Degrees vary by operation: Sq^i increases degree by i |
| Purpose | Classify vector bundles, encode curvature and topology | Provide algebraic structure on cohomology rings, detect nontrivial cohomology classes |
| Algebraic Structure | Ring structure via cup product and characteristic classes | Operations satisfy Adem relations and Cartan formula |
| Applications | Classification of smooth manifolds, obstruction theory | Calculations in cohomology, detection of Steenrod operations in homotopy theory |
| Example | First Pontryagin class p_1 in H^4(X; Z) | Sq^2: H^n(X; Z/2) - H^{n+2}(X; Z/2) |
Introduction to Pontryagin Classes and Steenrod Squares
Pontryagin classes are topological invariants associated with real vector bundles, capturing essential information about their curvature and underlying manifold structure in differential topology. Steenrod squares are cohomology operations that act on cohomology classes mod 2, playing a fundamental role in algebraic topology by providing stable operations in the cohomology ring. Understanding Pontryagin classes and Steenrod squares enables deep insights into characteristic classes, their algebraic properties, and their applications in classifying manifolds and vector bundles.
Historical Development and Mathematical Context
Pontryagin classes, introduced by Lev Pontryagin in the 1940s, are characteristic classes used to study smooth manifolds and their tangent bundles through cohomology with integral coefficients. Steenrod squares, developed by Norman Steenrod in the late 1940s, form a family of cohomology operations acting on mod 2 cohomology, playing a crucial role in algebraic topology and the study of fiber bundles. The interplay between Pontryagin classes and Steenrod squares has enriched the understanding of manifold invariants, linking differential topology and algebraic topology in the classification of vector bundles.
Definitions: Pontryagin Class Explained
Pontryagin classes are topological invariants associated with real vector bundles, defined using the curvature form of a connection and representing elements in the integral cohomology ring with degrees divisible by four. Steenrod squares are operations in mod 2 cohomology that act as cohomology ring homomorphisms and provide algebraic structures capturing the failure of graded commutativity. While Pontryagin classes characterize smooth manifold tangential structures via characteristic classes, Steenrod squares encode finer cohomological relations and detect obstructions in mod 2 cohomology.
Definitions: Steenrod Square Demystified
Steenrod squares are stable cohomology operations defined in mod 2 cohomology, acting on the cohomology groups \( H^n(X; \mathbb{Z}/2\mathbb{Z}) \) of a topological space \( X \) to produce elements in \( H^{n+k}(X; \mathbb{Z}/2\mathbb{Z}) \), encapsulating information about the cup product structure. Pontryagin classes, by contrast, are characteristic classes associated with real vector bundles, lying in integral cohomology groups \( H^{4k}(X; \mathbb{Z}) \), and capture topological invariants related to the bundle's curvature and smooth structure. The Steenrod square \( Sq^k \) can be viewed as a mod 2 operation that indirectly influences Pontryagin classes through relations and reductions mod 2, linking these fundamental concepts within algebraic topology.
Algebraic Topology: The Core Theoretical Framework
Pontryagin classes are characteristic classes associated with real vector bundles, capturing geometric information through cohomology classes in even degrees, specifically in integral cohomology. Steenrod squares are cohomology operations defined on mod 2 cohomology, generating secondary structure by acting on the cohomology ring and providing obstructions to certain bundle trivializations. In algebraic topology, understanding the interaction between Pontryagin classes and Steenrod squares elucidates the linkage between characteristic classes and cohomology operations, enhancing the classification of manifold invariants and vector bundle structures.
Distinctions in Construction and Application
Pontryagin classes arise from characteristic classes associated with real vector bundles and are defined using curvature forms or Chern-Weil theory, while Steenrod squares are cohomology operations defined in mod 2 cohomology that act on the cohomology ring of topological spaces. Pontryagin classes capture geometric information related to smooth manifold structures and tangential bundle properties, whereas Steenrod squares encode algebraic invariants reflecting the failure of the cup product to be strictly commutative. The application of Pontryagin classes is central in differential topology and surgery theory for classifying manifolds, while Steenrod squares play a key role in homotopy theory, obstruction theory, and computations in stable cohomology.
Relationships and Interactions Between the Two Invariants
Pontryagin classes and Steenrod squares interact through the action of Steenrod operations on the characteristic classes of real vector bundles, where Steenrod squares provide cohomological operations that detect mod 2 reductions of Pontryagin classes. The mod 2 reduction of Pontryagin classes can be expressed in terms of Steenrod squares acting on Stiefel-Whitney classes, highlighting a deep connection between these invariants in the study of smooth manifold topology. This relationship plays a crucial role in obstruction theory and the classification of fiber bundles, linking integral characteristic classes with mod 2 cohomology operations.
Examples Illustrating Computation and Use
Pontryagin classes are characteristic classes associated with real vector bundles that are computed via curvature forms and play a critical role in classifying smooth manifolds, such as the first Pontryagin class of the tangent bundle of the 4-sphere S^4 being zero. Steenrod squares, mod 2 cohomology operations, provide secondary invariants that detect nontriviality in cup product structures, notably in the cohomology of projective spaces like RP^n where the action of Sq^1 and Sq^2 determines the structure of H^*(RP^n; Z/2). Concrete computations include using Steenrod squares to compute the Stiefel-Whitney classes, which in turn relate to Pontryagin classes via the Whitney sum formula and Wu formulas, enabling topologists to discern subtle manifold properties like orientability and spin structures.
Impacts on Modern Topology and Geometry
Pontryagin classes provide crucial invariants in the classification of smooth manifolds, influencing the study of vector bundles and characteristic classes in differential topology. Steenrod squares, as cohomology operations, enhance the algebraic structure of cohomology rings, enabling finer distinctions between topological spaces and contributing to the development of stable homotopy theory. The interplay between Pontryagin classes and Steenrod squares deepens understanding of manifold invariants and has driven advances in cobordism theory and characteristic class computations within modern geometric topology.
Open Problems and Future Research Directions
Open problems in the study of Pontryagin classes and Steenrod squares include understanding their interactions in higher-dimensional manifolds and refining computational methods for characteristic classes in complex topologies. Future research is directed towards developing generalized cohomology theories that integrate Steenrod operations with Pontryagin classes, enhancing the classification of smooth structures. Investigations into equivariant versions and applications in string theory and quantum field theory highlight emerging interdisciplinary directions.
Pontryagin class Infographic
 libterm.com
libterm.com