An inner product space is a vector space equipped with an inner product, a function that allows the measurement of angles and lengths by mapping pairs of vectors to scalars. This structure generalizes the dot product in Euclidean space and is fundamental for defining orthogonality, projections, and norms. Explore the article to deepen your understanding of inner product spaces and their applications in mathematics and physics.
Table of Comparison
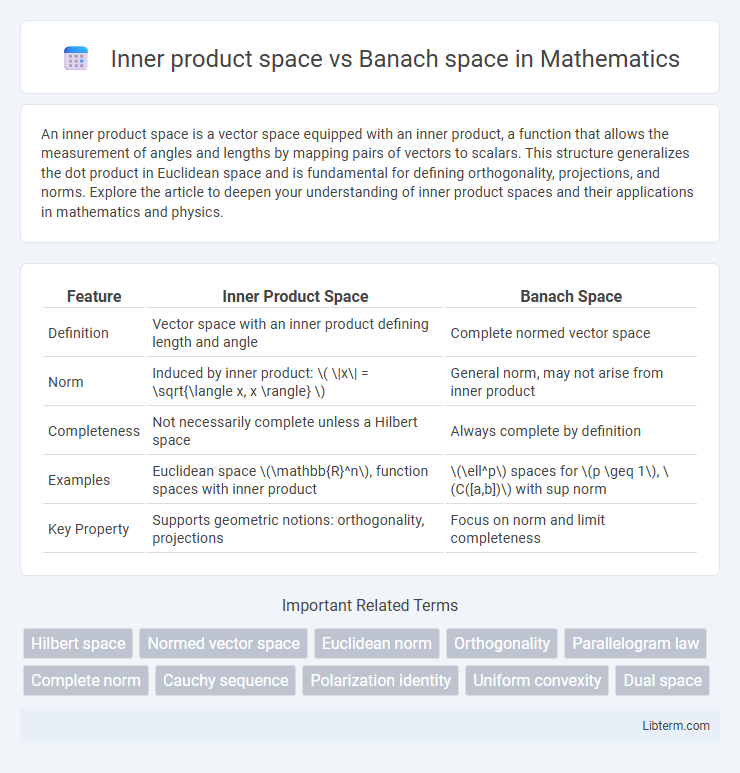
| Feature | Inner Product Space | Banach Space |
|---|---|---|
| Definition | Vector space with an inner product defining length and angle | Complete normed vector space |
| Norm | Induced by inner product: \( \|x\| = \sqrt{\langle x, x \rangle} \) | General norm, may not arise from inner product |
| Completeness | Not necessarily complete unless a Hilbert space | Always complete by definition |
| Examples | Euclidean space \(\mathbb{R}^n\), function spaces with inner product | \(\ell^p\) spaces for \(p \geq 1\), \(C([a,b])\) with sup norm |
| Key Property | Supports geometric notions: orthogonality, projections | Focus on norm and limit completeness |
Introduction to Inner Product Spaces and Banach Spaces
Inner product spaces are vector spaces equipped with an inner product, enabling the measurement of angles and lengths, thereby generalizing Euclidean geometry to abstract spaces. Banach spaces are complete normed vector spaces with a norm that induces a metric, ensuring convergence of Cauchy sequences within the space. While all inner product spaces induce a norm and can be complete, forming Hilbert spaces, Banach spaces need not arise from an inner product, highlighting the distinction between geometric structures and purely normed completeness.
Fundamental Definitions and Concepts
Inner product spaces are vector spaces equipped with an inner product, a positive-definite sesquilinear form that induces a norm and defines geometric concepts such as angles and orthogonality. Banach spaces are complete normed vector spaces where the norm need not arise from an inner product, emphasizing completeness with respect to metric convergence. The fundamental distinction lies in the inner product's ability to generate the norm in inner product spaces, while Banach spaces require only completeness under any norm, enabling broader applications in functional analysis.
Structure of Inner Product Spaces
Inner product spaces feature a structure defined by an inner product, a positive-definite, symmetric bilinear form enabling notions of angle, length, and orthogonality, which are fundamental for geometric interpretations and projections. This inner product induces a norm, turning the space into a normed vector space, but not all normed spaces arise from an inner product. Banach spaces are complete normed vector spaces, and while every inner product space with a complete norm is a Hilbert space (a special kind of Banach space), Banach spaces do not necessarily have an inner product structure, emphasizing that inner product spaces possess richer geometric and algebraic features.
Key Properties of Banach Spaces
Banach spaces are complete normed vector spaces where every Cauchy sequence converges within the space, a crucial property for ensuring the stability of limits and functional analysis applications. Unlike inner product spaces, Banach spaces need not have an inner product structure but possess a norm satisfying the triangle inequality and homogeneity. The completeness and norm structure of Banach spaces facilitate powerful theorems such as the Hahn-Banach theorem, the Banach-Steinhaus theorem, and the Open Mapping theorem, fundamental tools in analysis and partial differential equations.
Norms: Comparisons and Contrasts
Inner product spaces feature norms derived from the inner product, satisfying the parallelogram law, which guarantees a geometric structure enabling angles and orthogonality analyses. Banach spaces rely on a complete norm not necessarily induced by an inner product, allowing a broader class of normed spaces without geometric constraints. The key distinction lies in norm origin and associated properties: inner product norms arise from a bilinear form, while Banach space norms merely require completeness under the metric induced by the norm.
Geometric Interpretations
Inner product spaces provide a geometric structure where angles and lengths are well-defined through the inner product, allowing concepts like orthogonality and projections to be visualized clearly. Banach spaces, endowed with a norm that may not arise from an inner product, lack a natural notion of angle, making geometric interpretations more abstract and focused on distance and convergence. The parallelogram law characterizes those Banach spaces that are inner product spaces, highlighting the intrinsic geometric differences between the two.
Examples in Functional Analysis
Inner product spaces, such as Hilbert spaces including \( L^2(\mathbb{R}) \), are equipped with an inner product that induces a norm, enabling the use of geometric notions like orthogonality and projections. Banach spaces, exemplified by \( L^p(\mathbb{R}) \) for \( 1 \leq p < \infty \) with \( p \neq 2 \), are complete normed vector spaces that need not have an inner product structure, making them more general but lacking the full geometric framework. In functional analysis, the distinction is critical as Hilbert spaces are central to quantum mechanics and signal processing due to their rich geometry, while Banach spaces cover broader classes of function spaces essential for studying differential equations and operator theory.
Applications in Mathematics and Physics
Inner product spaces provide the foundational framework for quantum mechanics and signal processing through their geometric structure, enabling notions of angles and orthogonality essential for wavefunction analysis and Fourier transforms. Banach spaces, characterized by norm completeness without requiring an inner product, are crucial in the study of differential equations, fixed point theory, and optimization problems in functional analysis. Applications in physics often rely on Hilbert spaces, a subclass of Banach spaces with inner products, while Banach spaces facilitate the treatment of more general spaces arising in nonlinear analysis and PDEs.
Advantages and Limitations of Each Space
Inner product spaces offer geometric structure through the inner product, enabling concepts like orthogonality and projection, which facilitate methods such as Fourier analysis and optimization algorithms; however, they require the space to be complete with respect to the norm induced by the inner product to ensure convergence and stability. Banach spaces, being complete normed vector spaces, provide a broader framework that supports various functional analysis techniques and fixed point theorems, but lack the inner product structure, limiting geometric interpretations and certain decomposition techniques. The choice between inner product and Banach spaces depends on the necessity of geometric tools versus the generality of completeness under arbitrary norms.
Summary and Choosing the Right Space
Inner product spaces are complete normed vector spaces where the norm is induced by an inner product, allowing geometric concepts such as angles and orthogonality. Banach spaces are complete normed vector spaces that may lack an inner product, providing a more general framework suitable for broader functional analysis applications. Choosing between an inner product space and a Banach space depends on whether the problem requires geometric structure and inner product properties or simply completeness with respect to a norm.
Inner product space Infographic
 libterm.com
libterm.com