Tensor is a mathematical object used extensively in physics and engineering to represent multi-dimensional data and relationships between geometric quantities. Its core function is to generalize scalars, vectors, and matrices to higher dimensions, enabling complex transformations in fields like machine learning and computer vision. Discover how understanding tensors can empower your grasp of advanced technologies throughout the rest of this article.
Table of Comparison
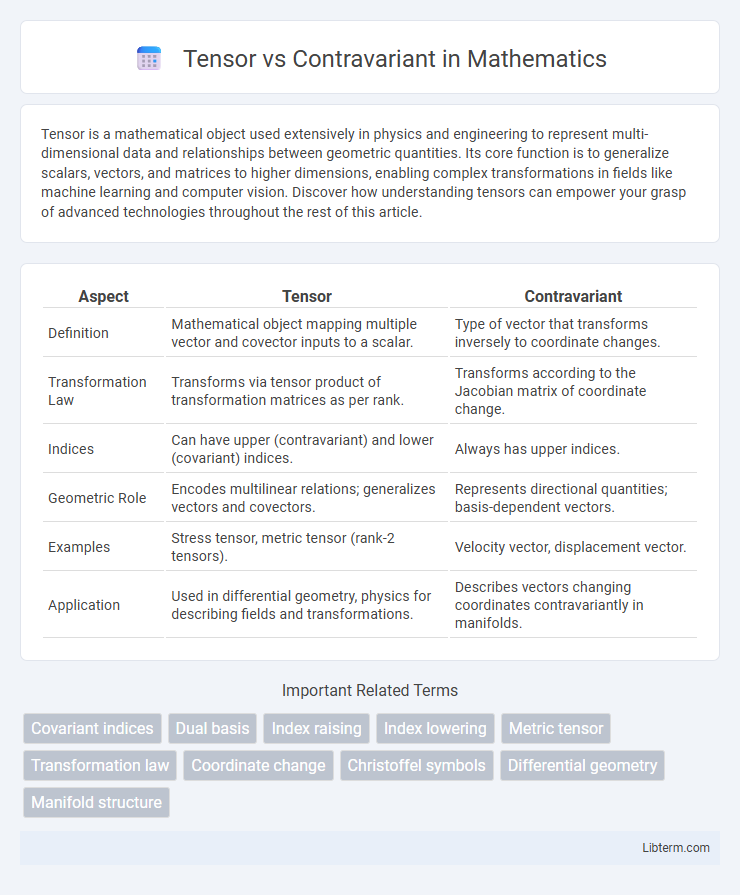
| Aspect | Tensor | Contravariant |
|---|---|---|
| Definition | Mathematical object mapping multiple vector and covector inputs to a scalar. | Type of vector that transforms inversely to coordinate changes. |
| Transformation Law | Transforms via tensor product of transformation matrices as per rank. | Transforms according to the Jacobian matrix of coordinate change. |
| Indices | Can have upper (contravariant) and lower (covariant) indices. | Always has upper indices. |
| Geometric Role | Encodes multilinear relations; generalizes vectors and covectors. | Represents directional quantities; basis-dependent vectors. |
| Examples | Stress tensor, metric tensor (rank-2 tensors). | Velocity vector, displacement vector. |
| Application | Used in differential geometry, physics for describing fields and transformations. | Describes vectors changing coordinates contravariantly in manifolds. |
Understanding Tensors: The Basics
Tensors generalize scalars, vectors, and matrices by representing multilinear relationships between geometric vectors, scalars, and other tensors. Contravariant tensors specifically transform oppositely to the coordinate basis under a change of basis, embodying directional components such as displacement vectors. Understanding these transformation properties is crucial for distinguishing between tensor types and accurately applying them in physics and engineering contexts.
Covariant vs. Contravariant: Core Definitions
Covariant and contravariant refer to how tensor components transform under a change of basis: covariant components transform with the basis, while contravariant components transform inversely. A covariant vector (or covector) has components that lower indices and transform using the basis change matrix, representing gradients or dual vectors. Contravariant vectors have raised indices and transform using the inverse matrix, representing directions or displacements in a vector space.
Geometric Interpretation of Vectors and Dual Vectors
In differential geometry, tensors are multilinear maps that generalize vectors and covectors, where vectors represent directional derivatives at a point on a manifold, embodying movement or flow. Contravariant vectors transform according to the inverse of the coordinate change, reflecting directional quantities, while covariant vectors, or dual vectors, transform directly with the coordinate change, measuring rates of change of scalar fields. The geometric interpretation distinguishes contravariant vectors as arrows in the tangent space and covariant vectors as linear functionals in the cotangent space, establishing a duality fundamental to tensor calculus and manifold analysis.
Index Notation in Tensor Analysis
Index notation in tensor analysis distinguishes tensors by the position of their indices: covariant indices are written as subscripts, representing components that transform with the basis, while contravariant indices appear as superscripts, denoting components that transform inversely to the basis. A tensor with mixed variance includes both types, such as \( T^i_j \), where the upper index \( i \) is contravariant and the lower index \( j \) is covariant, encoding how the tensor transforms under coordinate changes. Understanding the roles of covariant and contravariant indices is essential in operations such as tensor contraction, which sums over one contravariant and one covariant index to produce an invariant scalar or lower-rank tensor.
Transformation Properties: Covariant and Contravariant Components
Tensor transformation properties distinguish between covariant and contravariant components by how they change under coordinate transformations: contravariant components transform with the Jacobian matrix of the coordinate change, reflecting vector behavior that follows the transformation of basis vectors. Covariant components transform with the inverse Jacobian matrix, aligning with dual vectors or covectors that act against the transformation direction. This distinction is fundamental in tensor calculus, ensuring that tensors maintain consistent geometric and physical interpretations independently of the chosen coordinate system.
Metric Tensor and Index Raising/Lowering
The metric tensor serves as the fundamental tool for index raising and lowering, transforming contravariant vectors into covariant vectors and vice versa by contracting indices with its components. Contravariant components, associated with basis vectors, are transformed into covariant components through the metric tensor \( g_{\mu\nu} \), which encodes the geometric and distance properties of the manifold. This tensorial operation is essential in differential geometry and general relativity, allowing seamless transition between different tensor types while preserving the manifold's intrinsic geometry.
Contravariant and Covariant Tensors in Physics
Contravariant tensors transform with the inverse of the coordinate transformation matrix and are associated with vector components that change like displacement or velocity, while covariant tensors transform directly with the coordinate matrix and relate to gradients or dual vectors. In physics, contravariant tensors often represent physical quantities such as velocity or momentum, whereas covariant tensors correspond to quantities like force or electric field intensity that interact with those vectors. Understanding the distinction between covariant and contravariant tensors is essential for formulating laws of physics in curved spacetime and ensures coordinate-independent descriptions in general relativity and field theory.
Coordinate Systems and Basis Transformations
Tensors are geometric objects independent of coordinate systems, characterized by their transformation rules under a change of basis, which involve both covariant and contravariant components. Contravariant vectors transform according to the inverse Jacobian matrix of the coordinate transformation, reflecting changes in vector components relative to basis vectors, while covariant vectors transform with the Jacobian matrix itself, corresponding to dual basis transformations. This distinction in transformation behavior under coordinate changes ensures tensors maintain intrinsic geometric meaning across different reference frames.
Practical Examples: General Relativity Applications
In general relativity, tensors describe physical quantities such as the stress-energy tensor, which embodies energy density and momentum flux in spacetime. Contravariant vectors, like displacement vectors, transform oppositely to the coordinate basis under changes in the reference frame and represent directions or velocities. These distinctions are crucial when formulating Einstein's field equations, ensuring the geometric properties of spacetime remain consistent across different coordinate systems.
Summary: Distinguishing Tensors and Contravariant Objects
Tensors are multilinear maps that combine covariant and contravariant components, representing geometric and physical quantities invariant under coordinate transformations. Contravariant objects are components of vectors that transform inversely to the basis vectors, distinguished by their upper indices in tensor notation. Understanding the difference hinges on recognizing tensors as generalized entities encompassing both contravariant and covariant elements, while contravariant components specifically refer to vector parts transforming with the inverse Jacobian matrix.
Tensor Infographic
 libterm.com
libterm.com