Hausdorff measure generalizes the concept of length, area, and volume for irregular and fractal sets by considering coverings with arbitrarily small diameters and scaling parameters. It is essential in fractal geometry and geometric measure theory, providing a rigorous way to analyze dimensions of complex shapes beyond integer dimensions. Explore the rest of the article to understand how Hausdorff measure applies to your study of geometric structures.
Table of Comparison
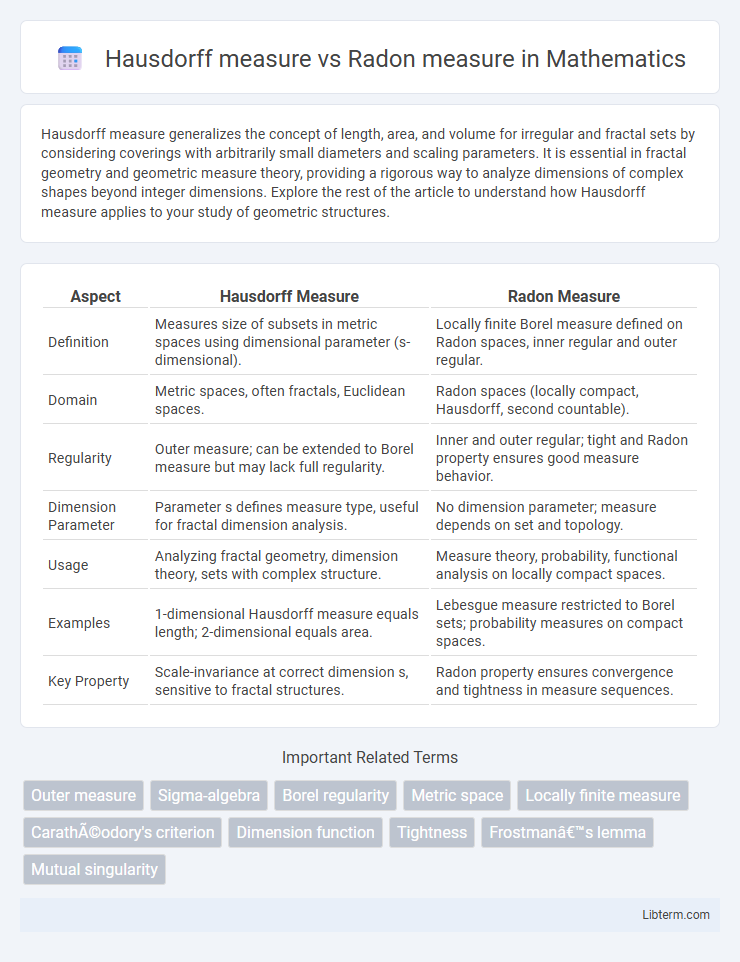
| Aspect | Hausdorff Measure | Radon Measure |
|---|---|---|
| Definition | Measures size of subsets in metric spaces using dimensional parameter (s-dimensional). | Locally finite Borel measure defined on Radon spaces, inner regular and outer regular. |
| Domain | Metric spaces, often fractals, Euclidean spaces. | Radon spaces (locally compact, Hausdorff, second countable). |
| Regularity | Outer measure; can be extended to Borel measure but may lack full regularity. | Inner and outer regular; tight and Radon property ensures good measure behavior. |
| Dimension Parameter | Parameter s defines measure type, useful for fractal dimension analysis. | No dimension parameter; measure depends on set and topology. |
| Usage | Analyzing fractal geometry, dimension theory, sets with complex structure. | Measure theory, probability, functional analysis on locally compact spaces. |
| Examples | 1-dimensional Hausdorff measure equals length; 2-dimensional equals area. | Lebesgue measure restricted to Borel sets; probability measures on compact spaces. |
| Key Property | Scale-invariance at correct dimension s, sensitive to fractal structures. | Radon property ensures convergence and tightness in measure sequences. |
Introduction to Measures in Mathematics
Hausdorff measure generalizes the concept of length, area, and volume to non-integer dimensions and fractal sets, playing a crucial role in geometric measure theory. Radon measure extends the Lebesgue measure framework, allowing integration over locally compact Hausdorff spaces and providing a foundation for functional analysis and probability theory. Both measures serve as fundamental tools in analyzing the size and structure of subsets within metric and topological spaces.
Defining Hausdorff Measure
Hausdorff measure generalizes the concept of Lebesgue measure by assigning a measure to subsets of a metric space using a scale parameter called dimension, defined through coverings with sets of small diameter and a dimension-dependent scaling factor. It is constructed as the limit of outer measures based on the infimum of sums of diameters raised to the power of the chosen dimension, capturing fractal and irregular structures effectively. In contrast, Radon measures are regular Borel measures finite on compact sets, primarily characterized by their topological and measure-theoretic properties without explicit dimensional parameters.
Defining Radon Measure
Radon measures are defined as locally finite Borel measures that are inner regular, meaning the measure of any Borel set can be approximated from within by compact subsets. In contrast, Hausdorff measures generalize the concept of length, area, and volume by measuring subsets in metric spaces using dimensional parameters. Radon measures provide a flexible framework for integration on locally compact spaces, supporting key properties like tightness and regularity which are essential in analysis and probability theory.
Historical Background and Development
Hausdorff measure, developed by Felix Hausdorff in 1919, extended classical notions of measure to fractal and irregular sets by introducing dimension-based scaling, crucial for geometric measure theory. The Radon measure, rooted in Johann Radon's 1913 work on integral representation, generalized measures on locally compact spaces, establishing a foundation for modern functional analysis and measure theory. Both measures evolved through the 20th century, influencing fields like probability, analysis, and topology by providing frameworks to quantify size and distribution beyond Euclidean structures.
Key Properties of Hausdorff Measure
Hausdorff measure is a fundamental tool in geometric measure theory used to analyze the size and dimension of fractal and irregular sets, defined for any non-negative real dimension and generalizing the notion of length, area, and volume. It is characterized by its outer regularity, countable subadditivity, and zero measure for countable sets, making it suitable for measuring sets with complex geometric structures. Unlike Radon measures, Hausdorff measure explicitly depends on a dimension parameter and is tightly connected to Hausdorff dimension, allowing precise quantification of fractal geometry.
Key Properties of Radon Measure
Radon measures are locally finite and inner regular Borel measures defined on Hausdorff topological spaces, supporting strong integration and approximation properties unmatched by general Hausdorff measures. Unlike Hausdorff measures, which primarily quantify size and dimension of fractal sets, Radon measures enable tight integration theory applications due to their tightness and outer regularity on Borel sets. The key properties include local finiteness, inner regularity (approximation by compact sets), and outer regularity (approximation from open sets), making Radon measures central in analysis, probability, and geometric measure theory.
Comparison: Hausdorff vs. Radon Measures
Hausdorff measures generalize the notion of length, area, and volume to non-integer dimensions by assigning measures to fractals and irregular sets, while Radon measures encompass locally finite, Borel measures that are both inner regular and outer regular on topological spaces. Hausdorff measures are often utilized in geometric measure theory to analyze fractal dimensions and metric properties, whereas Radon measures provide a more general framework suitable for integration and probability theory in locally compact spaces. The choice between them depends on the underlying space and the desired properties, with Hausdorff measures excelling in dimension-sensitive analysis and Radon measures in topological and functional analytic contexts.
Applications in Geometry and Analysis
Hausdorff measure plays a critical role in fractal geometry by quantifying the size of irregular sets, enabling precise dimension theory analysis. Radon measure serves as a fundamental tool in functional analysis and PDEs, providing a versatile framework for integrating over locally compact spaces. Both measures facilitate the study of geometric properties and regularity of sets and functions, with Hausdorff measure focusing on fine-scale geometric detail and Radon measure supporting broader integration and distribution theories.
Limitations and Special Cases
Hausdorff measure, often used to analyze fractal dimensions, faces limitations in handling measures on sets with irregular or highly fragmented structures, where it may assign zero or infinite measure unintuitively. Radon measure, being a locally finite Borel measure, excels in representing measures on locally compact spaces, yet struggles with non-locally compact spaces where its regularity conditions fail. Special cases arise when Hausdorff measures coincide with Lebesgue measures on Euclidean spaces, while Radon measures generalize these concepts to support broader functional analysis frameworks.
Conclusion and Future Directions
Hausdorff measure provides a flexible framework for analyzing fractal and irregular geometric sets by generalizing dimensional concepts, while Radon measure offers robust tools for integration and functional analysis on locally compact spaces. Future research may enhance the interplay between these measures, exploring extensions to non-Euclidean geometries and developing computational methods for high-dimensional fractal analysis. Advances in this area could lead to refined applications in geometric measure theory, probability, and mathematical physics.
Hausdorff measure Infographic
 libterm.com
libterm.com