A well-crafted section in any text enhances clarity and ensures key points are effectively communicated. Focusing on concise, relevant information helps maintain reader engagement and improves overall understanding. Discover how structuring your sections can transform your writing by reading the rest of the article.
Table of Comparison
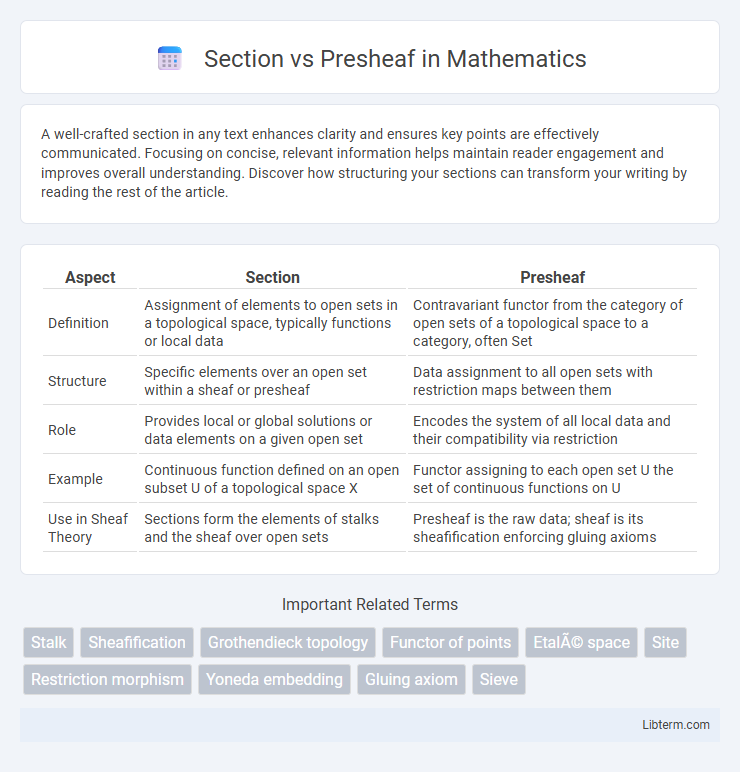
| Aspect | Section | Presheaf |
|---|---|---|
| Definition | Assignment of elements to open sets in a topological space, typically functions or local data | Contravariant functor from the category of open sets of a topological space to a category, often Set |
| Structure | Specific elements over an open set within a sheaf or presheaf | Data assignment to all open sets with restriction maps between them |
| Role | Provides local or global solutions or data elements on a given open set | Encodes the system of all local data and their compatibility via restriction |
| Example | Continuous function defined on an open subset U of a topological space X | Functor assigning to each open set U the set of continuous functions on U |
| Use in Sheaf Theory | Sections form the elements of stalks and the sheaf over open sets | Presheaf is the raw data; sheaf is its sheafification enforcing gluing axioms |
Introduction: Section vs Presheaf
Sections represent individual, continuous selections of elements within a bundle or sheaf over a topological space, providing localized data that vary smoothly with respect to the base space. Presheaves assign algebraic or set-theoretic structures to open sets along with restriction maps, thereby encoding how local data can be consistently compared across overlapping regions. The distinction centers on sections as particular elements in the total space, while presheaves formalize the systematic organization of such local data across all open subsets.
Foundational Concepts: What are Sections?
Sections are fundamental objects in sheaf theory representing consistent selections of data over open subsets of a topological space, functioning as elements of presheaves or sheaves. A section assigns to every open set in the space a corresponding element in a structured set or category, ensuring compatibility with restriction maps when domains shrink. This concept underpins the ability to study local-global principles by relating local data coherently to global structures in geometric and algebraic contexts.
Understanding Presheaves: Formal Definition
A presheaf on a topological space assigns to each open set a set (or algebraic structure) and to each inclusion of open sets a restriction map, satisfying identity and composition conditions. Sections refer to elements of the assigned sets over specific open sets, providing local data that the presheaf organizes systematically. Understanding presheaves involves appreciating how these local sections and restriction maps encode varying local information across the topology.
Comparing Sections and Presheaves: Key Differences
Sections represent specific elements or choices within a presheaf's structure, providing local data over open subsets of a topological space, while presheaves systematically associate data to each open set along with restriction maps. Key differences include that sections are individual instances extracted from the broader framework of a presheaf's assignments, whereas presheaves encompass the entire collection of data and morphisms that define local-global relationships. This distinction highlights how presheaves serve as functorial tools encoding spatial data, while sections act as concrete values or solutions within that context.
The Role of Sections in Sheaf Theory
Sections serve as fundamental building blocks in sheaf theory, representing local data assignments over open subsets of a topological space that adhere to consistency conditions on overlaps. These local sections enable the construction of a presheaf, which collects these assignments but may lack the gluing and locality axioms required for a sheaf. The role of sections is crucial in transitioning from a presheaf to a sheaf by ensuring that compatible local sections uniquely determine a global section, capturing the essence of locality and globality in sheaf theory.
Applications of Presheaves in Topology
Presheaves assign algebraic structures to open sets in a topological space, enabling local-to-global analysis crucial in topology. Unlike sections that provide local elements of a sheaf, presheaves capture broader information by encoding data functorially over the entire open set lattice. Applications of presheaves include constructing cohomology theories, defining etale spaces, and facilitating descent theory, which are fundamental in studying continuous functions and fiber bundles.
Functorial Nature: Sections vs Presheaves
Sections are concrete instances of local data assignments over open sets in a topological space, whereas presheaves represent a functorial framework assigning data contravariantly to all open sets and restriction maps. The presheaf encodes the algebraic structure and compatibility conditions across open sets via its contravariant functor from the category of open sets to a target category, typically sets or groups. Sections correspond to specific elements within presheaves, reflecting local realizations of the abstract data encoded by the functor.
Examples Illustrating Sections and Presheaves
Sections represent individual continuous choices or selections of elements from each fiber in a fiber bundle, such as choosing a consistent tangent vector at every point on a manifold, forming a smooth vector field. In contrast, presheaves assign data structures, like sets or rings, to open subsets of a topological space, exemplified by the presheaf of continuous real-valued functions where each open set corresponds to its ring of functions. Examples include the section of a sheaf of differentiable functions yielding smooth functions on an open domain, while the associated presheaf encapsulates restrictions of these functions to smaller open subsets, illustrating the local-to-global property.
Importance in Category Theory and Algebraic Geometry
Sections and presheaves are foundational concepts in category theory and algebraic geometry, with presheaves serving as functors that assign algebraic structures to open sets in a topological space, encoding local data. Sections represent elements of these structures over specific open sets, enabling the study of local-global principles that are crucial for understanding sheafification and cohomology. The interplay between sections and presheaves facilitates the construction of sheaves, which are essential for formulating geometric objects and solving problems involving localization and gluing in algebraic geometry.
Conclusion: Choosing Between Sections and Presheaves
Choosing between sections and presheaves depends on the specific needs of your mathematical framework; sections provide concrete elements tied to open sets, enhancing local analysis, while presheaves offer a broader, more flexible structure capturing variable data across spaces. Presheaves are essential for constructing sheaves, enabling powerful tools in topology and algebraic geometry, whereas sections serve as practical tools for explicit computations and local-global interactions. The decision hinges on balancing the abstraction level required and the nature of the problem, with presheaves excelling in theoretical constructions and sections offering tangible local insights.
Section Infographic
 libterm.com
libterm.com