Interior Point methods optimize complex problems efficiently by navigating the feasible region's interior rather than its boundaries. These algorithms are essential in large-scale linear and nonlinear programming, offering greater speed and stability compared to traditional simplex approaches. Explore the article to understand how Interior Point techniques can enhance Your optimization tasks.
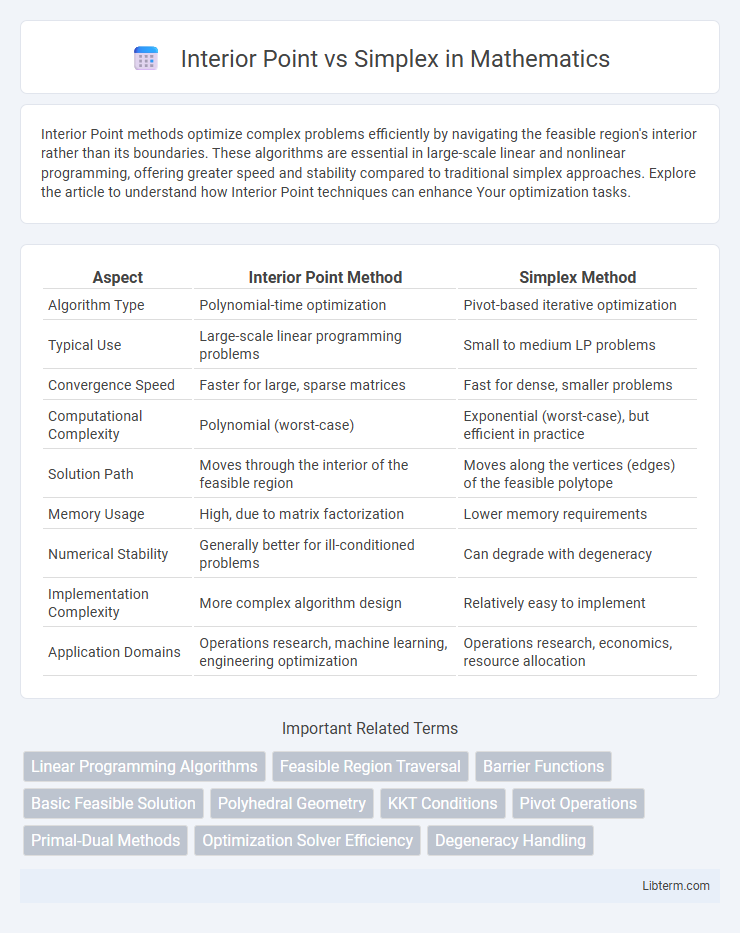
Table of Comparison
| Aspect | Interior Point Method | Simplex Method |
|---|---|---|
| Algorithm Type | Polynomial-time optimization | Pivot-based iterative optimization |
| Typical Use | Large-scale linear programming problems | Small to medium LP problems |
| Convergence Speed | Faster for large, sparse matrices | Fast for dense, smaller problems |
| Computational Complexity | Polynomial (worst-case) | Exponential (worst-case), but efficient in practice |
| Solution Path | Moves through the interior of the feasible region | Moves along the vertices (edges) of the feasible polytope |
| Memory Usage | High, due to matrix factorization | Lower memory requirements |
| Numerical Stability | Generally better for ill-conditioned problems | Can degrade with degeneracy |
| Implementation Complexity | More complex algorithm design | Relatively easy to implement |
| Application Domains | Operations research, machine learning, engineering optimization | Operations research, economics, resource allocation |
Introduction to Linear Programming Optimization
Interior Point methods and the Simplex algorithm are two primary techniques for solving Linear Programming (LP) optimization problems. The Simplex method traverses the vertices of the feasible region polytope, seeking the optimal corner point, while Interior Point algorithms progress through the interior of the feasible region, efficiently handling large-scale LPs. Both methods optimize linear objective functions subject to linear equality and inequality constraints, but Interior Point methods often provide faster convergence for high-dimensional or sparse problems common in modern optimization scenarios.
Overview of the Simplex Method
The Simplex Method is a widely used algorithm for solving linear programming problems by iteratively moving along the edges of the feasible region defined by constraints to find the optimal vertex. It operates in polynomial time in practice, despite having exponential worst-case complexity, making it efficient for many real-world applications. The method systematically improves the objective function value by pivoting between adjacent basic feasible solutions until no further improvement is possible.
Fundamentals of the Interior Point Method
The Interior Point Method solves linear optimization problems by traversing the feasible region's interior, following a path toward the optimal solution using barrier functions that prevent crossing boundaries. It employs primal-dual algorithms to simultaneously update both primal and dual variables, achieving polynomial-time convergence compared to the Simplex method's exponential worst-case complexity. Key components include logarithmic barrier functions, Newton's method for solving nonlinear equations, and central path concepts that guide iterations efficiently within high-dimensional constraint spaces.
Key Differences Between Simplex and Interior Point
The Simplex algorithm traverses the vertices of the feasible region in a linear programming problem, optimizing at corner points, while Interior Point methods move through the interior of the feasible region, following a path toward the optimal solution. Simplex is typically effective for smaller to medium-sized problems with good precision on vertex solutions, whereas Interior Point algorithms handle large-scale, sparse problems more efficiently and provide polynomial-time performance. Key differences include Simplex's vertex-focused iteration versus Interior Point's trajectory through the feasible region's interior, and their distinct computational complexities and scalability in practical optimization scenarios.
Computational Efficiency and Scalability
Interior Point methods demonstrate superior computational efficiency in solving large-scale linear programming problems by utilizing polynomial-time algorithms and matrix factorization techniques, making them highly scalable for complex datasets. In contrast, the Simplex method, while efficient for small to medium-sized problems, experiences exponential worst-case time complexity, limiting its scalability and performance as problem size increases. Empirical studies consistently show Interior Point algorithms outperform Simplex in terms of iteration count and total runtime when addressing high-dimensional optimization tasks.
Solution Accuracy and Precision
Interior Point methods generally provide high solution accuracy by efficiently navigating the feasible region's interior, achieving precise optimal points in large-scale linear programming problems. Simplex algorithms deliver exact vertex solutions with strong precision but may struggle with numerical instability in highly degenerate or large-scale settings. For problems requiring exact vertex identification, Simplex maintains superior precision, while Interior Point excels in overall solution accuracy for complex models.
Applicability in Large-Scale Problems
Interior point methods excel in solving large-scale linear programming problems due to their polynomial-time complexity and ability to handle sparse constraint matrices efficiently. Simplex algorithms, while effective for medium-scale problems, often face performance degradation as problem size increases because of their exponential worst-case time complexity. For extensive optimization tasks, interior point methods provide more reliable scalability and computational efficiency.
Use Cases and Industry Applications
The Interior Point method excels in large-scale linear optimization problems common in telecommunications and energy grid management due to its polynomial-time performance and scalability. The Simplex method remains preferred in industries like manufacturing and transportation where problem sizes are moderate and solution interpretability is crucial, offering precise vertex-based solutions. Financial modeling and supply chain optimization often leverage both methods to balance computational efficiency and solution accuracy depending on problem complexity and real-time requirements.
Advantages and Disadvantages of Each Method
The Interior Point method excels in handling large-scale linear programming problems by providing polynomial-time convergence and better performance with sparse matrices, though it may require more complex implementation and struggle with finding exact basic feasible solutions. The Simplex method offers intuitive geometric interpretation and precise vertex solutions, making it effective for smaller problems and sensitivity analyses, despite its exponential worst-case time complexity and potential inefficiency on very large problems. Choosing between Interior Point and Simplex depends heavily on problem size, sparsity, and the need for exact solution characterization.
Choosing the Best Algorithm for Your Problem
Choosing between Interior Point and Simplex algorithms depends on problem size and structure; Interior Point methods excel in large-scale linear programming with dense constraints, providing polynomial-time convergence. Simplex is preferred for small to medium-sized problems or situations requiring detailed vertex-by-vertex solutions due to its combinatorial nature and ease of implementation. Assessing factors like computational resources, problem sparsity, and solution precision guides selecting the most efficient algorithm.
Interior Point Infographic
 libterm.com
libterm.com