Morphism is a fundamental concept in mathematics and computer science, describing structure-preserving mappings between objects in categories, such as sets, groups, or topological spaces. Understanding morphisms helps you analyze relationships and transformations within complex systems, making it easier to apply abstract theory to practical problems. Explore the rest of this article to discover how morphisms shape various fields and enhance your mathematical toolkit.
Table of Comparison
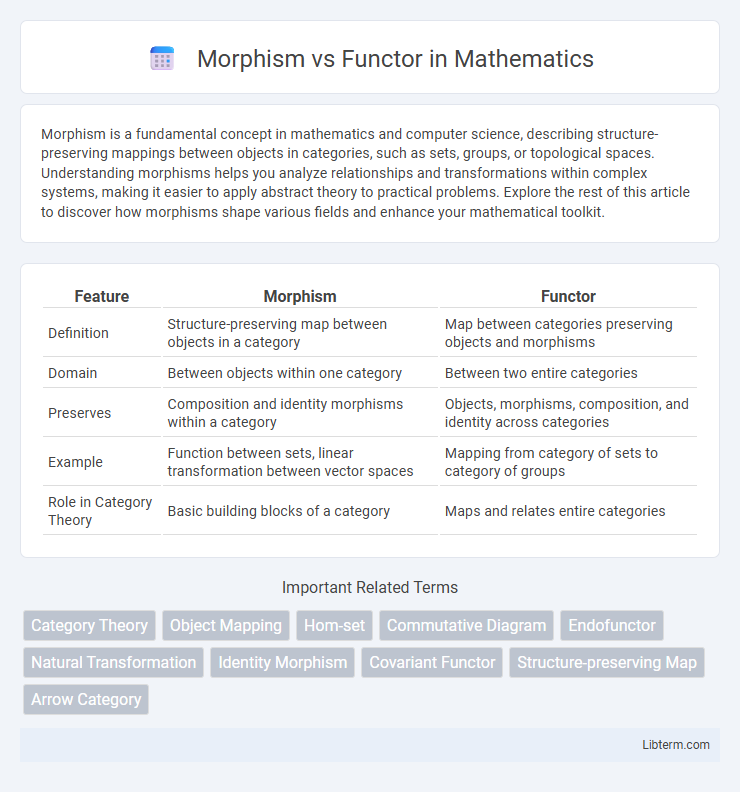
| Feature | Morphism | Functor |
|---|---|---|
| Definition | Structure-preserving map between objects in a category | Map between categories preserving objects and morphisms |
| Domain | Between objects within one category | Between two entire categories |
| Preserves | Composition and identity morphisms within a category | Objects, morphisms, composition, and identity across categories |
| Example | Function between sets, linear transformation between vector spaces | Mapping from category of sets to category of groups |
| Role in Category Theory | Basic building blocks of a category | Maps and relates entire categories |
Understanding the Basics: Morphism and Functor
Morphism in category theory represents a structure-preserving map between two objects, capturing the essential relationships within a category. A functor acts as a mapping between categories, translating objects and morphisms from one category to another while preserving composition and identity structures. Understanding morphisms and functors is fundamental for grasping how mathematical structures and their transformations interact across different categories.
Defining Morphisms in Category Theory
Morphisms in category theory serve as the fundamental arrows representing structure-preserving mappings between objects within a category, capturing the essence of transformations. Unlike functors, which map between categories by assigning objects and morphisms from one category to another while preserving composition and identities, morphisms reside within a single category and focus on relationships between individual objects. Defining morphisms involves specifying their domain and codomain objects along with composition rules that satisfy associativity and identity properties, forming the backbone of categorical structure.
What is a Functor? An Overview
A functor is a mapping between categories that preserves the structure of objects and morphisms, ensuring that composition and identity morphisms remain consistent across categories. It assigns to each object in the source category an object in the target category and to each morphism in the source category a morphism in the target category, satisfying functoriality conditions. Functors play a fundamental role in category theory by enabling the translation of mathematical concepts and constructions from one category to another while maintaining their inherent relationships.
The Role of Morphisms in Mathematical Structures
Morphisms serve as structure-preserving maps between objects in categories, enabling the formal comparison and transformation of mathematical structures such as groups, rings, and topological spaces. In contrast, functors act as mappings between categories that assign objects and morphisms in one category to objects and morphisms in another while preserving composition and identity mappings. The critical role of morphisms lies in maintaining structural integrity during these transformations, thereby facilitating the study of algebraic and geometric properties through categorical frameworks.
Functors: Bridging Categories
Functors serve as structure-preserving maps between categories, translating objects and morphisms from one category to another while maintaining compositional identity. By mapping each object in the source category to an object in the target category and each morphism to a morphism, functors facilitate the transfer of categorical properties and relationships. This bridging role enables comparisons, constructions, and transformations across different categorical contexts, forming the backbone of category theory applications in mathematics and computer science.
Key Differences Between Morphisms and Functors
Morphism in category theory refers to arrows or structure-preserving maps between objects within the same category, while functors are mappings between categories that preserve the composition and identity of morphisms. Key differences include that morphisms operate at the object level within one category, whereas functors map entire categories, including both objects and morphisms, to another category. Morphisms preserve the internal structure of objects, while functors preserve the overall categorical structure, maintaining compositions and identities across categories.
Examples of Morphisms in Practice
Morphism examples in practice include functions between sets, such as f: X - Y mapping elements from set X to set Y, and linear transformations between vector spaces, which preserve vector addition and scalar multiplication. In the category of groups, group homomorphisms serve as morphisms that maintain group operations structurally. These practical morphisms demonstrate the fundamental role of mappings respecting structure in different mathematical contexts.
Real-World Applications of Functors
Functors serve as powerful abstractions in functional programming and category theory, enabling the mapping of data structures while preserving their context and composition rules, unlike morphisms which represent structure-preserving maps between objects. Real-world applications of functors are evident in data manipulation tasks within languages like Haskell and Scala, where they facilitate operations on wrapped values such as lists, options, or futures without unpacking them. This abstraction streamlines complex transformations in software development, enhances code reusability, and supports the implementation of design patterns like the iterator or observer.
Interplay Between Morphisms and Functors
Morphisms represent structure-preserving maps between objects within a category, while functors act as mappings between categories, translating objects and morphisms from one category to another. The interplay between morphisms and functors is crucial because functors must respect morphism composition and identities, ensuring that the categorical structure remains intact under the mapping. This relationship enables the transfer of algebraic and topological properties across different categories, facilitating deeper analysis in category theory.
Conclusion: Choosing Morphism or Functor for Your Needs
Selecting between morphisms and functors depends on the complexity of transformations required; morphisms effectively capture simple structure-preserving maps within a single category, while functors handle mappings across entire categories, preserving structures at a higher level. Morphisms are suitable for localized operations within algebraic or topological structures, whereas functors enable systematic translation between categories, facilitating broader mathematical or computational frameworks. Understanding the scope and scale of your problem guides the choice, ensuring precise and efficient abstraction through either morphisms or functors.
Morphism Infographic
 libterm.com
libterm.com