Small cardinals are vibrant birds known for their striking red plumage and melodious songs, often found in woodlands and gardens. Their agile movements and distinctive calls make them a favorite among birdwatchers and nature enthusiasts. Discover more fascinating facts about small cardinals and how you can spot them in the wild by reading the full article.
Table of Comparison
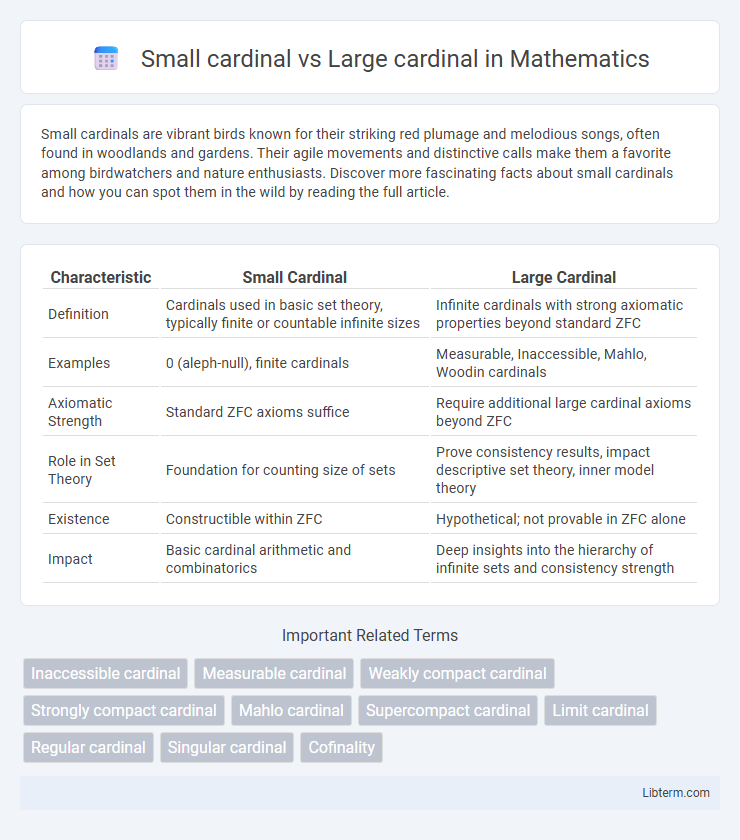
| Characteristic | Small Cardinal | Large Cardinal |
|---|---|---|
| Definition | Cardinals used in basic set theory, typically finite or countable infinite sizes | Infinite cardinals with strong axiomatic properties beyond standard ZFC |
| Examples | 0 (aleph-null), finite cardinals | Measurable, Inaccessible, Mahlo, Woodin cardinals |
| Axiomatic Strength | Standard ZFC axioms suffice | Require additional large cardinal axioms beyond ZFC |
| Role in Set Theory | Foundation for counting size of sets | Prove consistency results, impact descriptive set theory, inner model theory |
| Existence | Constructible within ZFC | Hypothetical; not provable in ZFC alone |
| Impact | Basic cardinal arithmetic and combinatorics | Deep insights into the hierarchy of infinite sets and consistency strength |
Introduction to Cardinals in Set Theory
Small cardinals refer to well-known infinite cardinal numbers such as 0 (aleph-null), representing the size of countable sets like the natural numbers. Large cardinals extend beyond these, embodying strong axioms of infinity with properties that imply the existence of vast and structurally rich infinite sets, often serving as milestones in the hierarchy of infinite sizes. Understanding the distinction between small and large cardinals is fundamental in set theory for exploring the foundations of mathematics and the nature of infinite sets.
Defining Small Cardinals
Small cardinals are infinite cardinal numbers that lie within the initial hierarchy of cardinalities, typically including aleph-null (0), aleph-one (1), and their successors, which correspond to countable and somewhat larger infinite sets. They are defined by their role in set theory as basic measures of infinity without invoking strong axioms of infinity or large cardinal properties. Unlike large cardinals, which exhibit strong combinatorial or consistency strength properties beyond ZFC, small cardinals serve as foundational building blocks for understanding the size of infinite sets in standard mathematical frameworks.
Understanding Large Cardinals
Large cardinals represent an advanced class of infinite cardinal numbers characterized by strong consistency and powerful combinatorial properties that extend beyond those of small cardinals such as aleph-null or aleph-one. These cardinals are pivotal in set theory because they often imply the existence of rich mathematical structures and serve as hypotheses for proving the consistency of various axioms. Understanding large cardinals involves exploring their hierarchy, including measurable, supercompact, and huge cardinals, each defined by progressively stronger embedding properties and reflecting levels of infinity that transcend standard transfinite cardinalities.
Historical Development of Cardinal Hierarchies
The historical development of cardinal hierarchies began with the introduction of small cardinals, which include finite and basic infinite cardinals like aleph-null (0), representing the size of natural numbers. Large cardinals emerged as a more complex concept during the 20th century, driven by set theorists such as Kurt Godel and Paul Cohen, who explored cardinals with stronger axiomatic properties like measurable, inaccessible, and supercompact cardinals. These large cardinals play a crucial role in understanding the foundations of mathematics by extending the hierarchy and providing deep insights into the structure of the set-theoretic universe.
Key Differences Between Small and Large Cardinals
Small cardinals refer to cardinal numbers less than or equal to 0 (aleph-null), representing the sizes of finite or countably infinite sets, while large cardinals transcend standard set theory axioms, exhibiting strong combinatorial properties and consistency strength beyond ZFC (Zermelo-Fraenkel set theory with the axiom of choice). The key differences lie in their foundational role: small cardinals measure basic set sizes and are well-understood within standard mathematics, whereas large cardinals imply the existence of more complex infinities, often asserting strong hypotheses independent of and extending standard axioms. Large cardinals include measurable, supercompact, and huge cardinals, which influence the structure of the set-theoretic universe and have profound implications for consistency and hierarchy, unlike small cardinals that serve as fundamental building blocks for counting and ordering sets.
Role of Small Cardinals in Mathematics
Small cardinals such as 0 (aleph-null) play a fundamental role in set theory and foundational mathematics by representing countable infinities crucial for defining sequences, functions, and structures in analysis and topology. They establish the baseline hierarchy for infinite sets, enabling mathematicians to classify and compare sizes of infinite collections before progressing to large cardinals that encode stronger consistency and combinatorial properties. Small cardinals are essential in understanding concepts like countability, ordinal numbers, and the structure of the real line, forming the groundwork upon which more complex large cardinal axioms build.
Impact of Large Cardinals on Set Theory Axioms
Large cardinals extend the standard Zermelo-Fraenkel axioms by positing the existence of infinitely large infinite sets with strong structural properties, which profoundly influence consistency and independence results in set theory. Their assumptions lead to refined hierarchies and enable the resolution of statements undecidable by ZFC alone, thereby shaping the foundational landscape. In contrast, small cardinals correspond to more accessible infinite magnitudes with less impact on foundational axioms and consistency strength.
Applications and Implications in Mathematical Logic
Small cardinals, such as aleph-null (0) and aleph-one (1), play a crucial role in descriptive set theory and model theory by providing frameworks to analyze countable structures and definability properties. Large cardinals, including inaccessible, measurable, and supercompact cardinals, have profound applications in consistency proofs and the development of inner model theory, influencing foundational aspects like determinacy and forcing axioms. The implications of large cardinals extend to the hierarchy of mathematical universes, affecting the classification of sets and the exploration of independence results beyond ZFC (Zermelo-Fraenkel set theory with the Axiom of Choice).
Open Problems and Research Directions
Open problems in small and large cardinal theory include the exploration of the precise consistency strength relationships between various large cardinal axioms such as Woodin cardinals, supercompact cardinals, and strong inaccessible cardinals. Research directions emphasize determining the boundary between consistency and inconsistency of combinatorial principles derived from small cardinal assumptions versus the structural hierarchy imposed by large cardinal hypotheses. Investigating the interaction between forcing techniques and inner model theory continues to provide deep insights into unresolved questions about large cardinal embeddings and definability properties.
Conclusion: The Significance of Cardinal Distinctions
Small cardinals represent foundational infinite sizes with properties crucial for basic set theory, while large cardinals embody stronger axioms extending beyond standard frameworks, often implying profound consistency and structural insights. The distinction between small and large cardinals underscores their role in organizing the hierarchy of infinite sets, influencing the development of mathematical logic and the understanding of set-theoretic universes. Recognizing these cardinal differences enhances comprehension of the logical landscape, highlighting the interplay between consistency strength and the foundational underpinnings of mathematics.
Small cardinal Infographic
 libterm.com
libterm.com