A non-injective function maps two or more distinct elements from its domain to the same element in its codomain, causing a loss of uniqueness in output values. This property contrasts with injective functions where each input corresponds to a distinct output, which is crucial in fields like cryptography and data compression. Explore the rest of the article to deepen your understanding of non-injective functions and their applications.
Table of Comparison
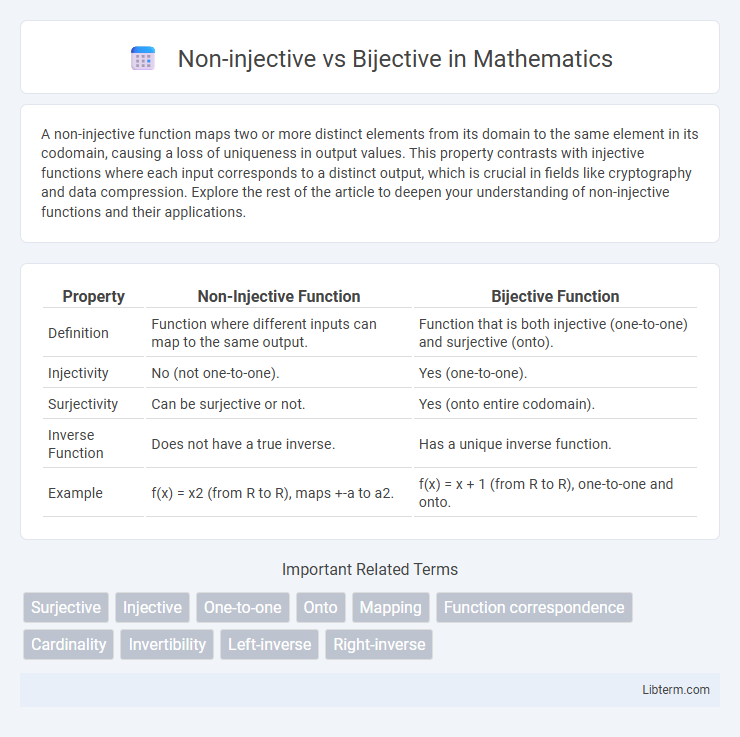
| Property | Non-Injective Function | Bijective Function |
|---|---|---|
| Definition | Function where different inputs can map to the same output. | Function that is both injective (one-to-one) and surjective (onto). |
| Injectivity | No (not one-to-one). | Yes (one-to-one). |
| Surjectivity | Can be surjective or not. | Yes (onto entire codomain). |
| Inverse Function | Does not have a true inverse. | Has a unique inverse function. |
| Example | f(x) = x2 (from R to R), maps +-a to a2. | f(x) = x + 1 (from R to R), one-to-one and onto. |
Introduction to Function Types: Non-injective and Bijective
Non-injective functions map at least two distinct elements of the domain to the same element in the codomain, lacking one-to-one correspondence. Bijective functions establish a perfect pairing by being both injective and surjective, ensuring every element in the codomain corresponds to exactly one element in the domain. Understanding the distinction between non-injective and bijective functions is crucial for grasping function invertibility and mapping behavior in mathematical analysis and set theory.
Defining Injectivity: What Makes a Function Non-injective?
A function is non-injective if there exists at least one pair of distinct inputs that map to the same output, violating the property of injectivity where each input corresponds to a unique output. Non-injective functions fail to provide a one-to-one relationship, causing some outputs to have multiple pre-images. This contrasts with bijective functions, which are both injective and surjective, ensuring a perfect one-to-one correspondence between domain and codomain elements.
The Concept of Bijectivity: One-to-One and Onto
Bijectivity is characterized by a function being both one-to-one (injective) and onto (surjective), ensuring every element in the codomain is uniquely paired with an element in the domain. Non-injective functions lack this one-to-one property, allowing multiple domain elements to map to the same codomain element, which prevents establishing a perfect pairing between sets. The concept of bijectivity is fundamental in fields like set theory and linear algebra, enabling invertible functions and establishing equivalences between mathematical structures.
Visual Representations: Graphical Differences
Non-injective functions exhibit overlapping outputs in their graphical representations, where multiple inputs map to the same output value, leading to horizontal line tests that intersect the graph at more than one point. Bijective functions, by contrast, display a one-to-one correspondence between inputs and outputs, ensuring that each output is uniquely paired with an input, visually confirmed by graphs passing both vertical and horizontal line tests exactly once. These graphical differences highlight the overlapping mappings in non-injective functions versus the perfect pairing in bijections, crucial for understanding function invertibility and uniqueness.
Real-world Examples of Non-injective Functions
Non-injective functions map multiple inputs to a single output, such as the squaring function f(x) = x2, where both 2 and -2 yield 4, illustrating ambiguity in reverse mapping. In real-world scenarios, non-injective behavior appears in temperature conversions from Celsius to Fahrenheit at certain points or in hashing algorithms where different data inputs produce identical hash codes, causing collisions. These examples demonstrate the importance of understanding function injectivity for applications in data compression, cryptography, and signal processing.
Practical Applications of Bijective Functions
Bijective functions have crucial practical applications in cryptography, where their one-to-one and onto properties ensure secure encryption and decryption processes by uniquely mapping plaintext to ciphertext and vice versa. In database systems, bijective mappings enable reliable data retrieval by establishing a perfect correspondence between keys and records, eliminating ambiguity or data loss. Moreover, bijections are fundamental in combinatorics and algorithms, facilitating reversible transformations that preserve structure and allow for efficient problem-solving and data manipulation.
Mathematical Properties: Comparing Non-injective and Bijective Functions
Non-injective functions map at least two distinct elements from the domain to the same element in the codomain, resulting in a lack of one-to-one correspondence. Bijective functions establish a perfect one-to-one and onto relationship between domain and codomain, ensuring that every element in the codomain is paired with exactly one unique element from the domain. This bijection guarantees invertibility, while non-injective functions do not possess a well-defined inverse due to their overlapping mappings.
Implications in Set Theory and Mapping
Non-injective functions allow multiple elements in the domain to map to a single element in the codomain, which complicates the establishment of one-to-one correspondences between sets and affects the uniqueness of inverse mappings. Bijective functions establish a perfect pairing between elements of the domain and codomain, ensuring both injectivity and surjectivity, which guarantees the existence of an inverse function and supports set equivalence in cardinality comparisons. In set theory, bijections are critical for defining isomorphisms between sets, preserving structure and enabling precise mapping across mathematical objects.
Non-injective vs Bijective: Key Distinctions and Consequences
Non-injective functions map at least two distinct elements from the domain to the same element in the codomain, resulting in a lack of one-to-one correspondence. Bijective functions establish a perfect pairing between every element in the domain and a unique element in the codomain, ensuring both injectivity and surjectivity. The key consequence of a function being non-injective is the impossibility of defining a unique inverse function, whereas bijective functions guarantee invertibility and a reversible mapping.
Summary and Importance in Mathematical Analysis
Non-injective functions map multiple elements of the domain to a single element in the codomain, losing information about the original input and complicating reverse mappings, whereas bijective functions establish a perfect one-to-one correspondence between domain and codomain, ensuring invertibility and structural symmetry. In mathematical analysis, understanding these distinctions is crucial for function classification, determining the existence of inverse functions, and analyzing transformations in vector spaces and topology. The bijective property guarantees that every output has a unique input, facilitating precise manipulations and proofs in advanced mathematical contexts.
Non-injective Infographic
 libterm.com
libterm.com