Norms establish consistent standards and expectations that guide behavior and processes across various contexts, ensuring harmony and predictability. Understanding the role of norms is essential for adapting to social, professional, and cultural environments seamlessly. Explore the full article to discover how norms influence your interactions and decision-making.
Table of Comparison
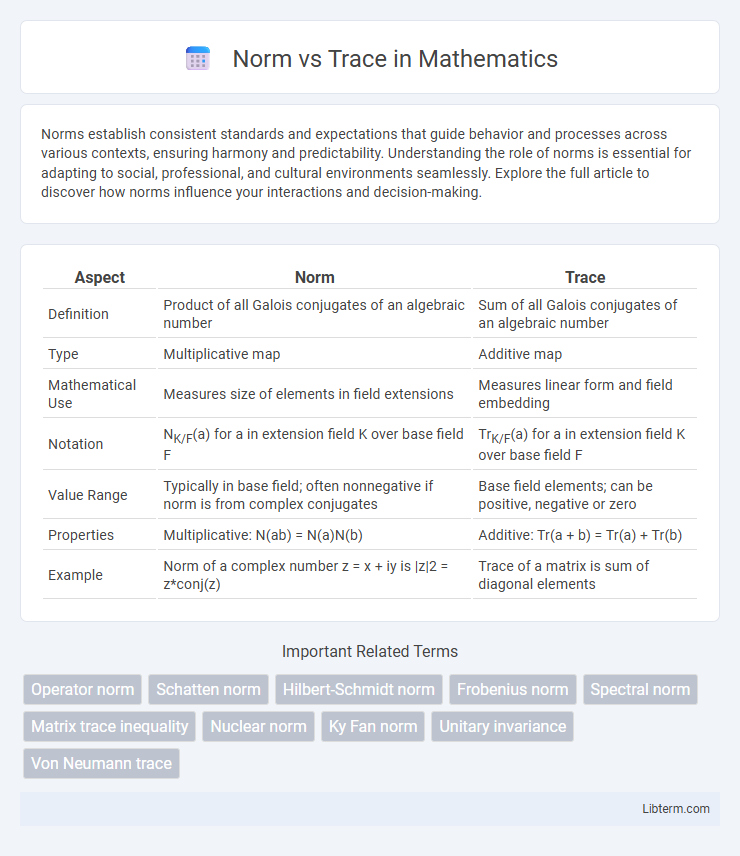
| Aspect | Norm | Trace |
|---|---|---|
| Definition | Product of all Galois conjugates of an algebraic number | Sum of all Galois conjugates of an algebraic number |
| Type | Multiplicative map | Additive map |
| Mathematical Use | Measures size of elements in field extensions | Measures linear form and field embedding |
| Notation | NK/F(a) for a in extension field K over base field F | TrK/F(a) for a in extension field K over base field F |
| Value Range | Typically in base field; often nonnegative if norm is from complex conjugates | Base field elements; can be positive, negative or zero |
| Properties | Multiplicative: N(ab) = N(a)N(b) | Additive: Tr(a + b) = Tr(a) + Tr(b) |
| Example | Norm of a complex number z = x + iy is |z|2 = z*conj(z) | Trace of a matrix is sum of diagonal elements |
Introduction to Norm and Trace
Norm and trace are fundamental concepts in linear algebra and field theory, particularly in the study of field extensions and matrix operations. The norm of an element in a field extension is defined as the determinant of the linear transformation representing multiplication by that element, reflecting its multiplicative impact across the extension. The trace, on the other hand, equals the sum of the eigenvalues of the same transformation, capturing the additive effect and playing a crucial role in characterizing field automorphisms and algebraic integers.
Definitions: Norm vs Trace
The norm of an element in a field extension is the product of all its Galois conjugates, producing a value in the base field that reflects multiplicative structure. The trace of an element is defined as the sum of all its Galois conjugates, capturing additive properties within the extension. Both norm and trace serve as critical tools in algebraic number theory and field theory for characterizing elements via their embeddings into larger fields.
Mathematical Background of Norm
The mathematical background of the norm involves its definition as a function that assigns a strictly positive length or size to all vectors in a vector space, except for the zero vector. Norms satisfy properties such as positive definiteness, homogeneity, and the triangle inequality, which are fundamental in analysis and linear algebra. Unlike the trace, which is the sum of diagonal elements of a matrix, the norm quantifies the magnitude of vectors or operators and plays a crucial role in studying vector space topology and stability.
Mathematical Background of Trace
The trace of a matrix is the sum of its diagonal elements, representing the sum of its eigenvalues with multiplicities, and it is a linear functional on the space of square matrices. It plays a fundamental role in various branches of mathematics, including linear algebra, tensor analysis, and trace operator theory, by providing insights into matrix similarity and spectral properties. The trace is invariant under cyclic permutations and is often used to calculate matrix norms and related invariants, linking it closely to the matrix's spectral norm and Frobenius norm.
Key Differences Between Norm and Trace
The key differences between norm and trace arise from their definitions in linear algebra: the norm of a vector measures its length or magnitude in a vector space, typically using Euclidean distance, while the trace of a square matrix is the sum of its diagonal elements, representing the sum of eigenvalues. Norms provide quantitative measures for vector size and can be extended to matrices as operator norms, whereas the trace is a scalar value reflecting matrix properties like invariance under similarity transformations. Norms are used in optimization and error measurement, while trace is pivotal in matrix theory, spectral analysis, and quantum mechanics.
Properties of Matrix Norms
Matrix norms satisfy key properties including positivity, scalability, and the triangle inequality, ensuring consistent measurement of matrix size. The trace, defined as the sum of diagonal elements, behaves linearly but does not fulfill norm properties like submultiplicativity or definiteness. Unlike the trace, matrix norms such as the Frobenius norm or spectral norm provide comprehensive bounds on matrix behavior in vector spaces and support stability analysis in numerical methods.
Properties of Matrix Trace
The trace of a matrix, defined as the sum of its diagonal elements, is a linear operator that remains invariant under cyclic permutations, making it essential in characterizing matrix similarity and eigenvalues. Unlike norms, the trace is not a measure of magnitude but a scalar value with properties such as linearity (Tr(A + B) = Tr(A) + Tr(B)) and invariance under transposition (Tr(A) = Tr(AT)). These properties distinguish the trace in applications involving matrix derivatives, spectral theory, and optimization problems where the sum of eigenvalues plays a critical role.
Applications of Norm in Linear Algebra
Norms in linear algebra quantify the size or length of vectors, playing a crucial role in vector space analysis, optimization, and numerical stability. Their applications include measuring distances between points, evaluating convergence in iterative algorithms, and normalizing vectors in machine learning models. Common norms such as the Euclidean norm, p-norm, and infinity norm facilitate solutions of linear systems, error estimation, and matrix conditioning.
Applications of Trace in Linear Algebra
Trace is widely used in linear algebra for matrix analysis, including determining properties such as eigenvalue sums and invariants under similarity transformations. It plays a critical role in solving systems of linear equations, evaluating matrix functions, and studying linear transformations in vector spaces. Applications extend to fields like quantum mechanics and statistics, where the trace helps characterize operators and covariance matrices.
Summary: Choosing Norm or Trace
Norm and trace function as crucial metrics in linear algebra and matrix analysis, with the norm measuring the magnitude or size of a matrix and the trace summing its diagonal elements to reflect characteristics such as eigenvalue sums. Selecting between norm and trace depends on the application: norms are preferred for assessing matrix stability, error bounds, or convergence properties, while trace is suitable for capturing aggregate properties like total variance or expected values in quantum mechanics and statistics. Understanding the specific analytical goal guides the optimal choice--norms excel in bounding behavior and sensitivity, whereas trace offers concise spectral summarization.
Norm Infographic
 libterm.com
libterm.com