The monodromy group captures how solutions to differential equations or analytic functions behave when analytically continued along paths around singularities, revealing the intrinsic symmetries of the problem. Understanding this group helps in classifying covers, solving polynomial equations, and studying complex algebraic structures. Dive into the rest of the article to explore the fundamental concepts and applications of the monodromy group in depth.
Table of Comparison
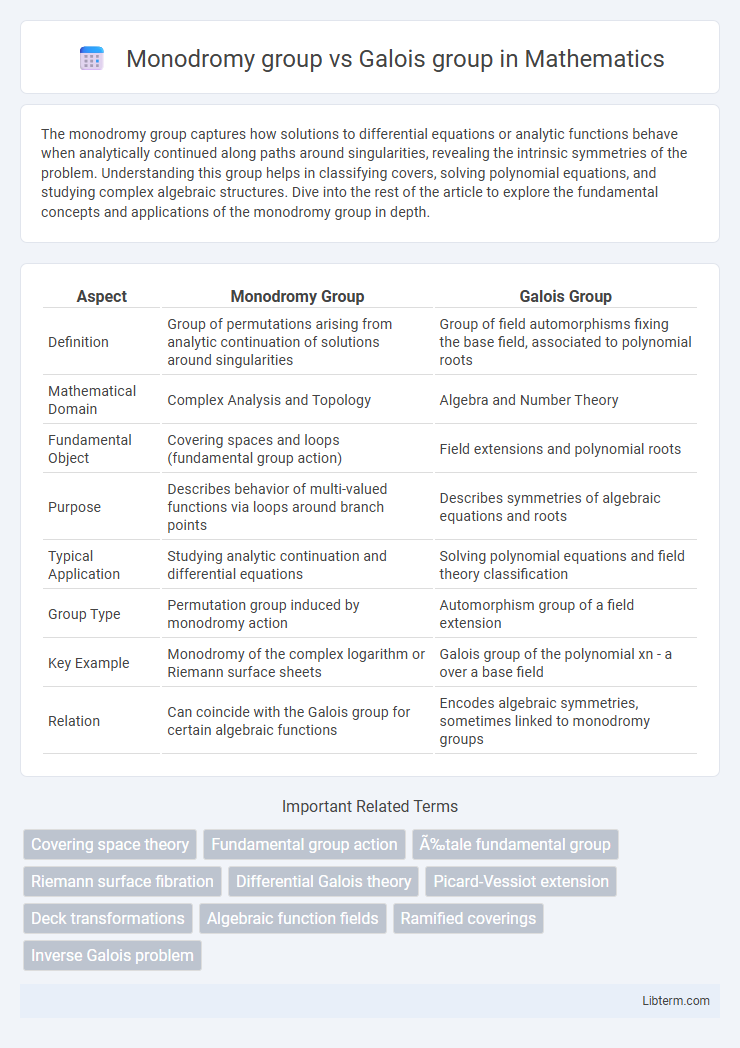
| Aspect | Monodromy Group | Galois Group |
|---|---|---|
| Definition | Group of permutations arising from analytic continuation of solutions around singularities | Group of field automorphisms fixing the base field, associated to polynomial roots |
| Mathematical Domain | Complex Analysis and Topology | Algebra and Number Theory |
| Fundamental Object | Covering spaces and loops (fundamental group action) | Field extensions and polynomial roots |
| Purpose | Describes behavior of multi-valued functions via loops around branch points | Describes symmetries of algebraic equations and roots |
| Typical Application | Studying analytic continuation and differential equations | Solving polynomial equations and field theory classification |
| Group Type | Permutation group induced by monodromy action | Automorphism group of a field extension |
| Key Example | Monodromy of the complex logarithm or Riemann surface sheets | Galois group of the polynomial xn - a over a base field |
| Relation | Can coincide with the Galois group for certain algebraic functions | Encodes algebraic symmetries, sometimes linked to monodromy groups |
Introduction to Monodromy and Galois Groups
Monodromy groups arise in the study of analytic continuation of multivalued functions around singularities, capturing how function values permute when loops encircle branch points. Galois groups represent symmetries of roots of polynomial equations, encoding field extension automorphisms that fix the base field. Both groups reveal deep connections between algebraic and geometric structures, with monodromy groups linking to topological properties and Galois groups to algebraic solvability.
Historical Background and Mathematical Context
The monodromy group originated in the study of analytic continuation of multivalued functions in complex analysis, first formalized by Emile Picard in the late 19th century, while the Galois group emerged from Evariste Galois's work on polynomial solvability in the early 19th century. Both groups serve to understand symmetries: the monodromy group captures how analytic continuation around singularities permutes function branches, and the Galois group describes field automorphisms fixing a base field related to polynomial roots. Their interplay appears prominently in algebraic geometry and differential equations, linking topological properties of covering spaces with algebraic structures governing solution behavior.
Fundamental Concepts: Covering Spaces and Field Extensions
The monodromy group arises from the action of the fundamental group on the fibers of a covering space, capturing how loops in the base space permute these fibers. The Galois group, in contrast, is defined through field extensions as the group of automorphisms of an extension field that fix the base field, encoding algebraic symmetries of polynomial roots. Both groups reflect symmetry: monodromy governs topological coverings, while Galois groups structure algebraic extensions, linking topology with field theory.
Definition and Construction of the Monodromy Group
The Monodromy group arises from the study of analytic continuation of multivalued functions along loops in a punctured complex plane, capturing how function values permute when encircling branch points. This group is constructed by associating elements of the fundamental group of the punctured base space with permutations of the fiber over a base point, revealing the topological action on function branches. In contrast, the Galois group is defined algebraically as the group of field automorphisms fixing a base field, encoding symmetries of roots of polynomials, while the Monodromy group emphasizes geometric and topological transformations.
Definition and Construction of the Galois Group
The Galois group of a polynomial is defined as the group of field automorphisms of its splitting field that fix the base field, capturing the symmetries of the roots through algebraic field extensions. Its construction involves identifying automorphisms that permute the roots and maintain the structure of the base field, establishing a connection between field theory and group theory. Contrarily, the monodromy group arises from the analytic continuation of solutions to differential equations or algebraic functions around singularities, representing topological rather than purely algebraic symmetries.
Geometric Interpretation: Monodromy in Topology
The monodromy group captures how solutions of a branched covering space permute when analytically continued along loops around branch points, reflecting the fundamental group action on fiber sheets. This topological viewpoint contrasts with the Galois group, which algebraically encodes field automorphisms fixing the base field in a polynomial extension. Monodromy reveals the geometric structure of covering spaces via path-lifting properties, linking algebraic and topological aspects in complex geometry.
Algebraic Interpretation: Galois Theory and Polynomial Equations
The Galois group of a polynomial is the group of field automorphisms of its splitting field that fix the base field, encoding symmetries of the roots and governing the solvability of polynomial equations by radicals. The monodromy group arises from analytic continuation of the roots along loops around branch points, reflecting topological symmetries linked to the algebraic structure of the polynomial's solutions. Both groups provide distinct but interrelated algebraic interpretations in Galois theory: the Galois group captures field-theoretic automorphisms, while the monodromy group connects to geometric and analytic properties of polynomial equations.
Key Differences Between Monodromy and Galois Groups
Monodromy groups arise from the analytic continuation of multivalued functions around singularities, capturing the permutation of function branches, while Galois groups describe symmetries of field extensions and polynomial roots in algebraic structures. The monodromy group is fundamentally a topological and geometric construct linked to covering spaces and fundamental groups, whereas the Galois group is an algebraic entity associated with field automorphisms preserving algebraic relations. Key differences include their origins--analytic continuation versus algebraic field theory--and their applications, with monodromy groups used in complex analysis and differential equations, and Galois groups central to solving polynomial equations and understanding field extensions.
Connections and Analogies in Modern Mathematics
Monodromy groups and Galois groups both describe symmetries arising from algebraic structures, with monodromy groups encoding the behavior of analytic continuation around singularities and Galois groups capturing field extension automorphisms. In modern mathematics, these groups connect through the study of differential equations, algebraic geometry, and number theory, where monodromy representations relate to covering spaces and local systems, while Galois theory provides fundamental insights into polynomial solvability and arithmetic geometry. Analogies between them emerge in the formulation of the inverse Galois problem and Riemann-Hilbert correspondence, bridging topological and algebraic perspectives on symmetry and structure.
Applications and Further Directions in Algebra and Geometry
Monodromy groups play a crucial role in algebraic geometry by describing how fiber structures vary in families of algebraic varieties, enabling the study of topological and geometric properties of parameter spaces. Galois groups, central in field theory and algebra, capture symmetries of field extensions and solve polynomial equations, offering profound insights into solvability and arithmetic properties. Their interplay guides advanced research in topics like moduli spaces, deformation theory, and the inverse Galois problem, fostering new directions in understanding algebraic structures through geometric and topological lenses.
Monodromy group Infographic
 libterm.com
libterm.com