Injective resolution is a fundamental concept in homological algebra used to study modules by embedding them into injective modules. This process helps analyze complex algebraic structures and compute derived functors such as Ext and sheaf cohomology. Dive deeper into the article to understand how injective resolutions facilitate solving extension problems and reveal deeper module properties.
Table of Comparison
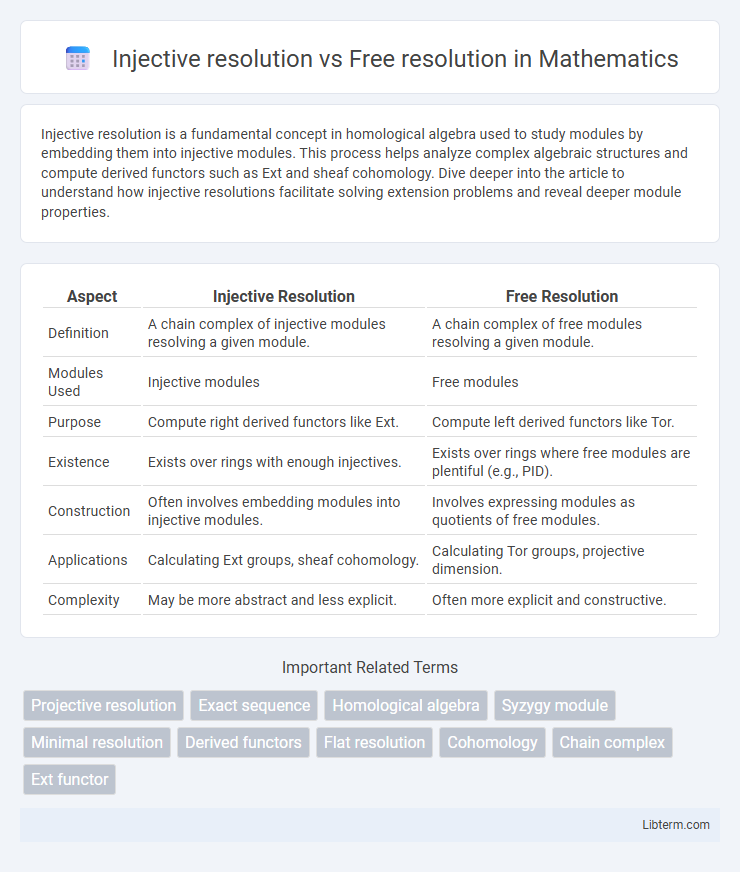
| Aspect | Injective Resolution | Free Resolution |
|---|---|---|
| Definition | A chain complex of injective modules resolving a given module. | A chain complex of free modules resolving a given module. |
| Modules Used | Injective modules | Free modules |
| Purpose | Compute right derived functors like Ext. | Compute left derived functors like Tor. |
| Existence | Exists over rings with enough injectives. | Exists over rings where free modules are plentiful (e.g., PID). |
| Construction | Often involves embedding modules into injective modules. | Involves expressing modules as quotients of free modules. |
| Applications | Calculating Ext groups, sheaf cohomology. | Calculating Tor groups, projective dimension. |
| Complexity | May be more abstract and less explicit. | Often more explicit and constructive. |
Introduction to Injective and Free Resolutions
Injective resolutions and free resolutions are fundamental concepts in homological algebra used to study module structures over rings. An injective resolution of a module involves embedding the module into a sequence of injective modules, which are modules where every exact sequence splits, enabling Ext functor computations. In contrast, a free resolution expresses a module as the cokernel of a chain complex of free modules, which are projective and easier to handle for computing Tor functors and homological dimensions.
Basic Concepts: Modules and Resolutions
Injective resolutions involve expressing a module as a submodule of an injective module chain, facilitating the computation of right-derived functors such as Ext. Free resolutions represent a module through an exact sequence of free modules, providing a concrete framework to analyze projective properties and compute homological invariants like Tor. Both resolutions serve as fundamental tools in homological algebra to study module structure and derive functorial information.
What is a Free Resolution?
A Free Resolution in homological algebra is an exact sequence of free modules used to study the structure of a given module by expressing it as the cokernel of a chain of free modules. It provides a powerful tool for computing homological invariants such as projective dimension and Tor groups. Unlike Injective Resolutions that use injective modules, Free Resolutions emphasize constructing modules from well-understood free bases, facilitating explicit calculations.
What is an Injective Resolution?
An Injective Resolution is an exact sequence of modules and injective homomorphisms that serves to embed a given module into a sequence of injective modules, facilitating the computation of right derived functors in homological algebra. Unlike Free Resolutions, which involve projective or free modules and are used for computing left derived functors, Injective Resolutions help analyze properties related to Ext and sheaf cohomology. Injective modules possess the property that every homomorphism from a submodule can be extended to the whole module, making Injective Resolutions crucial for calculations involving Hom and Ext functors in abelian categories.
Existence Theorems for Resolutions
Injective and free resolutions are fundamental tools in homological algebra for analyzing module properties through exact sequences. The Existence Theorems guarantee that every module over a ring possesses both an injective resolution and a free resolution, ensuring comprehensive coverage in derived functor computations. Injective resolutions allow extension to right-derived functors while free resolutions facilitate left-derived functors, emphasizing their complementary roles in category theory and homological contexts.
Construction Methods: Free vs Injective
Free resolution construction typically involves building a projective chain complex using free modules, often derived from a chosen generating set to simplify homological computations. Injective resolution construction relies on embedding modules into injective modules, employing the Baer criterion or using injective hulls to ensure exactness and facilitate Ext functor calculations. While free resolutions are generally more straightforward in explicit construction due to availability of free modules, injective resolutions demand more intricate embedding techniques but are crucial for dualizing homological dimensions and cohomological studies.
Key Differences Between Injective and Free Resolutions
Injective resolutions involve chain complexes of injective modules used to compute right-derived functors, while free resolutions consist of chain complexes of free modules typically applied to calculate projective dimensions. Injective resolutions are essential in homological algebra for studying Ext groups and cohomology, whereas free resolutions facilitate computations related to Tor groups and projective dimensions. The key difference lies in the type of modules used--injective versus free--which impacts their duality properties and applicability in various derived functor computations.
Homological Applications of Free and Injective Resolutions
Free resolutions facilitate explicit computation of derived functors such as Tor, allowing effective analysis of projective dimension and module structure in homological algebra. Injective resolutions enable the calculation of Ext groups and support deep investigation of cohomological properties, including local cohomology and spectral sequences. Both resolutions serve as fundamental tools for understanding module homology and cohomology, each adapted to different categorical contexts and dual formulations.
Practical Examples and Computation Techniques
Injective resolutions simplify computing right-derived functors such as Ext by embedding modules into injective modules, often used in homological algebra contexts like sheaf cohomology. Free resolutions, constructed from projective modules, facilitate explicit calculations in software like Macaulay2 or SageMath by expressing modules as quotients of free modules, aiding in the computation of Tor and Ext groups. Practical computation often involves balancing between the theoretical clarity of injective resolutions and the algorithmic convenience of free resolutions, especially when working with finitely generated modules over polynomial rings.
Summary: Choosing Between Injective and Free Resolutions
Injective resolutions are essential in homological algebra for computing right derived functors, especially when working with modules over rings with sufficient injectives, while free resolutions provide explicit constructions via projective modules that simplify computations of left derived functors such as Tor. The choice between injective and free resolutions depends on the ring structure and the derived functors of interest, with free resolutions being more practical for constructing projective presentations and injective resolutions advantageous for dealing with extension groups and cohomology. In general, free resolutions are preferred when aiming for explicit, minimal models, whereas injective resolutions excel in abstract homological contexts requiring injective objects and exactness on the right.
Injective resolution Infographic
 libterm.com
libterm.com