Cech cohomology provides a powerful method to study the global properties of topological spaces by analyzing the intersections of open covers. This approach captures essential information about the structure and classification of spaces, particularly in algebraic topology and complex geometry. Explore the rest of the article to deepen your understanding of how Cech cohomology applies to modern mathematical problems.
Table of Comparison
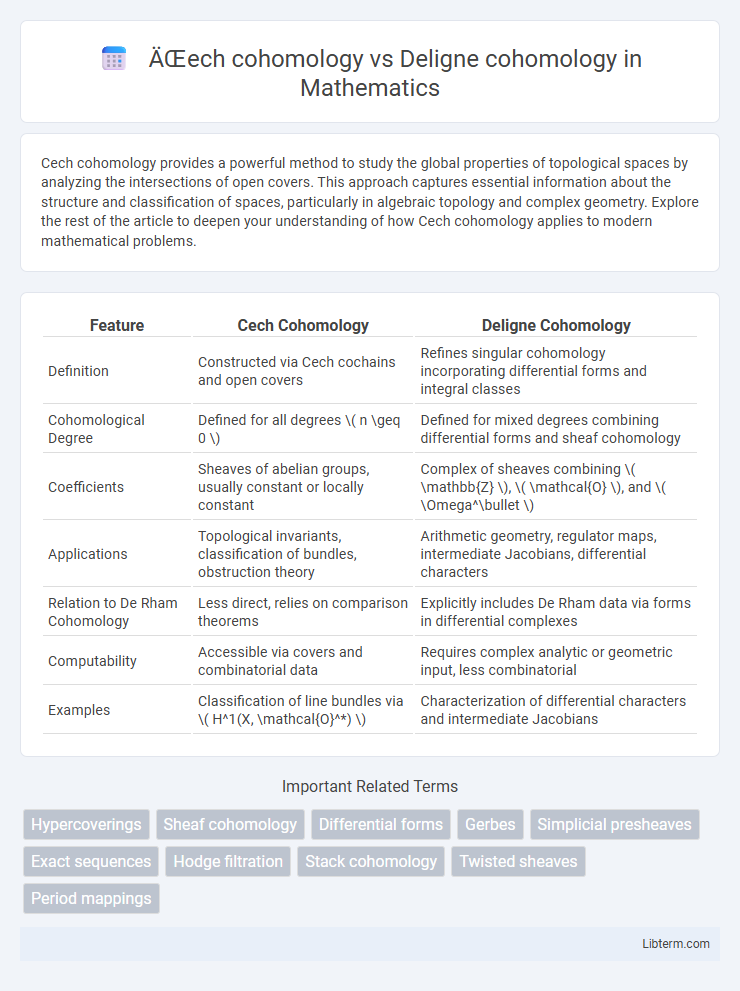
| Feature | Cech Cohomology | Deligne Cohomology |
|---|---|---|
| Definition | Constructed via Cech cochains and open covers | Refines singular cohomology incorporating differential forms and integral classes |
| Cohomological Degree | Defined for all degrees \( n \geq 0 \) | Defined for mixed degrees combining differential forms and sheaf cohomology |
| Coefficients | Sheaves of abelian groups, usually constant or locally constant | Complex of sheaves combining \( \mathbb{Z} \), \( \mathcal{O} \), and \( \Omega^\bullet \) |
| Applications | Topological invariants, classification of bundles, obstruction theory | Arithmetic geometry, regulator maps, intermediate Jacobians, differential characters |
| Relation to De Rham Cohomology | Less direct, relies on comparison theorems | Explicitly includes De Rham data via forms in differential complexes |
| Computability | Accessible via covers and combinatorial data | Requires complex analytic or geometric input, less combinatorial |
| Examples | Classification of line bundles via \( H^1(X, \mathcal{O}^*) \) | Characterization of differential characters and intermediate Jacobians |
Introduction to Čech Cohomology and Deligne Cohomology
Cech cohomology provides a computational approach to sheaf cohomology by using open covers of topological spaces, enabling the study of global sections through local data. Deligne cohomology extends this framework by incorporating differential forms and integral cohomology into a single complex, facilitating applications in arithmetic geometry and the theory of characteristic classes. Both theories reveal deep relationships between topology, algebraic geometry, and category theory, with Cech cohomology emphasizing combinatorial methods and Deligne cohomology blending cohomological and differential geometric structures.
Historical Background and Motivation
Cech cohomology originated in the early 20th century as a tool for classifying topological spaces through open coverings, providing a combinatorial approach to sheaf theory and cohomological invariants. Deligne cohomology emerged in the 1970s, motivated by the need to unify differential and integral cohomological data, particularly in the context of Hodge theory and arithmetic geometry. This refinement extended classical cohomology by incorporating both cocycles and differential forms, enabling more precise classifications of geometric objects and making connections to arithmetic and complex analytic structures.
Foundational Concepts: Sheaves and Covers
Cech cohomology utilizes open covers and presheaves or sheaves to compute cohomological invariants by examining the intersections of these covers, providing a combinatorial framework for cohomology calculations. Deligne cohomology extends this by incorporating sheaves of complexes, typically combining differential forms and local systems, thereby encoding both topological and geometric data such as characteristic classes and holonomy. The foundational difference lies in Cech cohomology's reliance on covers and their nerves, while Deligne cohomology integrates sheaf-theoretic resolutions and the derived category approach to capture refined geometric information.
Čech Cohomology: Definition and Computation
Cech cohomology is a topological tool that computes cohomology groups using an open cover of a topological space and the intersections of these open sets, providing an algebraic invariant for classifying sheaves and continuous functions. Its computation involves constructing a Cech complex from the nerve of the open cover, with cochains formed by sections over intersections, and the differential defined by alternating sums of restriction maps. This method offers explicit computational techniques that are particularly effective for spaces with good covers, enabling concrete calculations of cohomology groups relevant in algebraic topology and complex geometry.
Deligne Cohomology: Definition and Framework
Deligne cohomology is a hybrid cohomological theory combining differential forms and integral cohomology, providing a refined invariant capturing both topological and geometric information on smooth manifolds. It is defined using a hypercohomology of a complex of sheaves involving smooth differential forms and the sheaf of locally constant functions, thus bridging the gap between de Rham and Cech cohomology. This framework allows Deligne cohomology to classify differential characters, line bundles with connection, and plays a crucial role in arithmetic geometry and index theory.
Key Differences Between Čech and Deligne Cohomology
Cech cohomology captures topological information using open covers and cochains, providing a purely topological invariant of spaces, while Deligne cohomology integrates both topological and differential-geometric data by combining sheaf cohomology with differential forms, thus encoding richer structures like characteristic classes with connections. The key difference lies in Deligne cohomology's ability to refine topological classes by incorporating smooth structures, which makes it essential in studying complex manifolds and gauge theories where curvature and holonomy play roles. Cech cohomology is computationally simpler and more abstract, whereas Deligne cohomology offers a framework suitable for geometric quantization and arithmetic geometry due to its mixed sheaf-theoretic and analytic nature.
Interrelations and Compatibility
Cech cohomology and Deligne cohomology interrelate through their role in classifying geometric and topological structures on complex manifolds, where Cech cohomology provides a computational framework for sheaf cohomology and Deligne cohomology extends this by incorporating differential forms to capture finer geometric data, such as line bundles with connection. Compatibility arises in their shared capacity to represent characteristic classes and mixed Hodge structures, allowing Deligne cohomology to refine Cech cohomological invariants with additional analytic and differential information. This interrelation is fundamental in areas like arithmetic geometry and gauge theory, where Deligne cohomology serves as a bridge linking topological invariants from Cech theory to complex analytic and differential geometric contexts.
Applications in Algebraic Geometry and Topology
Cech cohomology provides a computationally accessible framework for studying the topology of algebraic varieties and complex manifolds by using open covers to analyze sheaf cohomology. Deligne cohomology combines algebraic and differential geometric data, playing a crucial role in the study of arithmetic algebraic geometry, mixed Hodge structures, and the classification of algebraic cycles through intermediate Jacobians. Applications include the characterization of line bundles with connection, regulator maps in K-theory, and refined invariants in both complex geometry and topological quantum field theory.
Examples Illustrating Both Cohomologies
Cech cohomology is often exemplified by computations on simple topological spaces like the circle \(S^1\), where it effectively detects the fundamental group through the first cohomology group \(H^1(S^1,\mathbb{Z}) \cong \mathbb{Z}\). Deligne cohomology extends these examples by incorporating differential form data, illustrated by the classification of line bundles with connection on smooth manifolds, where Deligne's group \(H^2_D(X,\mathbb{Z}(1))\) captures both topological and geometric information. For instance, while Cech cohomology classifies principal bundles topologically, Deligne cohomology refines this to include curvature data, making it essential in gauge theory and complex geometry.
Conclusion: Choosing the Right Cohomological Tool
Cech cohomology offers a combinatorial approach well-suited for computations in topological spaces and classical sheaf theory, while Deligne cohomology integrates differential forms and sheaf cohomology, providing a powerful tool for arithmetic geometry and gauge theory. The choice between these depends on the application: Cech cohomology excels in purely topological contexts, whereas Deligne cohomology is preferred for capturing arithmetic structures and mixed Hodge theoretic information. Researchers must weigh computational simplicity against richer geometric data when selecting the appropriate cohomological framework.
Čech cohomology Infographic
 libterm.com
libterm.com