Jordan measure defines the size of a set in Euclidean space by approximating it with finite unions of rectangles, focusing on boundary behavior and interior coverage. It is foundational in understanding more advanced concepts like Lebesgue measure while highlighting the importance of measurability and compactness. Explore the rest of the article to deepen Your grasp of how Jordan measure applies to various mathematical contexts.
Table of Comparison
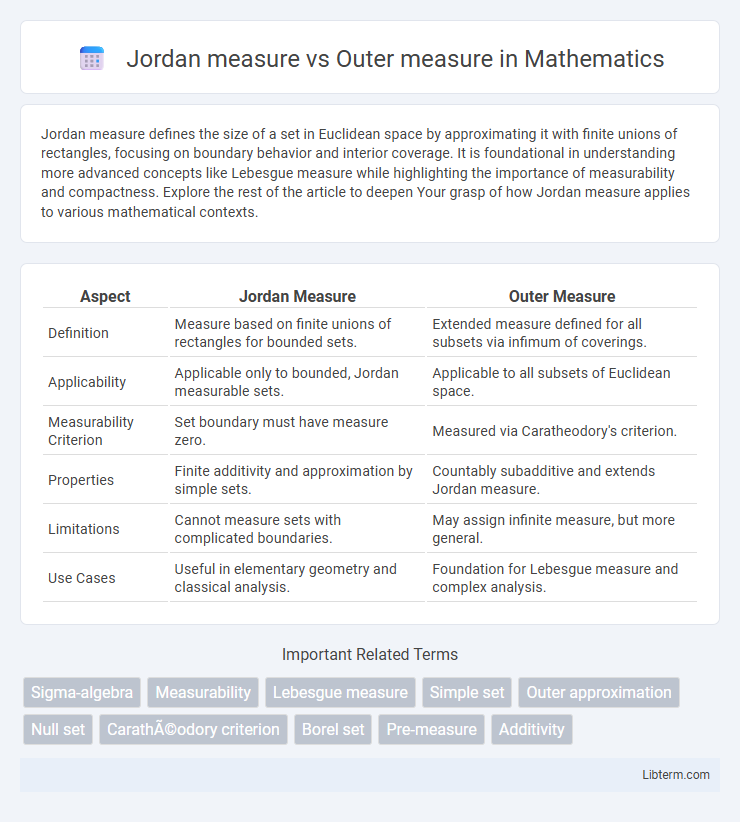
| Aspect | Jordan Measure | Outer Measure |
|---|---|---|
| Definition | Measure based on finite unions of rectangles for bounded sets. | Extended measure defined for all subsets via infimum of coverings. |
| Applicability | Applicable only to bounded, Jordan measurable sets. | Applicable to all subsets of Euclidean space. |
| Measurability Criterion | Set boundary must have measure zero. | Measured via Caratheodory's criterion. |
| Properties | Finite additivity and approximation by simple sets. | Countably subadditive and extends Jordan measure. |
| Limitations | Cannot measure sets with complicated boundaries. | May assign infinite measure, but more general. |
| Use Cases | Useful in elementary geometry and classical analysis. | Foundation for Lebesgue measure and complex analysis. |
Introduction to Jordan Measure and Outer Measure
Jordan measure defines the size of bounded sets in Euclidean spaces using finite unions of rectangles, capturing well-behaved sets with simple boundaries. Outer measure extends this concept by assigning a generalized measure to all subsets through infimum sums of covering rectangles, enabling measurement of more complex or irregular sets. This foundational difference highlights Jordan measure's limitation to measurable sets while outer measure provides a broader framework essential for modern measure theory.
Historical Background and Development
Jordan measure, introduced by Camille Jordan in the late 19th century, was one of the earliest formal attempts to define the measure of sets in Euclidean spaces, relying on the concept of approximating sets with finite unions of intervals or rectangles. Outer measure, developed later by Henri Lebesgue in the early 20th century, extended this idea by considering the infimum of coverages by countably many intervals, laying the foundation for Lebesgue measure and integration. The evolution from Jordan to outer measure marked a significant advancement in measure theory, addressing limitations of Jordan measure regarding sets with intricate boundaries and enabling the rigorous treatment of more complex measurable sets.
Definitions: Jordan Measure vs Outer Measure
Jordan measure defines the size of a bounded set in Euclidean space using finite unions of rectangles, relying on the concept of inner and outer approximations with simple sets. Outer measure extends this idea by assigning a measure to any subset, not limited to well-behaved sets, through the infimum of total volumes of countable coverings by rectangles. While Jordan measure applies to measurable sets with boundaries of measure zero, outer measure provides a more general framework compatible with the Lebesgue measure.
Properties and Axioms of Each Measure
Jordan measure is defined for bounded sets and is finitely additive, satisfying monotonicity and translation invariance but lacks countable additivity, limiting its application to sets with simple boundaries. Outer measure extends to all subsets of a given space, is countably subadditive, monotone, and translation invariant, serving as a precursor to defining measurable sets through Caratheodory's criterion. Unlike Jordan measure, outer measure respects countable subadditivity and provides a foundation for Lebesgue measure, handling more complex and irregular sets beyond simple geometrical shapes.
Differences in Applicability and Scope
Jordan measure applies primarily to bounded, simple sets with well-defined boundaries, making it suitable for sets with finite perimeter and excludes highly irregular or fractal-like shapes. Outer measure extends to all subsets of Euclidean space, including complex and non-measurable sets, offering a broader scope for measuring irregular or infinite sets. The Jordan measure is limited to sets where the boundary has measure zero, whereas outer measure provides a more flexible tool for analyzing arbitrary sets without strict boundary conditions.
Measurable Sets: Criteria and Examples
Jordan measure applies to sets with boundaries of zero area, making them Jordan measurable when their inner and outer Jordan measures coincide, typically involving simple geometric shapes like rectangles and polygons. Outer measure extends to more complex sets by covering them with countable collections of intervals, and a set is Lebesgue measurable if it can be approximated from outside and inside by open and closed sets with arbitrarily small difference in measure. For example, a closed interval is both Jordan and Lebesgue measurable, whereas a set with fractal boundaries may fail Jordan measurability but remain Lebesgue measurable due to the outer measure criteria.
Strengths and Limitations of Jordan Measure
Jordan measure effectively captures the "size" of bounded sets with simple geometric structures, making it suitable for elementary integration problems involving step functions and finite unions of intervals. Its limitation lies in handling more complex or irregular sets since Jordan measure only applies to sets with boundaries of measure zero, failing to measure many fractal or highly disjointed sets. In contrast, outer measure, particularly Lebesgue outer measure, extends beyond these limitations by assigning measure to a broader class of sets, enabling integration over more complicated domains.
Advantages of Outer Measure in Modern Analysis
Outer measure extends Jordan measure by covering a broader class of sets, including those that are not necessarily Jordan measurable, thus providing greater flexibility in modern analysis. It supports countable subadditivity, enabling more robust handling of limit operations and infinite unions that are essential in measure theory and integration. This advantage makes outer measure foundational in developing Lebesgue measure and refining the understanding of measurable functions and sets.
Practical Applications in Real Analysis
Jordan measure is primarily effective for measuring bounded sets with simple boundaries in real analysis, making it suitable for problems involving piecewise constant functions or elementary shapes. Outer measure extends this concept by accommodating more complex or irregular sets through countable coverings, thus supporting broader applications such as Lebesgue integration and measure theory. Practical uses emphasize Jordan measure in classical geometric problems, while outer measure underpins advanced topics like measurable functions and convergence theorems.
Conclusion: Choosing the Appropriate Measure
Jordan measure applies effectively to bounded sets with simple boundaries, offering precise evaluations for well-defined, elementary shapes. Outer measure extends applicability to more complex or unbounded sets, ensuring measurable coverage but potentially lacking exactness in fine detail. Selecting the appropriate measure depends on set complexity and precision needs, with Jordan measure favored for simplicity and outer measure for broader generality in measure theory.
Jordan measure Infographic
 libterm.com
libterm.com