Approximation techniques provide practical solutions when exact values are difficult or impossible to determine, enabling efficient problem-solving in fields like mathematics, computer science, and engineering. These methods balance precision and computational resources, ensuring results are sufficiently close to the true value for real-world applications. Explore the rest of the article to understand how approximation can enhance your analytical skills and decision-making.
Table of Comparison
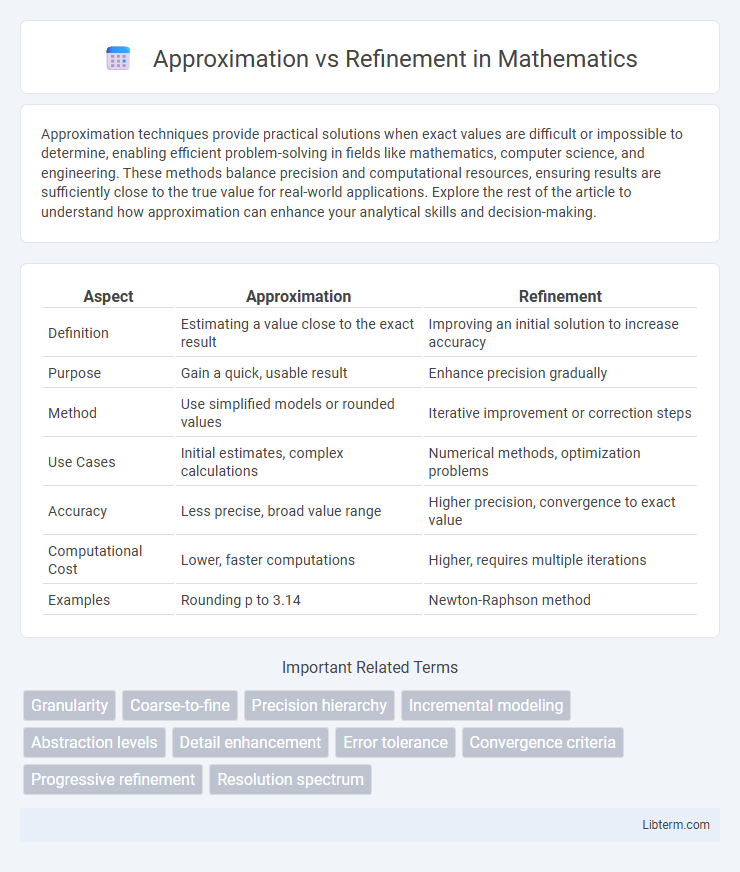
| Aspect | Approximation | Refinement |
|---|---|---|
| Definition | Estimating a value close to the exact result | Improving an initial solution to increase accuracy |
| Purpose | Gain a quick, usable result | Enhance precision gradually |
| Method | Use simplified models or rounded values | Iterative improvement or correction steps |
| Use Cases | Initial estimates, complex calculations | Numerical methods, optimization problems |
| Accuracy | Less precise, broad value range | Higher precision, convergence to exact value |
| Computational Cost | Lower, faster computations | Higher, requires multiple iterations |
| Examples | Rounding p to 3.14 | Newton-Raphson method |
Understanding Approximation and Refinement
Approximation involves creating a simplified model or estimate that captures essential features while ignoring details, facilitating faster decision-making and analysis. Refinement systematically improves this initial approximation by incorporating additional data or constraints, leading to more accurate and reliable results. Understanding the balance between approximation and refinement is crucial for optimizing computational efficiency and solution precision in fields like numerical analysis and machine learning.
Key Differences Between Approximation and Refinement
Approximation involves simplifying complex data or processes to achieve a near value or solution quickly, often sacrificing precision for speed and ease. Refinement focuses on iterative improvement by enhancing accuracy and detail, progressively reducing error margins in the result. Key differences lie in their objectives: approximation prioritizes efficiency and generality, while refinement targets precision and exactness through systematic adjustments.
Historical Background and Evolution
Approximation and refinement techniques have evolved significantly since their early use in classical mathematics, particularly in numerical methods developed by ancient Greek mathematicians such as Archimedes. During the Renaissance, advancements in calculus by Newton and Leibniz introduced more systematic approaches to refining approximations, enabling the precise calculation of limits and derivatives. The digital revolution of the 20th century further propelled these methods, with iterative algorithms and computational models refining approximations to unprecedented levels of accuracy in science and engineering.
Importance of Approximation in Problem Solving
Approximation plays a crucial role in problem solving by enabling quicker solutions when exact answers are computationally infeasible or time-consuming, especially in complex systems like large-scale optimization or machine learning models. It allows for the simplification of problems while maintaining an acceptable level of accuracy, facilitating efficient decision-making and resource allocation. Approximate methods also provide foundational insights that guide subsequent refinement processes, enhancing overall solution quality and robustness.
Role of Refinement in Achieving Precision
Refinement plays a critical role in achieving precision by iteratively improving an initial approximation through systematic adjustments and error minimization. It enhances accuracy by focusing on narrowing the difference between estimated values and exact solutions using methods such as adaptive algorithms or gradient-based optimization. This process ensures the convergence towards highly precise results in complex computational models and numerical analyses.
Applications in Science and Engineering
Approximation methods enable scientists and engineers to model complex systems by simplifying equations, allowing for faster computations and initial design insights. Refinement techniques improve these models iteratively, enhancing accuracy and predictive capability essential for simulations in fluid dynamics, structural analysis, and climate modeling. Combining approximation with refinement balances computational efficiency and precision, driving innovations in aerospace engineering, material science, and computational biology.
Benefits and Limitations of Approximation
Approximation techniques provide faster processing and reduced computational costs by simplifying complex problems, especially useful in large-scale data analysis and real-time systems. However, these methods may sacrifice accuracy and precision, potentially leading to errors or less reliable outcomes in critical applications. Balancing speed and quality is essential, as over-reliance on approximation can compromise decision-making and detailed insights.
When to Use Refinement Over Approximation
Refinement should be used over approximation when high precision and accuracy are critical, such as in engineering design, scientific simulations, and detailed data analysis. In cases where minor errors can lead to significant consequences or when models need to be validated against empirical data, refinement ensures improved reliability and reduces uncertainty. Choosing refinement supports the development of robust solutions by iteratively enhancing detail and reducing error margins crucial for performance optimization.
Real-World Examples Illustrating Both Approaches
Approximation methods are widely used in weather forecasting, where models predict general patterns using simplified equations to deliver timely results despite inherent uncertainties. Refinement techniques appear prominently in engineering design processes, where initial prototypes are iteratively improved through precise measurements and feedback to enhance performance and accuracy. Both approaches balance speed and precision depending on the context, such as approximating traffic flow with statistical models versus refining vehicle designs based on detailed computational simulations.
Choosing the Right Method: Approximation or Refinement
Choosing between approximation and refinement depends on the accuracy requirements and computational resources available. Approximation methods provide quicker results by simplifying complex problems, making them ideal for large datasets or real-time analysis, whereas refinement techniques focus on enhancing precision through iterative improvements and detailed adjustments. Evaluating the trade-offs between speed and accuracy is crucial for selecting the appropriate approach in data modeling, numerical analysis, or machine learning applications.
Approximation Infographic
 libterm.com
libterm.com