A quasimetric is a generalization of a metric space where the distance function may not be symmetric, meaning the distance from point A to B can differ from the distance from B to A. This concept is crucial in various fields such as computer science, particularly in network theory and algorithms, where directional distances affect computations. Explore the rest of this article to understand how quasimetrics influence practical applications and theoretical developments.
Table of Comparison
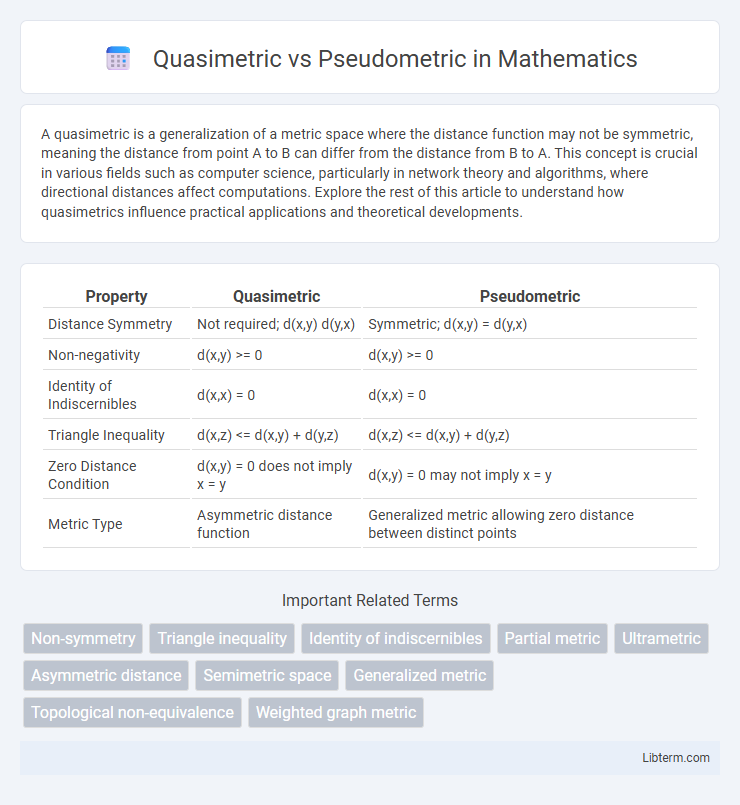
| Property | Quasimetric | Pseudometric |
|---|---|---|
| Distance Symmetry | Not required; d(x,y) d(y,x) | Symmetric; d(x,y) = d(y,x) |
| Non-negativity | d(x,y) >= 0 | d(x,y) >= 0 |
| Identity of Indiscernibles | d(x,x) = 0 | d(x,x) = 0 |
| Triangle Inequality | d(x,z) <= d(x,y) + d(y,z) | d(x,z) <= d(x,y) + d(y,z) |
| Zero Distance Condition | d(x,y) = 0 does not imply x = y | d(x,y) = 0 may not imply x = y |
| Metric Type | Asymmetric distance function | Generalized metric allowing zero distance between distinct points |
Introduction to Quasimetric and Pseudometric Spaces
Quasimetric spaces generalize metric spaces by relaxing the symmetry condition, allowing the distance from point A to B to differ from the distance from B to A, which is crucial in modeling directed networks and asymmetric relations. Pseudometric spaces further generalize metric spaces by permitting distinct points to have zero distance, useful in identifying equivalence classes and analyzing indistinguishable data points. Understanding the foundational differences between quasimetric and pseudometric spaces enables the exploration of more flexible distance functions in topology and applied mathematics.
Defining Quasimetric: Key Properties and Examples
A quasimetric is a generalization of a metric space where the distance function d satisfies non-negativity, identity of indiscernibles (d(x, x) = 0), and the triangle inequality, but it may lack symmetry, meaning d(x, y) is not necessarily equal to d(y, x). Key properties include the relaxation of symmetry, which allows modeling directional or asymmetric relationships commonly found in tasks like network routing and time-dependent travel distances. Examples of quasimetrics include shortest path distances in directed graphs and travel times in traffic networks where reverse paths have different costs.
Understanding Pseudometric: Essential Characteristics
A pseudometric is a distance function on a set that satisfies non-negativity, symmetry, and the triangle inequality but allows distinct points to have zero distance, unlike a metric. This key characteristic differentiates pseudometrics from quasimetrics, where symmetry is generally not required. Understanding pseudometric spaces is crucial in functional analysis and topology, as they enable the study of objects up to indistinguishability defined by zero pseudodistance.
Symmetry vs Asymmetry: Major Differences
Quasimetric spaces lack symmetry, meaning the distance from point A to B may differ from B to A, while pseudometric spaces maintain symmetry with equal distances in both directions. This asymmetry in quasimetric spaces is essential for modeling directed relationships such as traffic flow or web navigation. In contrast, pseudometrics extend metrics by allowing distinct points to have zero distance but preserve symmetry, making them suitable for clustering and similarity tasks.
Triangle Inequality in Quasimetric and Pseudometric
Quasimetric spaces relax symmetry but enforce a modified triangle inequality d(x,z) <= d(x,y) + d(y,z), allowing directional distances, while pseudometric spaces maintain symmetry and satisfy the standard triangle inequality d(x,z) <= d(x,y) + d(y,z) with zero distance between distinct points possible. The triangle inequality in quasimetric spaces reflects non-symmetric measures common in directed graphs and asymmetric cost functions, contrasting with pseudometrics that generalize metrics by permitting zero-length between distinct points yet preserve symmetric distance. Understanding these distinctions in triangle inequality application aids in selecting appropriate mathematical models for asymmetric versus symmetric distance structures in analysis and topology.
Applications of Quasimetrics in Real-World Scenarios
Quasimetric spaces, characterized by their non-symmetric distance functions, find crucial applications in computer science, particularly in network routing where asymmetric costs model variable traffic latency. In robotics and control theory, quasimetrics effectively represent directional constraints and path dependencies, enabling optimized navigation and motion planning. These applications leverage the unique properties of quasimetrics to handle real-world scenarios involving asymmetry and directionality that pseudometrics, which require symmetry, cannot adequately capture.
Role of Pseudometrics in Mathematical Analysis
Pseudometrics play a crucial role in mathematical analysis by allowing the treatment of spaces where distinct points can have zero distance, enabling the study of equivalence classes and quotient spaces. Unlike quasimetric spaces, where the distance function may lack symmetry, pseudometrics ensure symmetry and the relaxed triangle inequality, providing a framework for generalized metric spaces. This flexibility facilitates the analysis of convergence, continuity, and compactness in contexts where strict metric conditions are too restrictive.
Comparative Table: Quasimetric vs Pseudometric
Quasimetric and pseudometric differ primarily in symmetry and the satisfaction of distance properties; quasimetric distances are generally asymmetric, meaning d(x, y) d(y, x) in some cases, while pseudometric distances are symmetric with d(x, y) = d(y, x). A quasimetric does not require the symmetry property but maintains non-negativity and the triangle inequality; a pseudometric allows zero distance between distinct points but enforces symmetry and the triangle inequality. The comparative table highlights these distinctions: symmetry (quasimetric: no, pseudometric: yes), identity of indiscernibles (quasimetric: no, pseudometric: no), and triangle inequality (both: yes).
Choosing the Right Metric for Your Problem
Quasimetric and pseudometric both extend the concept of distance but differ in symmetry and identity conditions, impacting their suitability for various applications. Choose a quasimetric when directionality matters, such as in transportation networks or asymmetrical cost problems, where d(x, y) d(y, x) is meaningful. Opt for a pseudometric when symmetric similarity measures with zero self-distance exceptions are needed, commonly in clustering algorithms or scenarios with indistinguishable points.
Conclusion: Implications and Further Research
Quasimetric and pseudometric spaces differ primarily in symmetry and identity properties, influencing their applications in topology and geometry. Understanding these distinctions enables deeper insights into asymmetric distance measures important in fields like computer science and network theory. Further research could explore the extension of quasimetric properties in complex systems and their impact on optimization algorithms and spatial analysis.
Quasimetric Infographic
 libterm.com
libterm.com