Weight filtration is a mathematical technique used to analyze complex structures by breaking them down into simpler, weighted layers that reveal underlying patterns and relationships. This method is essential in fields like algebraic geometry and topological data analysis, providing insights into the behavior of various mathematical objects. Discover how weight filtration can transform your understanding by exploring the detailed explanations and applications in the rest of this article.
Table of Comparison
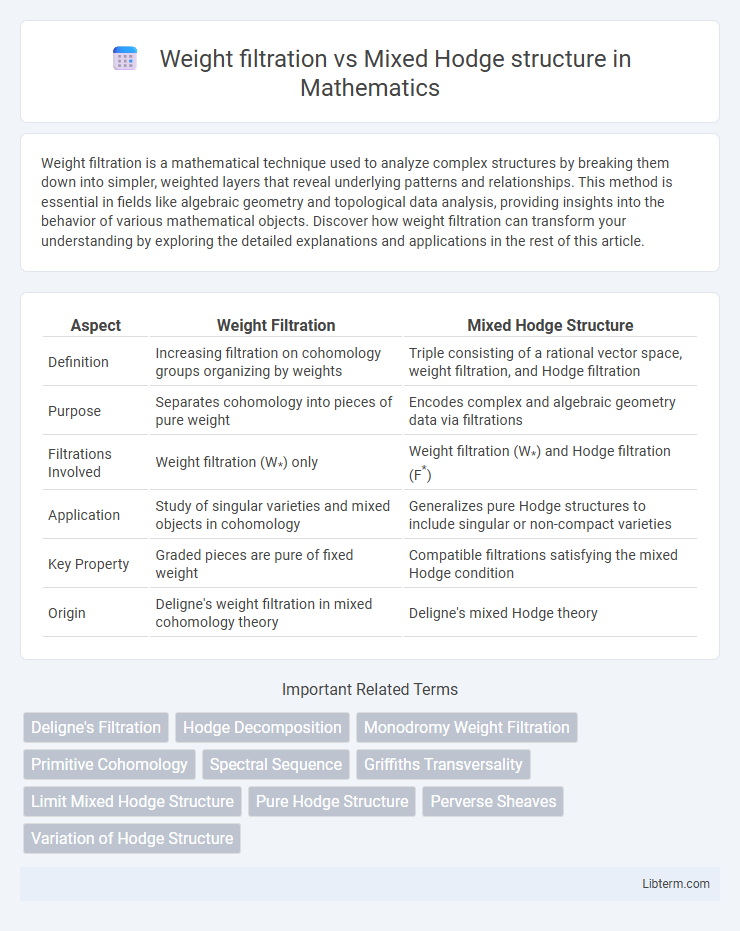
| Aspect | Weight Filtration | Mixed Hodge Structure |
|---|---|---|
| Definition | Increasing filtration on cohomology groups organizing by weights | Triple consisting of a rational vector space, weight filtration, and Hodge filtration |
| Purpose | Separates cohomology into pieces of pure weight | Encodes complex and algebraic geometry data via filtrations |
| Filtrations Involved | Weight filtration (W*) only | Weight filtration (W*) and Hodge filtration (F*) |
| Application | Study of singular varieties and mixed objects in cohomology | Generalizes pure Hodge structures to include singular or non-compact varieties |
| Key Property | Graded pieces are pure of fixed weight | Compatible filtrations satisfying the mixed Hodge condition |
| Origin | Deligne's weight filtration in mixed cohomology theory | Deligne's mixed Hodge theory |
Introduction to Weight Filtration and Mixed Hodge Structure
Weight filtration organizes the cohomology of algebraic varieties into a finite increasing sequence of subspaces that reflect the geometric complexity and singularities of the variety. Mixed Hodge structure enriches the weight filtration by coupling it with a Hodge filtration, encoding both topological and complex-analytic information into a bi-filtered vector space. These structures are fundamental in understanding variations of Hodge structures, especially in the study of degenerations and singular algebraic varieties.
Historical Background and Mathematical Importance
Weight filtration, introduced by Pierre Deligne in the 1970s, serves as a fundamental tool to analyze the cohomology of algebraic varieties through an increasing filtration that captures the complexity of singularities. Mixed Hodge structures, also developed by Deligne, extend the pure Hodge structures by combining weight and Hodge filtrations, providing a richer framework to study singular or non-compact algebraic varieties. These concepts are pivotal in modern algebraic geometry and number theory, enabling deep insights into the topology of complex algebraic varieties and contributing to advances in motives and arithmetic geometry.
Basic Definitions: Weight Filtration
Weight filtration, a fundamental concept in algebraic geometry, is an increasing sequence of subspaces \( \{W_k\} \) of a vector space associated with a cohomology group, reflecting the "weights" or levels of complexity of algebraic cycles. Each step \( W_k \) captures elements of weight less than or equal to \( k \), providing a stratification that reveals the graded pieces essential for constructing mixed Hodge structures. This filtration is crucial in describing the mixed Hodge structure, where it interacts with the Hodge filtration to encode intricate topological and geometric information of complex algebraic varieties.
Overview of Mixed Hodge Structure
Mixed Hodge structures extend the concept of classical Hodge structures by incorporating a weight filtration alongside the Hodge filtration, providing a refined algebraic and geometric framework. This structure enables the study of complex algebraic varieties with singularities or non-compactness by encoding their cohomological properties through a bi-filtered vector space. The interplay between the weight and Hodge filtrations in a mixed Hodge structure facilitates deep insights into the topology and arithmetic of algebraic varieties.
Key Differences between Weight Filtration and Mixed Hodge Structures
Weight filtration is a finite increasing filtration on a cohomology group that reflects the algebraic or geometric complexity of a variety, while mixed Hodge structures combine both weight filtration and Hodge filtration to provide a richer, bi-filtered structure expressing variations of Hodge decompositions. Weight filtration categorizes cohomological elements by their 'weights,' capturing singularities or non-pure features, whereas mixed Hodge structures integrate these weights with complex conjugate gradings to describe intricate relations in cohomology. The essential difference lies in mixed Hodge structures encompassing two filtrations to encode both topological and complex-analytic information, whereas weight filtration offers a singular graded stratification related mainly to the algebraic structure.
Role of Weight Filtration in Algebraic Geometry
Weight filtration plays a crucial role in algebraic geometry by organizing the cohomology groups of algebraic varieties into graded pieces that reflect geometric and topological complexity. It provides a systematic framework for analyzing singularities and degenerations through the construction of mixed Hodge structures, which combine weight and Hodge filtrations to capture both algebraic and analytical information. This filtration enables the decomposition of intricate geometric objects into simpler components, facilitating deeper insights into their arithmetic and geometric properties.
Applications of Mixed Hodge Structures
Mixed Hodge structures provide a powerful framework for analyzing the topology of algebraic varieties by decomposing their cohomology into graded pieces, revealing intricate geometric and arithmetic information. Applications include the study of singularities, variations of Hodge structures in moduli spaces, and arithmetic geometry, where they offer tools for understanding rational points and motives. Weight filtration alone captures pure layers, but mixed Hodge structures extend this by combining weight and Hodge filtrations to handle more complex objects with non-pure cohomology.
Interplay between Weight Filtration and Mixed Hodge Structure
Weight filtration and mixed Hodge structure are deeply intertwined in the study of algebraic varieties, with weight filtration providing a graded decomposition that reflects the complexity of singularities and cohomological behavior. Mixed Hodge structures extend pure Hodge structures by incorporating weight filtration alongside the Hodge filtration, enabling the classification of cohomology groups with mixed weights arising from non-smooth or non-compact varieties. The interplay between weight filtration and mixed Hodge structures facilitates crucial insights into the degeneration of spectral sequences and the behavior of limit mixed Hodge structures in degenerating families of algebraic varieties.
Examples Illustrating Both Concepts
Weight filtration and Mixed Hodge structure can be illustrated using the cohomology of singular algebraic varieties, where weight filtration stratifies cohomology groups by increasing complexity of algebraic cycles. For example, the cohomology of a nodal curve shows a non-trivial weight filtration reflecting the contribution of singular points, while the Mixed Hodge structure captures both the weight filtration and the Hodge filtration revealing the interplay between topology and complex structure. Another instance is the degeneration of a family of smooth projective varieties to a singular fiber, where the weight filtration arises from the monodromy action and the Mixed Hodge structure encodes variations of Hodge structures on the smooth fibers combined with the singular limit behavior.
Future Directions and Open Problems
Future research on weight filtration and mixed Hodge structures aims to deepen the understanding of their interplay in non-classical and singular spaces, expanding beyond smooth projective varieties. Key open problems include characterizing the behavior of weight filtrations under degenerations and analyzing their compatibility with other cohomological invariants in arithmetic geometry. Advances in computational techniques for explicit calculations of mixed Hodge structures will further illuminate their role in mirror symmetry and Hodge theory applications.
Weight filtration Infographic
 libterm.com
libterm.com