The pushforward functor is a fundamental concept in category theory and algebraic geometry that maps sheaves or objects along a continuous or morphic map between spaces. It preserves the structure by associating data from one space to another, often facilitating the study of how local properties transform under mappings. Explore the rest of this article to deepen your understanding of how the pushforward functor operates and its applications in various mathematical contexts.
Table of Comparison
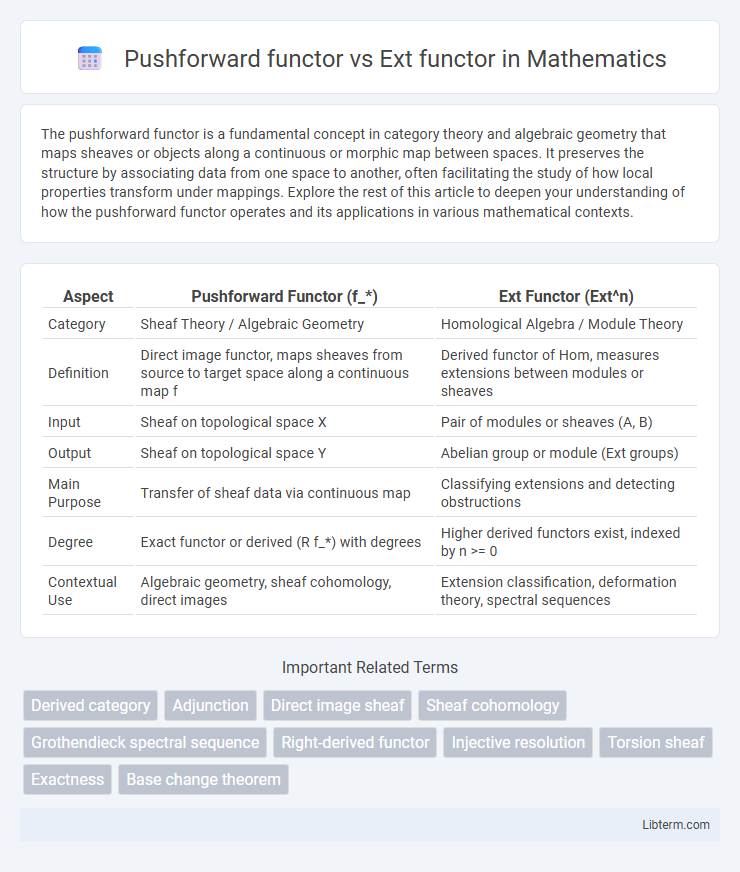
| Aspect | Pushforward Functor (f_*) | Ext Functor (Ext^n) |
|---|---|---|
| Category | Sheaf Theory / Algebraic Geometry | Homological Algebra / Module Theory |
| Definition | Direct image functor, maps sheaves from source to target space along a continuous map f | Derived functor of Hom, measures extensions between modules or sheaves |
| Input | Sheaf on topological space X | Pair of modules or sheaves (A, B) |
| Output | Sheaf on topological space Y | Abelian group or module (Ext groups) |
| Main Purpose | Transfer of sheaf data via continuous map | Classifying extensions and detecting obstructions |
| Degree | Exact functor or derived (R f_*) with degrees | Higher derived functors exist, indexed by n >= 0 |
| Contextual Use | Algebraic geometry, sheaf cohomology, direct images | Extension classification, deformation theory, spectral sequences |
Introduction to Pushforward and Ext Functors
The pushforward functor, denoted as \(f_*\), maps sheaves or modules from the category over a space \(X\) to a category over a space \(Y\) through a continuous map \(f: X \to Y\), preserving the structure while translating data along \(f\). The Ext functor \( \mathrm{Ext}^n_R(-, -) \) arises from homological algebra, measuring extensions and classifying higher derived functors of Hom, encoding extensions of modules over a ring \(R\). Both functors serve fundamental roles in algebraic geometry and homological algebra; the pushforward transports sheaf-theoretic data across spaces while Ext captures intrinsic extension classes and cohomological information of modules or sheaves.
Fundamental Concepts in Category Theory
The pushforward functor, often denoted as \( f_* \), maps sheaves or modules along a continuous or morphism of topological spaces or schemes, preserving the composition of morphisms and reflecting the covariant nature of the associated functor. The Ext functor, \( \mathrm{Ext}^n(-,-) \), arises from the derived functors of Hom and measures extensions and obstructions in abelian categories, capturing higher-dimensional cohomological information. Both functors play crucial roles in homological algebra and category theory, with pushforward functors connecting geometric intuition to algebraic structures while Ext functors analyze extension classes and derived categories.
Definition of the Pushforward Functor
The pushforward functor, denoted as \( f_* \), is defined for a continuous map \( f: X \to Y \) between topological spaces and acts on sheaves of abelian groups on \( X \), producing sheaves on \( Y \) by direct image. It assigns to each sheaf \( \mathcal{F} \) on \( X \) the sheaf \( f_*\mathcal{F} \) on \( Y \), where the sections over an open set \( U \subseteq Y \) are given by \( \mathcal{F}(f^{-1}(U)) \). This contrasts with the Ext functor, which measures extensions of modules or sheaves and operates in derived categories, typically constructed via injective resolutions rather than continuous mappings.
Overview of the Ext Functor
The Ext functor measures extensions between modules and provides a derived functor concept capturing higher-order relationships in homological algebra. It computes the classes of extensions, generalizing Hom by encoding obstructions to splitting exact sequences, thereby revealing deep structural information about modules. In contrast, the pushforward functor is a direct image functor in sheaf theory that transfers sheaves along continuous maps without capturing the extension complexities encoded by Ext.
Comparing Functorial Properties
The pushforward functor, denoted \( f_* \), is right exact and preserves colimits, making it suitable for direct image operations in sheaf theory, while the Ext functor, \( \mathrm{Ext}^n(-,-) \), is a derived functor of Hom that measures extensions and is left derived, capturing higher homological information. Unlike the pushforward functor, which acts on morphisms of sheaves and preserves exactness only on the right, the Ext functor encodes obstructions to lifting morphisms, reflecting derived category structures and long exact sequences in cohomology. Comparing their functorial properties highlights the pushforward's geometric intuition versus Ext's algebraic complexity in homological algebra and sheaf cohomology contexts.
Homological Algebra Contexts
Pushforward functors in homological algebra typically refer to derived functors associated with direct image operations on sheaves or modules, preserving exactness properties under certain conditions. The Ext functor measures extensions and classifies equivalence classes of module extensions, serving as a right derived functor of Hom, capturing higher-order homological information. Pushforward functors and Ext functors interact in derived categories, where pushforwards affect the computation of Ext groups by altering the underlying objects' cohomological dimensions and sheaf structures.
Applications in Algebraic Geometry
The pushforward functor \( f_* \) plays a crucial role in relating coherent sheaves on different schemes, enabling the transfer of geometric and cohomological data along morphisms. The Ext functor \(\mathrm{Ext}^i(-,-)\) measures extensions of sheaves and encodes deformation and obstruction theories essential in moduli problems and complex geometry. In algebraic geometry, these functors intersect in applications such as computing sheaf cohomology on fiber bundles, analyzing derived categories, and studying duality theories that connect direct images with Ext groups.
Use-Cases in Sheaf Theory
The pushforward functor \( f_* \) is essential in sheaf theory for inducing sheaves on the target space by mapping sections along a continuous map \( f: X \to Y \), particularly useful in studying direct images and morphisms of topological spaces. The Ext functor, \( \mathrm{Ext}^i \), measures extensions and classifies obstructions in derived categories of sheaves, playing a crucial role in computing cohomological invariants and analyzing sheaf extensions. Use-cases often combine pushforward to transfer data and Ext to resolve extension problems, especially in algebraic geometry and complex analysis contexts.
Key Differences and Interactions
The pushforward functor, denoted as \(f_*\), primarily acts on sheaves or modules by mapping sections along a continuous or morphic map \(f\), preserving the direct image structure. The Ext functor, \(\mathrm{Ext}^n(-, -)\), computes derived functors capturing extensions and obstructions between modules or sheaves, measuring higher cohomological information. Interaction between \(f_*\) and \(\mathrm{Ext}\) arises in the projection formula and in spectral sequences, where pushforward functors transport Ext groups, linking local and global extension data through derived categories.
Summary and Further Reading
The pushforward functor, often denoted as \( f_* \), maps sheaves from one topological space to another preserving direct images, playing a crucial role in derived categories and cohomological studies. The Ext functor, \( \mathrm{Ext}^n \), generalizes the notion of extensions in abelian categories, measuring the extent to which a module fails to be projective and providing deep insights into homological dimensions. For further reading, explore "Sheaves in Geometry and Logic" by Mac Lane and Moerdijk along with Hartshorne's "Algebraic Geometry" for foundational theory on derived functors and Grothendieck's "Tohoku paper" for categorical background on Ext and pushforward functors.
Pushforward functor Infographic
 libterm.com
libterm.com