Path-connected components are subsets of a topological space where any two points can be joined by a continuous path entirely contained within the subset. Understanding these components helps clarify the structure of spaces in fields like algebraic topology and analysis. Explore the rest of the article to deepen your knowledge of path-connected components and their applications.
Table of Comparison
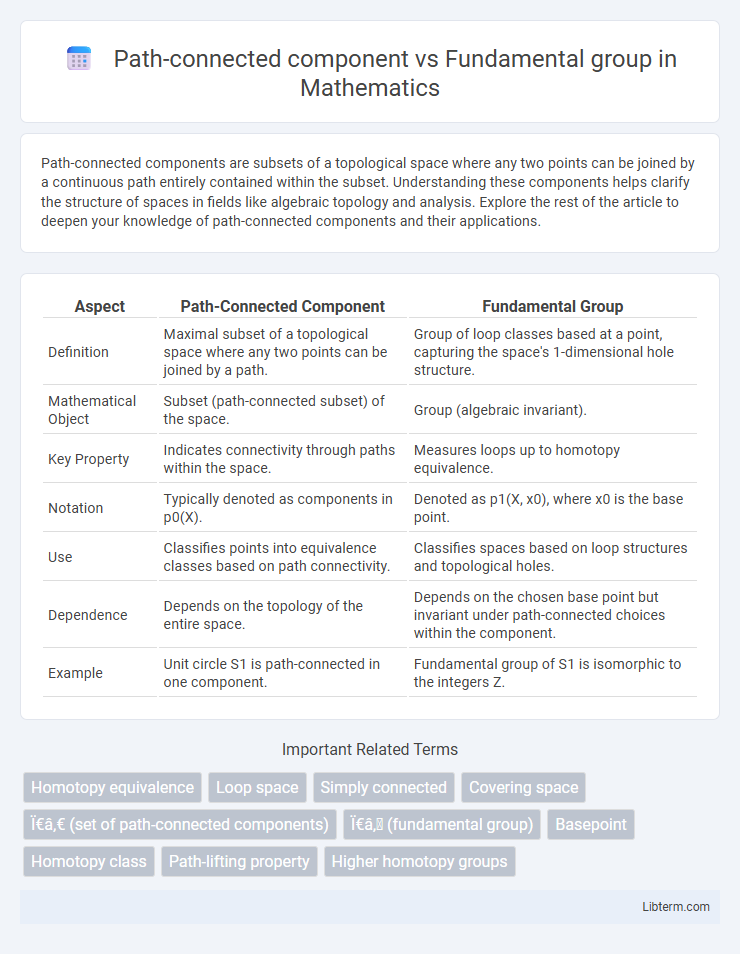
| Aspect | Path-Connected Component | Fundamental Group |
|---|---|---|
| Definition | Maximal subset of a topological space where any two points can be joined by a path. | Group of loop classes based at a point, capturing the space's 1-dimensional hole structure. |
| Mathematical Object | Subset (path-connected subset) of the space. | Group (algebraic invariant). |
| Key Property | Indicates connectivity through paths within the space. | Measures loops up to homotopy equivalence. |
| Notation | Typically denoted as components in p0(X). | Denoted as p1(X, x0), where x0 is the base point. |
| Use | Classifies points into equivalence classes based on path connectivity. | Classifies spaces based on loop structures and topological holes. |
| Dependence | Depends on the topology of the entire space. | Depends on the chosen base point but invariant under path-connected choices within the component. |
| Example | Unit circle S1 is path-connected in one component. | Fundamental group of S1 is isomorphic to the integers Z. |
Introduction to Topological Spaces
Path-connected components partition a topological space into maximal subsets where any two points can be joined by a continuous path, reflecting the space's global connectivity properties. The fundamental group, based at a point in the space, encodes loop structures and path homotopies, providing algebraic invariants that classify topological spaces up to homotopy equivalence. In studying topological spaces, understanding path-connected components is essential for defining the fundamental group, as the latter is only well-defined within a single path-connected component.
Defining Path-Connected Components
A path-connected component of a topological space consists of all points that can be joined to a given point by a continuous path within the space. This concept partitions the space into maximal subsets where every pair of points is path-connected, serving as a fundamental step in understanding the topological structure. The fundamental group captures information about loops based at a point within a path-connected component, classifying these loops up to homotopy and revealing key algebraic invariants of the space.
What is the Fundamental Group?
The fundamental group is a topological invariant that encodes information about the shape and structure of a space by capturing the equivalence classes of loops based at a point, with two loops considered equivalent if one can be continuously deformed into the other. Unlike path-connected components, which classify spaces based on the existence of a continuous path between points, the fundamental group examines the deeper property of loop structures and their homotopy classes, revealing whether holes or obstructions exist within the space. This algebraic structure provides crucial insights for distinguishing spaces that are path-connected but differ in their global topological properties.
Key Differences between Path-Connected Components and Fundamental Group
Path-connected components classify a topological space into distinct subsets where any two points can be joined by a continuous path, emphasizing the space's overall connectivity. The fundamental group, denoted p1, captures the algebraic structure of loops based at a point within a space, revealing deeper information about the space's shape and hole structure through equivalence classes of loops. Key differences lie in their purpose: path-connected components identify connected regions, while the fundamental group analyzes the space's loop structure and topological invariants at a finer, algebraic level.
Examples of Path-Connected Components
Path-connected components partition a topological space into maximal subsets where any two points can be joined by a continuous path, exemplified by the distinct islands in a multi-island archipelago, each forming its own path-connected component. The fundamental group captures the loop structures within a single path-connected component, such as the fundamental group of a circle being isomorphic to the integers, reflecting the number of times a loop winds around. Spaces like the figure-eight have a single path-connected component but a fundamental group that is a free group on two generators, illustrating how these concepts differ in capturing topological properties.
Examples of Fundamental Groups
The fundamental group of a topological space captures its loop structure, distinguishing spaces like the circle \( S^1 \) with fundamental group \(\pi_1(S^1) \cong \mathbb{Z}\), from simply connected spaces such as the disk \( D^2 \) where \(\pi_1(D^2) = \{e\}\). Path-connected components illustrate the largest subsets within which any two points can be joined by a continuous path, but do not reflect the loop-based topological complexity measured by fundamental groups. For example, the wedge sum of two circles \( S^1 \vee S^1 \) has a fundamental group isomorphic to the free group on two generators, revealing richer algebraic information than path-connectedness alone.
Relationship between Path-Connected Components and Fundamental Group
Path-connected components of a topological space categorize points that can be joined by continuous paths, serving as the domain for defining the fundamental group. The fundamental group represents equivalence classes of loops based at a point within a particular path-connected component, capturing the space's loop structures and topological holes. Relationship arises as each path-connected component corresponds to a distinct fundamental group, with path-connectedness ensuring well-defined base points for fundamental group computations.
Significance in Topology: Applications and Insights
Path-connected components partition a topological space into maximal subsets where any two points can be joined by a continuous path, revealing the space's basic connectivity structure. The fundamental group captures the space's essential loop-based properties, detecting holes and obstacles through equivalence classes of loops anchored at a point. Together, these concepts classify spaces by connectivity and shape, enabling applications ranging from algebraic topology in manifold theory to analysis of complex systems and robotics path planning.
Common Misconceptions
Path-connected components represent maximal subsets of a topological space where any two points can be joined by a continuous path, often mistaken as capturing all topological information. The fundamental group, rooted in algebraic topology, encodes information about loops and holes, which cannot be detected purely by path connectivity alone. Confusing these concepts leads to the misconception that a path-connected space must have a trivial fundamental group, ignoring spaces like the circle where the space is path-connected but the fundamental group is nontrivial.
Summary and Further Reading
Path-connected components classify topological spaces into maximal subsets with continuous paths linking any two points, capturing basic connectivity properties. The fundamental group refines this notion by encoding loops based at a point, revealing the space's algebraic structure and higher-order connectivity. For deeper insights, consult "Algebraic Topology" by Allen Hatcher and seminal papers on covering spaces and homotopy theory.
Path-connected component Infographic
 libterm.com
libterm.com