Randomness plays a crucial role in various fields, from computer science algorithms to statistical sampling and cryptography. Understanding the principles behind random processes can enhance Your decision-making and problem-solving skills in unpredictable environments. Explore the rest of this article to uncover how randomness impacts your daily life and technological advancements.
Table of Comparison
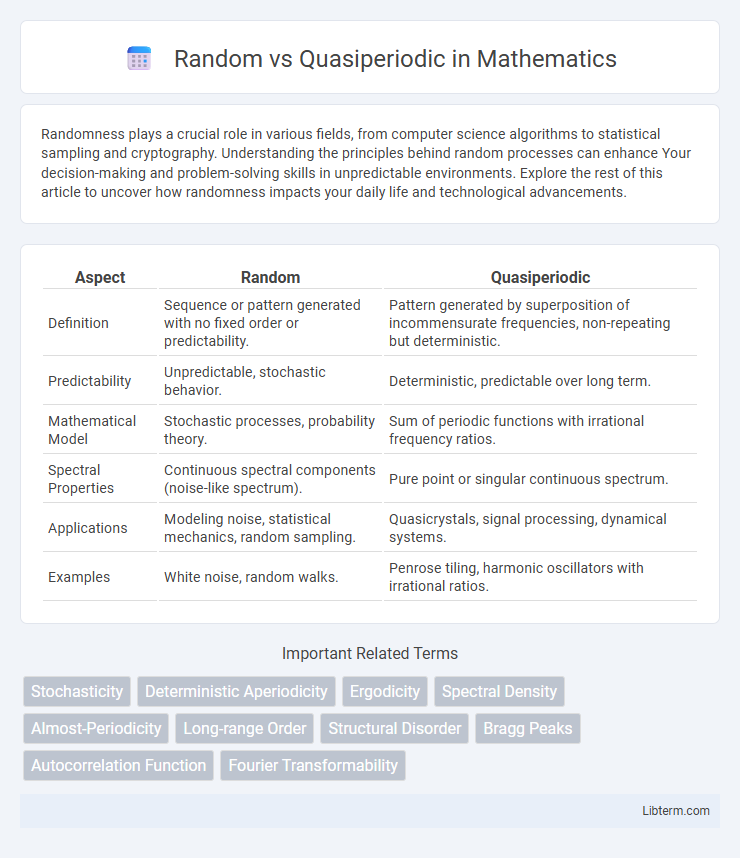
| Aspect | Random | Quasiperiodic |
|---|---|---|
| Definition | Sequence or pattern generated with no fixed order or predictability. | Pattern generated by superposition of incommensurate frequencies, non-repeating but deterministic. |
| Predictability | Unpredictable, stochastic behavior. | Deterministic, predictable over long term. |
| Mathematical Model | Stochastic processes, probability theory. | Sum of periodic functions with irrational frequency ratios. |
| Spectral Properties | Continuous spectral components (noise-like spectrum). | Pure point or singular continuous spectrum. |
| Applications | Modeling noise, statistical mechanics, random sampling. | Quasicrystals, signal processing, dynamical systems. |
| Examples | White noise, random walks. | Penrose tiling, harmonic oscillators with irrational ratios. |
Introduction to Random and Quasiperiodic Systems
Random systems exhibit unpredictable, stochastic behavior characterized by statistical distribution without fixed patterns, playing a crucial role in fields like physics, finance, and biology. Quasiperiodic systems, defined by deterministic yet non-repeating sequences, arise from the superposition of incommensurate frequencies, appearing in areas such as crystallography and dynamical systems. Understanding the fundamental differences between randomness and quasiperiodicity facilitates modeling complex phenomena with varying degrees of order and disorder.
Defining Randomness in Physical and Mathematical Contexts
Randomness in physical contexts refers to unpredictable and inherently uncertain events governed by probabilistic laws, such as quantum fluctuations or thermal noise, where outcomes cannot be precisely determined even with complete information. Mathematically, randomness is characterized by sequences or processes lacking discernible patterns, often modeled by stochastic processes like Brownian motion or random walks, exhibiting statistical properties such as independence and identical distribution. The distinction between random and quasiperiodic systems lies in quasiperiodicity's deterministic nature and structured yet non-repetitive behavior, often describable by incommensurate frequencies in dynamical systems.
Understanding Quasiperiodicity: Concepts and Examples
Quasiperiodicity refers to patterns that exhibit order without exact repetition, distinguishing them from purely random or strictly periodic sequences. Examples include quasicrystals in materials science, where atomic arrangements show non-repeating yet highly ordered structures, and certain mathematical sequences like the Fibonacci series that display quasiperiodic behavior. Understanding quasiperiodicity helps in modeling complex systems that neither fit random randomness nor perfect periodicity, bridging gaps in physics, biology, and signal processing.
Mathematical Distinction: Random vs Quasiperiodic Patterns
Random patterns exhibit unpredictability and lack any deterministic order, characterized by statistical properties such as white noise and stochastic processes. Quasiperiodic patterns show deterministic, non-repeating structures defined by incommensurate frequencies resulting in a spectrum composed of discrete peaks rather than continuous noise. Mathematically, random sequences are modeled by probabilistic distributions with no memory, whereas quasiperiodic functions derive from sums of sinusoidal components with irrational frequency ratios, generating complex but deterministic trajectories.
Applications of Random Structures in Science and Technology
Random structures play a crucial role in modeling complex systems across various scientific fields, including material science, where they describe disordered media such as amorphous solids and porous materials. They enable accurate simulations of phenomena in statistical physics, telecommunications, and cryptography by representing stochastic processes and noise components. Applications extend to biological systems as well, supporting the analysis of genetic variations and neural network behaviors through probabilistic frameworks.
Applications of Quasiperiodic Structures: From Nature to Nanotechnology
Quasiperiodic structures exhibit unique ordering patterns that differ from purely random or strictly periodic arrangements, enabling exceptional material properties such as enhanced thermal insulation and unusual optical behaviors. Applications in nature include the microstructure of certain butterfly wings and plant surfaces, which manipulate light for camouflage or signaling. In nanotechnology, quasiperiodic designs optimize photonic crystals, improve quasicrystal coatings for wear resistance, and facilitate the development of novel electronic devices with tailored conductivity.
Spectral Properties: Comparing Random and Quasiperiodic Systems
Random systems exhibit continuous spectra characterized by broad, noisy frequency distributions due to their lack of inherent order. Quasiperiodic systems display pure point or singular continuous spectra, reflecting their deterministic but non-periodic structure with sharp spectral lines or fractal-like patterns. These distinct spectral properties influence wave propagation, localization phenomena, and physical responses in materials governed by random versus quasiperiodic order.
Detection and Analysis Methods
Detection and analysis methods for random and quasiperiodic signals often involve spectral analysis, autocorrelation functions, and time-frequency decomposition techniques such as wavelet transforms. Random signals typically exhibit broadband spectra and rapidly decaying autocorrelation, while quasiperiodic signals show distinct frequency peaks and persistent autocorrelation patterns. Advanced methods like recurrence quantification analysis and phase space reconstruction enable precise differentiation by capturing underlying dynamical structures and temporal evolutions.
Advantages and Limitations of Random and Quasiperiodic Approaches
Random approaches offer simplicity and robustness in modeling complex, unpredictable systems but can suffer from lack of reproducibility and difficulty in pattern detection. Quasiperiodic methods provide greater predictability and structure, enabling clearer identification of underlying dynamics, though they may struggle with irregularities and noise inherent in real-world data. Both approaches require careful consideration of context-specific goals to balance flexibility and accuracy in analysis and forecasting.
Future Perspectives and Open Questions
Future perspectives in the study of random versus quasiperiodic systems emphasize advancements in characterizing transport properties and phase transitions using machine learning and quantum simulation techniques. Open questions remain about the universality classes governing many-body localization in quasiperiodic potentials and the scalability of computational methods to large system sizes. Enhanced experimental platforms such as ultracold atoms and photonic lattices promise deeper insights into the interplay between disorder and deterministic aperiodicity.
Random Infographic
 libterm.com
libterm.com