The cross product is a fundamental operation in vector mathematics that produces a vector perpendicular to two given vectors in three-dimensional space. It is widely used in physics, engineering, and computer graphics to determine torque, rotational force, and surface normals. Dive deeper into this article to explore the properties, applications, and calculation methods of the cross product.
Table of Comparison
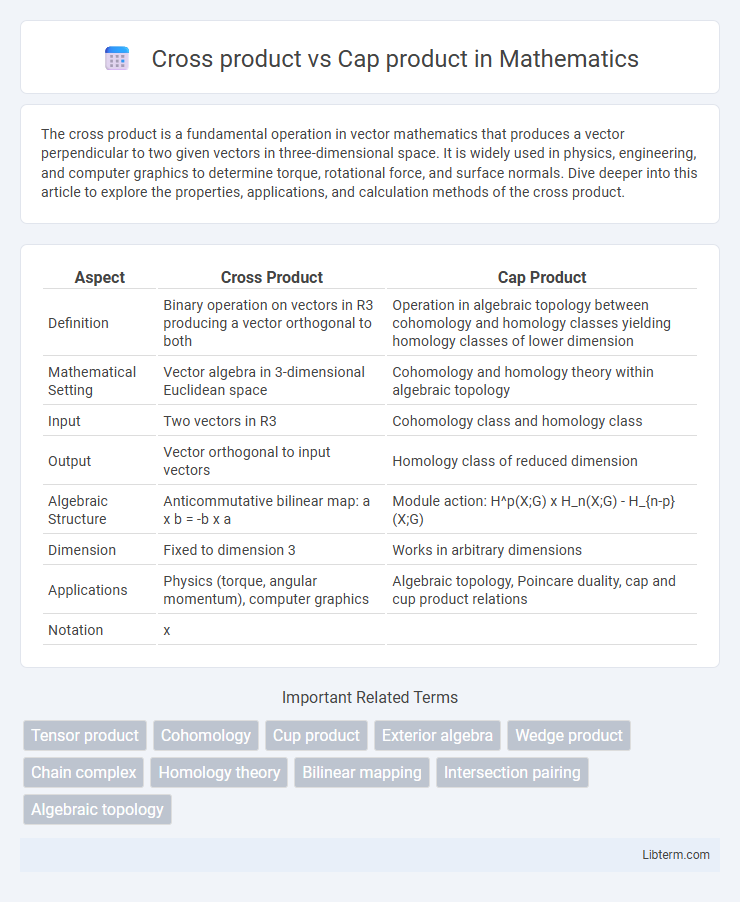
| Aspect | Cross Product | Cap Product |
|---|---|---|
| Definition | Binary operation on vectors in R3 producing a vector orthogonal to both | Operation in algebraic topology between cohomology and homology classes yielding homology classes of lower dimension |
| Mathematical Setting | Vector algebra in 3-dimensional Euclidean space | Cohomology and homology theory within algebraic topology |
| Input | Two vectors in R3 | Cohomology class and homology class |
| Output | Vector orthogonal to input vectors | Homology class of reduced dimension |
| Algebraic Structure | Anticommutative bilinear map: a x b = -b x a | Module action: H^p(X;G) x H_n(X;G) - H_{n-p}(X;G) |
| Dimension | Fixed to dimension 3 | Works in arbitrary dimensions |
| Applications | Physics (torque, angular momentum), computer graphics | Algebraic topology, Poincare duality, cap and cup product relations |
| Notation | x |
Introduction to Cross Product and Cap Product
The cross product is a binary operation on vectors in three-dimensional space that produces a vector perpendicular to both original vectors, commonly used in physics and engineering to determine torque and area. The cap product is an operation in algebraic topology that combines cohomology and homology classes, enabling the evaluation of cohomology classes on homology cycles to produce lower-dimensional homology classes. Understanding these products is essential for applications in vector calculus and topological invariants respectively, highlighting their distinct roles in different mathematical fields.
Definitions and Mathematical Foundations
The cross product is a binary operation on two vectors in three-dimensional space producing a vector orthogonal to both, defined by the determinant of a matrix composed of unit vectors and the components of the two vectors. The cap product, used in algebraic topology, combines cohomology and homology classes to yield a homology class, defined through the action of cochains on chains in a topological space. While the cross product relies on vector algebra and geometric interpretation, the cap product is rooted in algebraic structures on chain complexes, involving homological and cohomological algebra.
Geometric Interpretation of the Cross Product
The geometric interpretation of the cross product emphasizes its role in producing a vector orthogonal to the plane defined by two input vectors, with magnitude equal to the area of the parallelogram they span. This operation contrasts with the cap product, which combines cohomology and homology classes in algebraic topology instead of yielding a spatial vector. The cross product's direction follows the right-hand rule, providing essential applications in physics and engineering related to torque and rotational forces.
Topological Significance of the Cap Product
The cap product in algebraic topology provides a powerful tool for relating homology and cohomology, enabling the extraction of geometric information from cohomological classes by "capping" them with homology cycles. Unlike the cross product, which combines classes from separate spaces into a product space, the cap product acts within a single space to produce homology classes of lower dimension, directly reflecting geometric intersections and duality phenomena such as Poincare duality. This operation plays a crucial role in understanding manifold structures, orientation, and the interaction between cycles and cocycles in a topological space.
Algebraic Properties: Comparison Table
The cross product is a binary operation on vectors in three-dimensional space producing a vector orthogonal to both, characterized by anti-commutativity and distributivity over addition. The cap product operates between cohomology and homology classes in algebraic topology, resulting in a lower-dimensional homology class, exhibiting bilinearity and naturality under continuous maps. While the cross product pertains to vector algebra with geometric interpretations, the cap product serves as an algebraic tool connecting cohomology and homology theories, reflecting topological invariants.
Applications in Physics and Engineering
The cross product is essential in physics and engineering for calculating torque, angular momentum, and electromagnetic force, providing a vector perpendicular to the plane of two input vectors. The cap product, used primarily in algebraic topology, finds applications in theoretical physics, such as in the study of manifolds and field theories, where it relates cohomology and homology classes. Engineers leveraging differential geometry utilize the cap product to analyze complex structural and material properties within multidimensional spaces.
Role in Differential Geometry and Topology
The cross product in differential geometry provides a vector perpendicular to two given vectors in three-dimensional space, essential for defining orientation and normal vectors on surfaces. The cap product, fundamental in algebraic topology, links cohomology and homology groups, enabling the pairing of cochains and chains to produce lower-dimensional homology classes. These operations support the study of manifold structure, with the cross product aiding geometric constructions and the cap product facilitating algebraic invariants in topological spaces.
Computational Methods and Examples
The cross product computes a vector orthogonal to two input vectors in three-dimensional space, commonly used in computer graphics and physics simulations for torque and rotation calculations. The cap product, defined in algebraic topology, combines cohomology and homology classes, essential for computational methods in persistent homology and topological data analysis (TDA). Algorithms for the cross product often involve determinant calculations, while cap product computations rely on chain-cochain pairings implemented in software like Kenzo or Perseus for extracting topological features from data sets.
Common Misconceptions and Pitfalls
The cross product and cap product are often confused due to their similar names, but they operate in different mathematical contexts: the cross product acts on vectors in three-dimensional Euclidean space producing another vector, while the cap product involves cohomology and homology classes in algebraic topology to yield a homology class. A common misconception is treating the cap product as a purely vectorial operation like the cross product, ignoring its role in relating cohomological and homological degrees. Pitfalls include misapplying properties of one product to the other, such as expecting the anticommutativity of the cross product or geometric interpretation like orientation, which do not translate to the algebraic and topological framework of the cap product.
Summary: Choosing Between Cross Product and Cap Product
The cross product generates a vector perpendicular to two input vectors in three-dimensional space, widely used in physics and engineering to find torque or rotational direction. The cap product combines a chain and a cochain in algebraic topology, yielding a lower-dimensional chain, essential for computations in homology and cohomology theories. Choose the cross product for spatial vector analysis and physical applications, and the cap product for algebraic topology problems involving chain and cochain interactions.
Cross product Infographic
 libterm.com
libterm.com