An almost complex structure on a smooth manifold is a geometric structure that equips each tangent space with a linear operator squaring to minus the identity, closely resembling complex multiplication. This framework provides the foundation for studying complex manifolds and plays a crucial role in differential geometry and theoretical physics. Explore the rest of the article to deepen your understanding of how almost complex structures influence manifold theory and complex geometry.
Table of Comparison
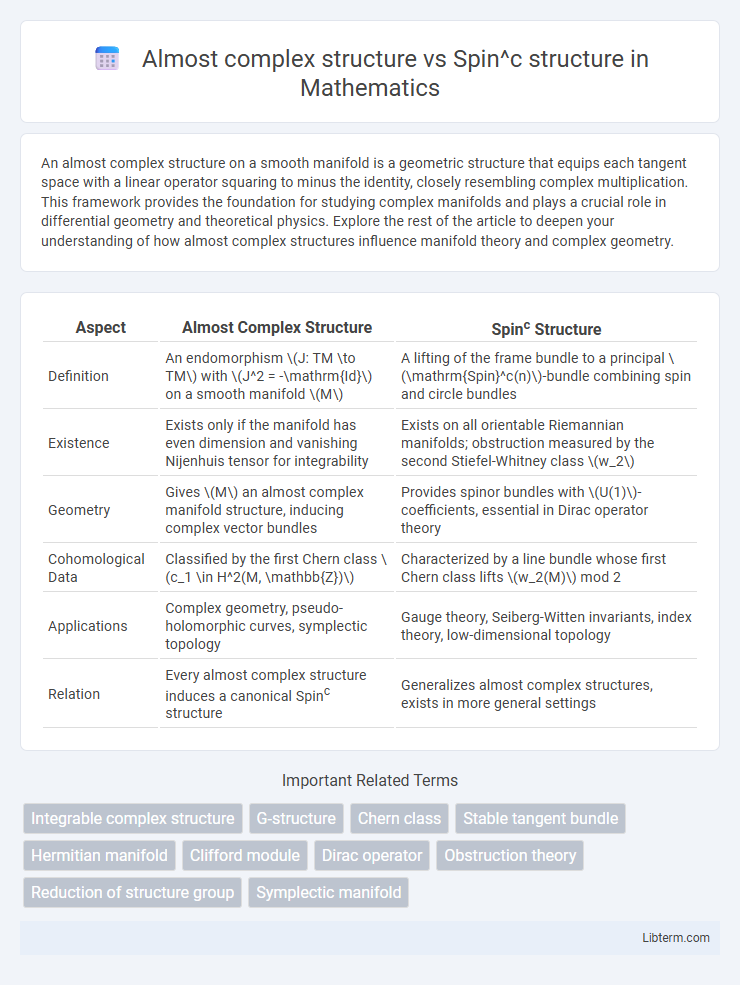
| Aspect | Almost Complex Structure | Spinc Structure |
|---|---|---|
| Definition | An endomorphism \(J: TM \to TM\) with \(J^2 = -\mathrm{Id}\) on a smooth manifold \(M\) | A lifting of the frame bundle to a principal \(\mathrm{Spin}^c(n)\)-bundle combining spin and circle bundles |
| Existence | Exists only if the manifold has even dimension and vanishing Nijenhuis tensor for integrability | Exists on all orientable Riemannian manifolds; obstruction measured by the second Stiefel-Whitney class \(w_2\) |
| Geometry | Gives \(M\) an almost complex manifold structure, inducing complex vector bundles | Provides spinor bundles with \(U(1)\)-coefficients, essential in Dirac operator theory |
| Cohomological Data | Classified by the first Chern class \(c_1 \in H^2(M, \mathbb{Z})\) | Characterized by a line bundle whose first Chern class lifts \(w_2(M)\) mod 2 |
| Applications | Complex geometry, pseudo-holomorphic curves, symplectic topology | Gauge theory, Seiberg-Witten invariants, index theory, low-dimensional topology |
| Relation | Every almost complex structure induces a canonical Spinc structure | Generalizes almost complex structures, exists in more general settings |
Introduction to Almost Complex and Spin^c Structures
An almost complex structure on a smooth manifold is a tensor field that defines a linear complex structure on each tangent space, allowing the manifold to resemble a complex manifold locally without requiring integrability. A Spin^c structure generalizes spin structures by incorporating an additional U(1)-bundle, enabling the definition of spinor bundles on manifolds that may not admit spin structures. Understanding the interplay between almost complex and Spin^c structures is crucial for analyzing topological conditions, such as the existence of Dirac operators and Seiberg-Witten invariants, in differential geometry and mathematical physics.
Definitions: Almost Complex Structure
An almost complex structure on a smooth manifold is a tensor field J of type (1,1) satisfying J2 = -Id, providing each tangent space with a complex vector space structure. This structure generalizes complex manifolds by enabling complex linear algebra over real manifolds without integrability conditions. In contrast, a Spin^c structure extends spin geometry by incorporating a U(1)-bundle, crucial for defining Dirac operators on manifolds that do not admit spin structures.
Definitions: Spin^c Structure
A Spin^c structure on a smooth manifold is a lifting of the frame bundle's SO(n)-principal bundle to a Spin^c(n)-principal bundle, combining Spin and U(1) structures. This construction extends the notion of spin structures by incorporating a complex line bundle, enabling the definition of Dirac operators in broader contexts. Unlike almost complex structures, which define a complex structure on the tangent bundle, Spin^c structures provide topological and geometric frameworks essential for index theory and Seiberg-Witten invariants.
Mathematical Foundations and Preliminaries
An almost complex structure on a smooth manifold is defined by an endomorphism of the tangent bundle squaring to minus the identity, providing the manifold with a complex-linear tangent space structure, which facilitates the study of complex manifolds and holomorphic curves. A Spin^c structure generalizes spin structures by incorporating a principal U(1)-bundle extension, crucial for defining Dirac operators and index theory on manifolds that may not admit spin structures. Understanding the relationship between almost complex structures and Spin^c structures involves analyzing characteristic classes like the first Chern class and second Stiefel-Whitney class, as well as their roles in defining topological obstructions and enabling the construction of Seiberg-Witten invariants.
Existence Conditions on Manifolds
An almost complex structure on a 2n-dimensional manifold requires the tangent bundle to admit an endomorphism J with J2 = -Id, which implies the manifold is orientable and its second Stiefel-Whitney class w2 vanishes mod 2 when lifted to integral cohomology. A Spin^c structure exists on orientable manifolds with a lifting of the frame bundle to a Spin^c group, demanding the vanishing of the third integral Stiefel-Whitney class W3 = b(w2), where b is the Bockstein homomorphism, thus generalizing Spin structures. While every almost complex manifold naturally carries a canonical Spin^c structure, the converse is false, indicating Spin^c existence is a weaker topological condition than admitting an almost complex structure.
Relationship Between Almost Complex and Spin^c Structures
Almost complex structures on a smooth manifold naturally induce Spin^c structures by providing a reduction of the frame bundle to the unitary group U(n), which lifts to the Spin^c group via the canonical determinant line bundle. Every almost complex manifold admits a canonical Spin^c structure determined by its complex structure, and this correspondence is central in defining Dirac operators and studying index theory on complex manifolds. The topological obstruction to the existence of almost complex structures is stronger than that for Spin^c structures, making Spin^c structures more general and applicable in contexts where almost complex structures do not exist.
Examples of Manifolds with Almost Complex Structures
Complex projective spaces CP^n are classical examples of manifolds admitting almost complex structures, arising from their natural complex coordinate charts. Six-dimensional spheres S^6 have an almost complex structure induced by the exceptional Lie group G_2, though they fail to admit a complex structure. Compact complex manifolds such as complex tori and Kahler manifolds inherently possess almost complex structures derived from their complex coordinate systems.
Examples of Manifolds with Spin^c Structures
Many complex manifolds naturally admit Spin^c structures due to their almost complex structures, as seen in complex projective spaces like \(\mathbb{CP}^n\). While every almost complex manifold has a canonical Spin^c structure derived from its complex tangent bundle, Spin^c manifolds also include non-complex examples such as oriented 4-manifolds and certain 3-manifolds. The presence of a Spin^c structure often facilitates the application of Seiberg-Witten invariants in 4-dimensional topology, highlighting the broader geometric significance beyond almost complex cases.
Applications in Geometry and Topology
Almost complex structures enable the definition of holomorphic coordinates on smooth manifolds, facilitating the study of complex manifolds and symplectic topology. Spin^c structures generalize spin structures by incorporating a U(1) bundle twist, crucial for defining Dirac operators in four-manifold topology and Seiberg-Witten invariants. Both structures interplay in gauge theory and index theory, with Spin^c structures providing a broader framework for manifolds lacking almost complex structures, enhancing applications in low-dimensional topology and geometric analysis.
Summary and Comparative Analysis
Almost complex structures define a geometric framework on even-dimensional manifolds by equipping the tangent bundle with a complex structure, enabling the use of complex differential geometry tools. Spin^c structures extend spin structures by incorporating an additional U(1) bundle, allowing for Dirac operator definitions on manifolds that lack spin structures but admit spin^c structures. The key difference lies in their topological obstructions: almost complex structures require an integrable complex structure on the tangent bundle, whereas spin^c structures depend on the second Stiefel-Whitney class lifting to integral cohomology, broadening applicability in index theory and gauge theory.
Almost complex structure Infographic
 libterm.com
libterm.com