The Arzela-Ascoli Theorem characterizes the compact subsets in the space of continuous functions, providing necessary and sufficient conditions based on equicontinuity and uniform boundedness. This theorem is a fundamental tool in functional analysis and has applications in differential equations and approximation theory. Explore the rest of the article to deepen your understanding of how this theorem can be applied in various mathematical contexts.
Table of Comparison
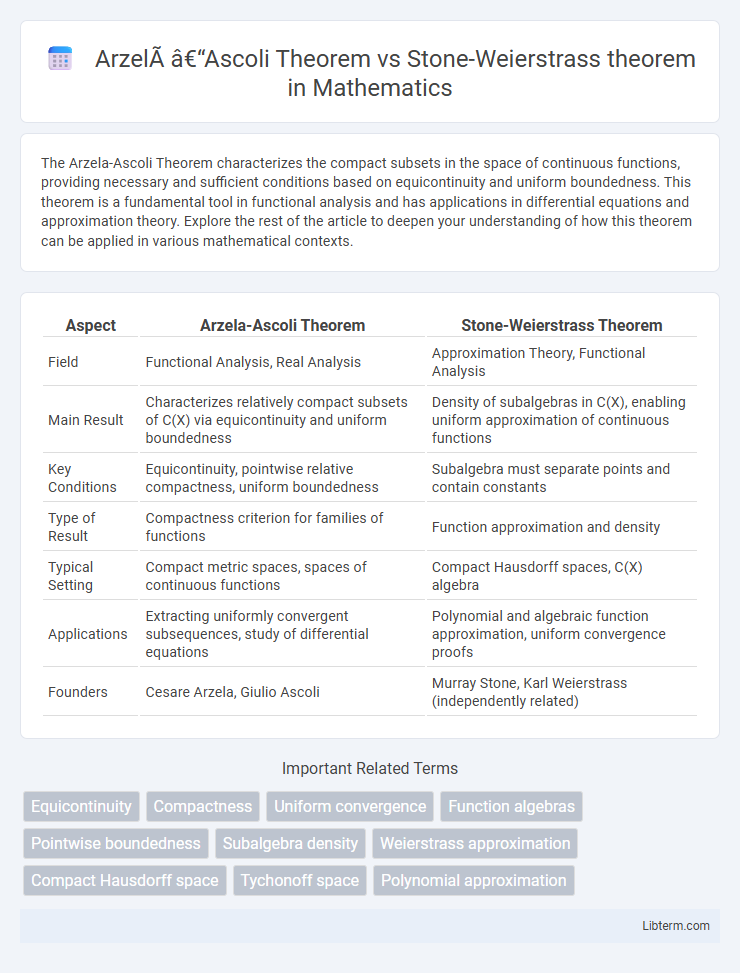
| Aspect | Arzela-Ascoli Theorem | Stone-Weierstrass Theorem |
|---|---|---|
| Field | Functional Analysis, Real Analysis | Approximation Theory, Functional Analysis |
| Main Result | Characterizes relatively compact subsets of C(X) via equicontinuity and uniform boundedness | Density of subalgebras in C(X), enabling uniform approximation of continuous functions |
| Key Conditions | Equicontinuity, pointwise relative compactness, uniform boundedness | Subalgebra must separate points and contain constants |
| Type of Result | Compactness criterion for families of functions | Function approximation and density |
| Typical Setting | Compact metric spaces, spaces of continuous functions | Compact Hausdorff spaces, C(X) algebra |
| Applications | Extracting uniformly convergent subsequences, study of differential equations | Polynomial and algebraic function approximation, uniform convergence proofs |
| Founders | Cesare Arzela, Giulio Ascoli | Murray Stone, Karl Weierstrass (independently related) |
Introduction to Functional Analysis Theorems
The Arzela-Ascoli Theorem characterizes compact subsets of the space of continuous functions by equicontinuity and uniform boundedness, essential for understanding convergence in function spaces. The Stone-Weierstrass Theorem guarantees the density of subalgebras of continuous functions in the uniform norm, enabling function approximation on compact spaces. Both theorems foundationally contribute to Functional Analysis by addressing compactness and approximation in spaces of continuous functions.
Overview of the Arzelà–Ascoli Theorem
The Arzela-Ascoli Theorem characterizes the compactness of a family of real-valued continuous functions on a compact metric space by establishing that any sequence of equicontinuous, uniformly bounded functions contains a uniformly convergent subsequence. This theorem serves as a foundational result in functional analysis and is widely applied in differential equations and approximation theory to ensure the existence of convergent subsequences in function spaces. Unlike the Stone-Weierstrass theorem, which focuses on the density of certain subalgebras in the space of continuous functions, Arzela-Ascoli provides criteria for relative compactness in function spaces, playing a critical role in the study of convergence and continuity properties.
Overview of the Stone-Weierstrass Theorem
The Stone-Weierstrass theorem generalizes the Weierstrass approximation theorem by stating that any subalgebra of C(X), the space of continuous real-valued functions on a compact Hausdorff space X, that separates points and contains the constant functions is dense in C(X) with the uniform norm. This theorem provides a powerful tool for approximating continuous functions by simpler algebraic structures such as polynomials or trigonometric polynomials, enabling extensive applications in analysis and topology. Unlike the Arzela-Ascoli theorem which characterizes compact sets of functions via equicontinuity and pointwise boundedness, the Stone-Weierstrass theorem focuses on the density of function algebras and approximation capabilities.
Core Assumptions and Preconditions
The Arzela-Ascoli theorem requires a family of functions defined on a compact space that is uniformly bounded and equicontinuous, ensuring the existence of a uniformly convergent subsequence. The Stone-Weierstrass theorem demands that the algebra of functions is subalgebra of C(X), contains the constant functions, and separates points on a compact Hausdorff space, allowing uniform approximation of continuous functions by polynomial-like elements. Both theorems fundamentally rely on compactness of the domain but differ in that Arzela-Ascoli focuses on functional sequence properties, while Stone-Weierstrass emphasizes algebraic structure and point separation.
Compactness vs Approximation: Key Differences
The Arzela-Ascoli theorem characterizes compact sets in the space of continuous functions by emphasizing equicontinuity and uniform boundedness as criteria for compactness in function spaces. In contrast, the Stone-Weierstrass theorem focuses on the approximation of continuous functions on compact spaces, asserting that any continuous function can be uniformly approximated by a subalgebra of functions that separates points and contains the constant functions. While Arzela-Ascoli provides conditions for compactness in C(X), Stone-Weierstrass guarantees density of certain function classes in C(X) for uniform approximation.
Applicability in Continuous Function Spaces
The Arzela-Ascoli theorem provides criteria for the compactness of sets of continuous functions based on uniform boundedness and equicontinuity, making it essential for analyzing convergence in function spaces C(X) with X compact. In contrast, the Stone-Weierstrass theorem guarantees that any algebra of functions separating points and containing constants is dense in C(X), enabling polynomial or algebraic approximation of continuous functions. While Arzela-Ascoli is crucial for studying function sequence limits, Stone-Weierstrass focuses on the approximation capabilities within continuous function spaces.
Role in Uniform Convergence
The Arzela-Ascoli Theorem characterizes the precompact subsets of continuous functions on a compact space by providing criteria for uniform convergence through equicontinuity and pointwise boundedness. The Stone-Weierstrass Theorem ensures that any continuous function on a compact space can be uniformly approximated by algebraic subalgebras of functions, typically polynomials or trigonometric functions. Together, these theorems establish foundational frameworks for achieving uniform convergence: Arzela-Ascoli guarantees when subsequences converge uniformly, while Stone-Weierstrass guarantees the density of approximating functions in the uniform norm.
Implications for Banach and Metric Spaces
The Arzela-Ascoli Theorem characterizes the compact subsets of the space of continuous functions on a compact metric space, providing criteria of equicontinuity and uniform boundedness crucial for compactness in Banach spaces like \( C(K) \). The Stone-Weierstrass Theorem guarantees that any subalgebra of \( C(K) \) that separates points and contains the constant functions is dense, implying powerful approximation properties that ensure the ability to approximate any continuous function arbitrarily well. Together, these theorems underpin fundamental structural and approximation results in Banach spaces, enabling convergence analysis and functional approximations within metric spaces.
Practical Examples and Applications
The Arzela-Ascoli theorem is crucial in functional analysis for identifying compact subsets of continuous function spaces, often applied in solving differential equations and proving the convergence of function sequences in numerical analysis. The Stone-Weierstrass theorem underpins approximation theory by guaranteeing that any continuous function on a compact space can be uniformly approximated by polynomial or trigonometric functions, with practical applications in signal processing and machine learning. Together, these theorems enable the development of algorithms for function approximation, optimization, and modeling in engineering and data science.
Summary: Choosing the Appropriate Theorem
The Arzela-Ascoli Theorem is essential for compactness criteria in spaces of continuous functions, particularly when dealing with uniform convergence on compact sets. The Stone-Weierstrass Theorem provides a powerful tool for approximating continuous functions uniformly by polynomials or other subalgebras, ideal for constructive approximation tasks. Selecting between these theorems depends on whether the focus is on function sequence compactness and equicontinuity (Arzela-Ascoli) or on dense approximation within function algebras (Stone-Weierstrass).
Arzelà–Ascoli Theorem Infographic
 libterm.com
libterm.com