Infinite possibilities exist in technology, art, and nature, pushing the boundaries of creativity and innovation beyond limits. Exploring the concept of infinity unlocks new ways of thinking about time, space, and the universe's complexity. Dive into the rest of this article to discover how infinite concepts shape your understanding of the world.
Table of Comparison
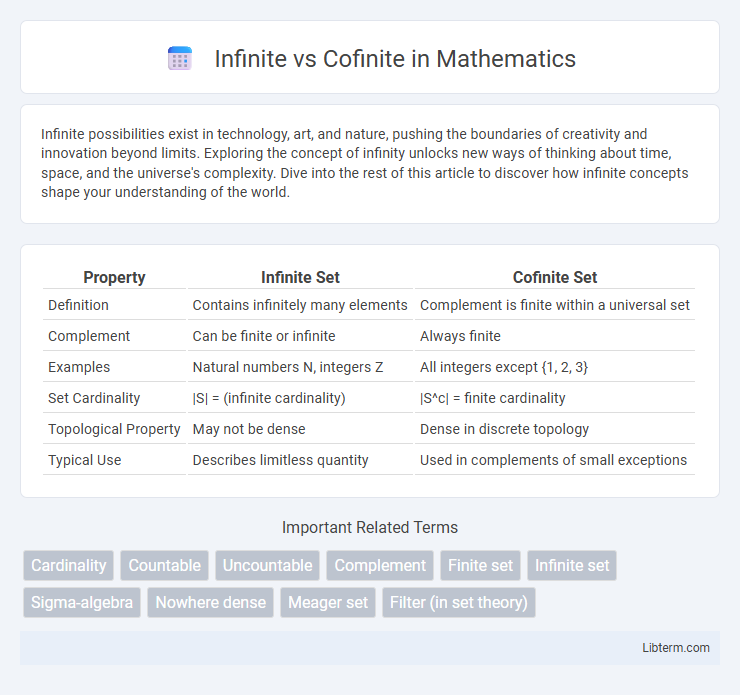
| Property | Infinite Set | Cofinite Set |
|---|---|---|
| Definition | Contains infinitely many elements | Complement is finite within a universal set |
| Complement | Can be finite or infinite | Always finite |
| Examples | Natural numbers N, integers Z | All integers except {1, 2, 3} |
| Set Cardinality | |S| = (infinite cardinality) | |S^c| = finite cardinality |
| Topological Property | May not be dense | Dense in discrete topology |
| Typical Use | Describes limitless quantity | Used in complements of small exceptions |
Understanding Infinite and Cofinite Sets
Infinite sets contain an unlimited number of elements, such as the set of natural numbers, whereas cofinite sets are defined by having a finite complement relative to a universal set, meaning all but finitely many elements are included. Understanding infinite and cofinite sets involves recognizing that while infinite sets extend without bound, cofinite sets remain large but exclude only a finite subset. These concepts are fundamental in set theory, particularly in topology and combinatorics, where cofinite sets often help characterize dense or residual properties.
Definitions: Infinite vs Cofinite
Infinite sets contain an uncountable or countably endless number of elements, such as the set of natural numbers or real numbers. Cofinite sets are defined as subsets of a given universal set whose complements are finite, meaning they include all but a finite number of elements from the universal set. Understanding the distinction between infinite and cofinite sets is fundamental in set theory and topology for analyzing convergence and density properties.
Fundamental Properties of Infinite Sets
Infinite sets, such as the set of natural numbers, contain an unbounded number of elements without a finite limit, contrasting with cofinite sets whose complements are finite. Fundamental properties of infinite sets include their ability to be put into a one-to-one correspondence with proper subsets, exemplified by Hilbert's Hotel paradox. These properties highlight the non-intuitive nature of infinite cardinalities and their role in set theory, particularly in distinguishing countable from uncountable infinities.
Key Characteristics of Cofinite Sets
Cofinite sets are characterized by having complements that are finite, meaning all but a finite number of elements from the universal set are included. These sets play a crucial role in topology and analysis, particularly in defining cofinite topologies where open sets are either cofinite or empty. Their structure ensures that they are infinite unless the entire universal set is finite, distinguishing them from infinite sets whose complements can also be infinite.
Infinite vs Cofinite: Core Differences
Infinite sets contain an unbounded number of elements, such as the set of natural numbers, whereas cofinite sets have complements that are finite, meaning the difference between the universal set and the cofinite set is a finite set. The core difference lies in the structure of their complements: infinite sets can have either infinite or finite complements, but cofinite sets specifically require a finite complement. This distinction impacts set operations and properties in fields like topology and measure theory, where understanding the finiteness of complements is critical.
Examples of Infinite Sets in Mathematics
Infinite sets in mathematics include the set of natural numbers \( \mathbb{N} = \{1, 2, 3, \ldots\} \), integers \( \mathbb{Z} \), rational numbers \( \mathbb{Q} \), and real numbers \( \mathbb{R} \). These sets contrast with cofinite sets, which have complements that are finite; for example, the set of all integers except for a finite number of specific values is cofinite. The cardinality of infinite sets like \( \mathbb{N} \) and \( \mathbb{R} \) varies, with \( \mathbb{N} \) being countably infinite and \( \mathbb{R} \) uncountably infinite, illustrating different concepts of infinity in set theory.
Real-World Illustrations of Cofinite Sets
Cofinite sets appear frequently in computer science, such as the set of all strings over a finite alphabet except a finite number of invalid or forbidden sequences, illustrating their utility in language processing and error detection. In network theory, the collection of all nodes except a finite set of faulty or disconnected nodes demonstrates cofinite set concepts in ensuring robust communication. These examples emphasize how cofinite sets provide a framework for managing exceptions within infinite structures in practical scenarios.
Set Operations: Infinite and Cofinite Contexts
Infinite sets remain unchanged under union with any cofinite set because the union covers almost the entire universal set. Intersection of a cofinite set with an infinite set often results in an infinite set, as removing finitely many elements from an infinite set preserves its infinitude. The complement of a cofinite set is finite, while the complement of an infinite set is typically infinite, highlighting contrasting behaviors in set difference operations.
Infinite and Cofinite in Topology
Infinite sets in topology refer to collections with an unbounded number of elements, essential for studying concepts like limit points and convergence in infinite spaces. Cofinite topology is a particular type of topology where closed sets are either the whole space or finite, making the complements (open sets) infinite, providing a simple yet powerful structure to analyze continuity and compactness. Understanding the relationship between infinite sets and the cofinite topology helps in exploring fundamental properties such as connectedness and separation axioms in infinite topological spaces.
Applications and Significance of Infinite vs Cofinite
Infinite sets are pivotal in mathematical analysis and computer science for modeling unbounded processes and structures, such as infinite sequences and languages. Cofinite sets, whose complements are finite, are essential in topology and number theory for defining dense subsets and convergence criteria, often simplifying problems by ignoring finite exceptions. Understanding the distinction between infinite and cofinite sets enhances algorithm design, particularly in optimization and complexity theory, where handling large or nearly complete data efficiently is crucial.
Infinite Infographic
 libterm.com
libterm.com