Infinity represents a concept that transcends numerical limits, symbolizing endlessness in mathematics, physics, and philosophy. Understanding infinity helps you grasp complex ideas such as infinite series, boundless space, and perpetual growth. Explore the rest of this article to uncover the profound implications and applications of infinity in various fields.
Table of Comparison
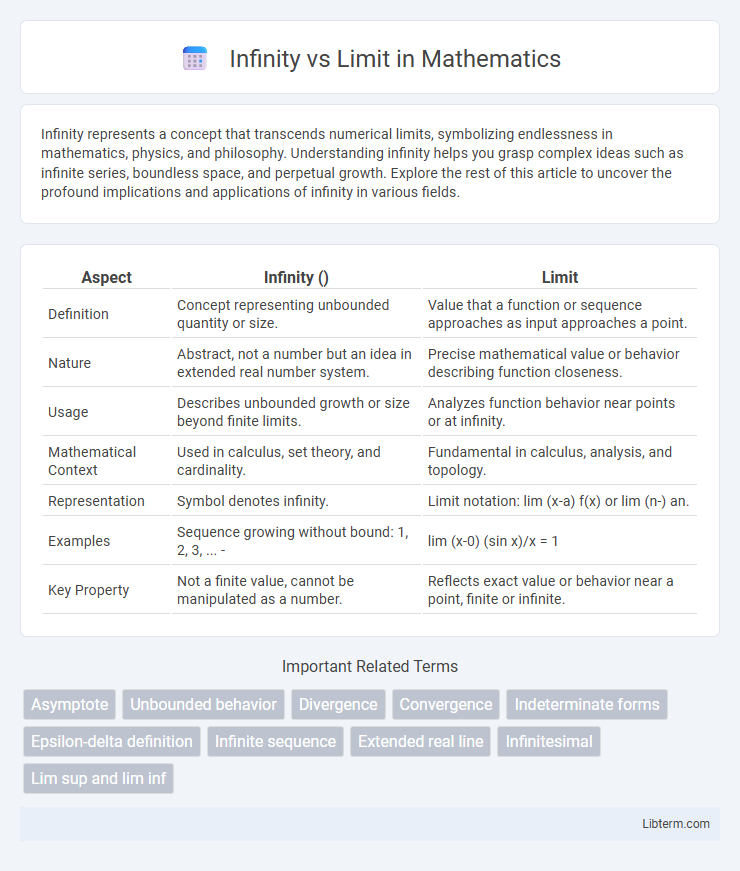
| Aspect | Infinity () | Limit |
|---|---|---|
| Definition | Concept representing unbounded quantity or size. | Value that a function or sequence approaches as input approaches a point. |
| Nature | Abstract, not a number but an idea in extended real number system. | Precise mathematical value or behavior describing function closeness. |
| Usage | Describes unbounded growth or size beyond finite limits. | Analyzes function behavior near points or at infinity. |
| Mathematical Context | Used in calculus, set theory, and cardinality. | Fundamental in calculus, analysis, and topology. |
| Representation | Symbol denotes infinity. | Limit notation: lim (x-a) f(x) or lim (n-) an. |
| Examples | Sequence growing without bound: 1, 2, 3, ... - | lim (x-0) (sin x)/x = 1 |
| Key Property | Not a finite value, cannot be manipulated as a number. | Reflects exact value or behavior near a point, finite or infinite. |
Understanding Infinity: Concept and Definition
Infinity represents an unbounded quantity that transcends finite numbers, often described as a concept rather than a specific value. It is used in mathematics to signify endlessness, such as in sets, sequences, or limits that grow without bound. Unlike limits, which approach a particular value or infinity, infinity itself is an abstract notion embodying limitless magnitude.
The Limit: Foundational Principle in Calculus
The limit is a foundational principle in calculus that enables the precise definition of continuity, derivatives, and integrals by examining the behavior of functions as inputs approach a specific value. Unlike infinity, which represents unbounded growth, a limit evaluates the finite value that a function approaches, providing critical insight into function behavior near points of interest. Understanding limits allows mathematicians to rigorously analyze instantaneous rates of change and accumulate quantities, forming the core of differential and integral calculus.
Infinity vs. Limit: Key Differences
Infinity represents an unbounded quantity that grows without limit, while a limit describes the value a function approaches as the input nears a specific point. Limits can approach finite numbers or infinity, serving as a foundational concept in calculus to analyze continuity and behavior near singularities. Understanding this distinction is critical in mathematical analysis, as infinity is not a number but a concept, whereas limits provide a precise method for evaluating function behavior.
Historical Evolution of Infinity and Limits
The historical evolution of infinity and limits traces back to ancient Greek mathematicians like Zeno and Aristotle, who grappled with paradoxes involving infinite divisibility. During the 17th century, calculus pioneers such as Newton and Leibniz formalized limits to rigorously handle infinite processes, laying the foundation for modern mathematical analysis. The 19th century witnessed further refinement with Cauchy and Weierstrass defining limits using epsilon-delta notation, solidifying the rigorous treatment of infinity in calculus.
Mathematical Representation: Symbols and Notation
Infinity is denoted by the symbol , representing an unbounded quantity beyond any finite value, while limits use the notation lim followed by a variable approaching a specific value or infinity, such as limx-a or limx-. Limits describe the behavior of a function as the input approaches a particular point, expressed symbolically to define convergence or divergence. The interplay between and limit notation is crucial in calculus, particularly in defining concepts like infinite limits and limits at infinity.
Real-Life Applications of Infinity and Limit
In real-life applications, infinity represents concepts like unbounded growth or endless processes, such as population models and cosmic distances, where values grow beyond any finite limit. Limits are crucial in fields like engineering and physics to analyze behavior as variables approach specific points, such as calculating instantaneous velocity or electrical current at a precise moment. Both infinity and limits enable precise modeling of continuous change and extreme cases in technology, economics, and natural sciences.
Philosophical Implications: Infinity Beyond Mathematics
Infinity transcends mathematical boundaries, embodying an abstract concept that challenges human comprehension of the infinite and the finite. Philosophers explore infinity as a metaphor for boundlessness in existence, time, and knowledge, revealing paradoxes about the nature of reality and the limits of human cognition. The distinction between infinity and limit illuminates profound questions about the continuity of experience and the infinite potential of being beyond quantifiable measurement.
Common Misconceptions about Infinity and Limits
Infinity is not a specific number but a concept representing unbounded growth, while limits describe the behavior of functions as inputs approach a certain value. A common misconception is treating infinity as a reachable value rather than an idea of endlessness, leading to misunderstandings in evaluating limits. Limits involving infinity often address how functions behave near infinity or near points where values grow without bound, not implying that infinity itself is attainable.
Importance in Advanced Mathematics and Science
Infinity represents an unbounded quantity essential in advanced mathematics for describing limits, continuity, and series convergence, while limits rigorously define the behavior of functions as inputs approach specific points or infinity. Understanding the distinction enables precise formulation of calculus concepts, such as derivatives and integrals, which are foundational in physics and engineering. Mastery of infinity and limits facilitates modeling complex phenomena, including asymptotic analysis and infinite-dimensional spaces in advanced scientific research.
Infinity or Limit: Which Is More Fundamental?
Limits are more fundamental in calculus because they rigorously define the behavior of functions as inputs approach specific values or infinity, providing the foundation for continuity, derivatives, and integrals. Infinity serves as a concept or symbol representing unbounded growth or size, but it lacks the precise operational framework that limits offer in analysis. Understanding limits enables mathematicians to handle infinite processes and approximate values near undefined points, making limits essential to advanced mathematical reasoning.
Infinity Infographic
 libterm.com
libterm.com