Non-metric data refers to information that cannot be quantified or measured on a numerical scale, often including categorical variables such as colors, labels, or classifications. Analyzing non-metric data requires specialized techniques like qualitative analysis, cluster analysis, or multidimensional scaling to extract meaningful patterns. Explore the rest of the article to learn how non-metric approaches can enhance your data analysis strategy.
Table of Comparison
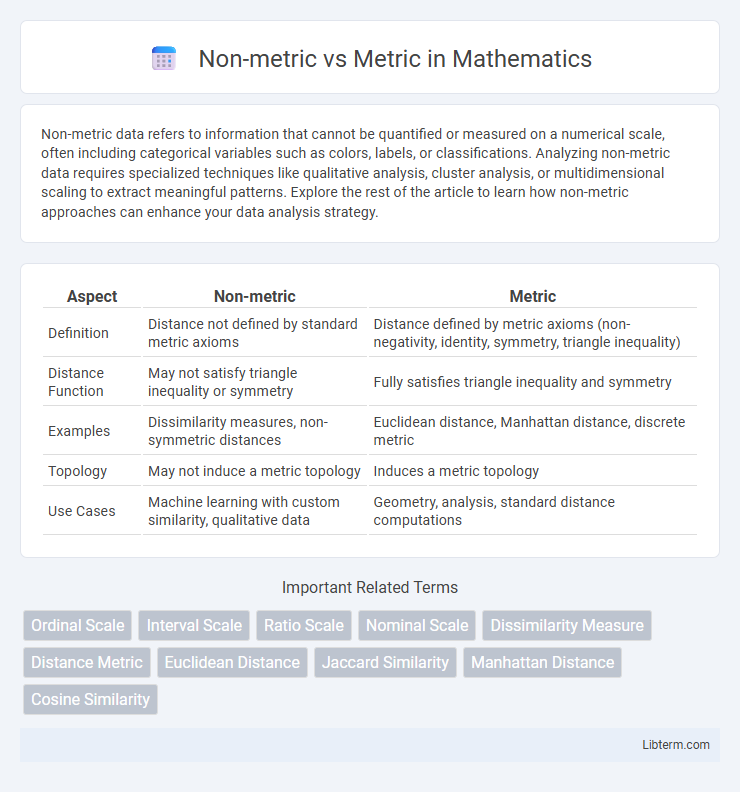
| Aspect | Non-metric | Metric |
|---|---|---|
| Definition | Distance not defined by standard metric axioms | Distance defined by metric axioms (non-negativity, identity, symmetry, triangle inequality) |
| Distance Function | May not satisfy triangle inequality or symmetry | Fully satisfies triangle inequality and symmetry |
| Examples | Dissimilarity measures, non-symmetric distances | Euclidean distance, Manhattan distance, discrete metric |
| Topology | May not induce a metric topology | Induces a metric topology |
| Use Cases | Machine learning with custom similarity, qualitative data | Geometry, analysis, standard distance computations |
Introduction to Metric and Non-Metric Concepts
Metric concepts rely on numerical distances that satisfy properties like non-negativity, identity, symmetry, and the triangle inequality to quantify similarity or dissimilarity. Non-metric concepts involve relationships that do not adhere strictly to these distance axioms, often based on ordinal or qualitative comparisons rather than precise measurements. Understanding these distinctions is essential for choosing appropriate models in fields like machine learning, data analysis, and pattern recognition.
Defining Metrics: Overview and Characteristics
Defining metrics involves establishing a quantitative measure that adheres to properties such as non-negativity, identity of indiscernibles, symmetry, and the triangle inequality, ensuring accurate evaluation of distances in metric spaces. Non-metric measures, however, relax these constraints, allowing for asymmetry or violations of the triangle inequality, which is useful in contexts like similarity assessments or when data relationships are non-linear. Understanding the distinctions between metric and non-metric definitions enables more effective selection of distance functions tailored to specific analytical or computational tasks.
Understanding Non-Metric Measurements
Non-metric measurements do not rely on numerical scales but instead use qualitative or descriptive attributes, such as color, texture, or taste, which are essential for subjective assessments in fields like sensory evaluation and anthropology. Understanding non-metric measurements involves recognizing their role in capturing data that cannot be quantified but provides valuable insights through categories or rankings. These measurements complement metric data by enabling analyses that incorporate human perception and categorical variables, enhancing the depth and breadth of research outcomes.
Key Differences Between Metric and Non-Metric Methods
Metric methods rely on numerical data and distances measured using precise scales, enabling quantitative analysis and mathematical computations. Non-metric methods handle qualitative or categorical data, focusing on the order or rank rather than exact values, often used in ordinal or nominal data analysis. The key difference lies in metric methods requiring interval or ratio data for accurate measurement, while non-metric methods are suitable for non-numeric or unordered data sets.
Applications of Metric Techniques
Metric techniques, which involve distance measures satisfying properties like non-negativity, identity, symmetry, and triangle inequality, find extensive applications in clustering, image recognition, and recommender systems. Algorithms such as k-means clustering and k-nearest neighbors rely on Euclidean or Manhattan distances to effectively group similar data points or classify objects based on proximity. These metric-based methods enhance accuracy and computational efficiency in high-dimensional data analysis and spatial data mining.
Use Cases for Non-Metric Approaches
Non-metric approaches excel in handling data with ordinal, categorical, or qualitative attributes where precise numeric distances lack meaning, such as customer satisfaction surveys or preference rankings. These methods are particularly useful in clustering social science research data, recommendation systems based on user behavior, and bioinformatics for analyzing genetic marker similarities. Non-metric techniques enable flexible similarity assessments without relying on Euclidean distances, making them ideal for heterogeneous datasets and complex relational patterns.
Advantages and Limitations of Metric Systems
Metric systems offer standardized and universally accepted units, facilitating consistency and ease of communication in scientific and industrial applications worldwide. Their decimal-based structure simplifies calculations and conversions, increasing efficiency and reducing errors compared to non-metric systems. However, metric units may face limitations in specific cultural contexts or industries where traditional or imperial measurements remain customary, potentially causing adaptation challenges.
Benefits and Drawbacks of Non-Metric Systems
Non-metric systems offer flexibility and simplicity, making them ideal for qualitative assessments and categories without inherent numerical order. They excel in scenarios where subjective judgment or nominal classification is required but struggle with precision, consistency, and scaling compared to metric systems. The main drawback is their limited ability to support quantitative analysis, leading to challenges in statistical measurements and interoperability with metric-based frameworks.
Choosing Between Metric and Non-Metric: Factors to Consider
Choosing between metric and non-metric depends on the nature of the data and the analysis goals; metric measures require interval or ratio scales with consistent differences, while non-metric measures apply to ordinal or nominal data without assuming equal intervals. Consider the data type, measurement scale, and whether the analysis demands precise distance calculations or relative rankings to determine the appropriate approach. Computational complexity and interpretability also influence the decision, as metric methods often yield more nuanced results but require stricter data assumptions.
Conclusion: Which to Use—Metric or Non-Metric?
Choosing between metric and non-metric methods depends on data type and analysis goals; metric techniques are ideal for numerical data with meaningful distances, enabling precise calculations and optimization. Non-metric approaches excel with ordinal or categorical data, preserving rank order without assuming equal intervals, making them suitable for qualitative or non-linear relationships. Prioritize metric methods for quantitative accuracy and computational efficiency, and non-metric methods for flexibility and robustness with diverse data structures.
Non-metric Infographic
 libterm.com
libterm.com