Algebraic concepts form the foundation of advanced mathematics, enabling you to solve equations and understand relationships between variables efficiently. Mastery of algebraic techniques is essential for success in fields ranging from engineering to economics. Explore the rest of the article to deepen your understanding of algebraic principles and their practical applications.
Table of Comparison
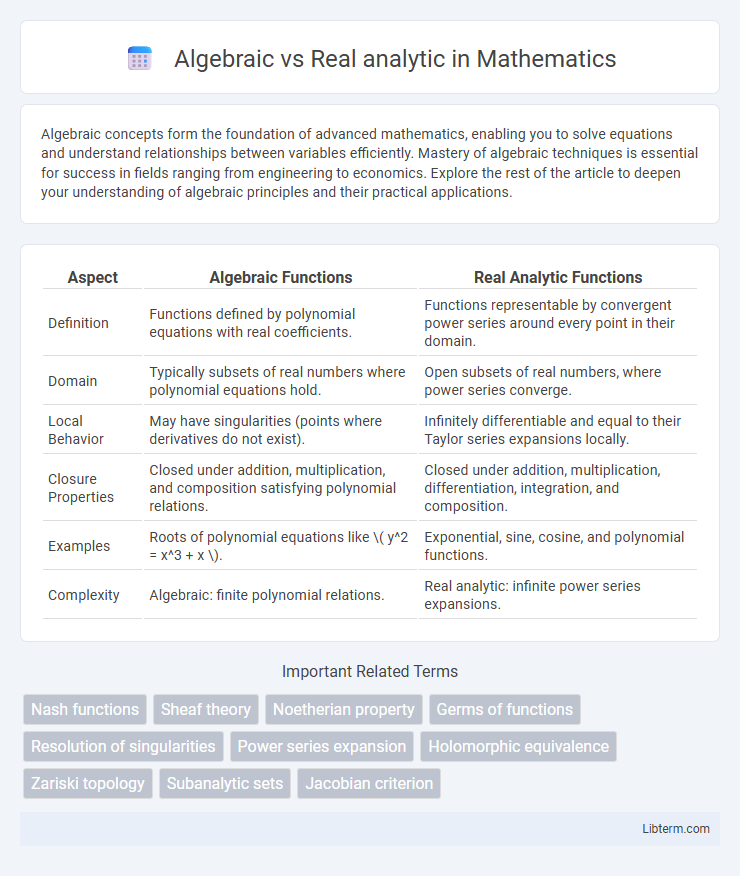
| Aspect | Algebraic Functions | Real Analytic Functions |
|---|---|---|
| Definition | Functions defined by polynomial equations with real coefficients. | Functions representable by convergent power series around every point in their domain. |
| Domain | Typically subsets of real numbers where polynomial equations hold. | Open subsets of real numbers, where power series converge. |
| Local Behavior | May have singularities (points where derivatives do not exist). | Infinitely differentiable and equal to their Taylor series expansions locally. |
| Closure Properties | Closed under addition, multiplication, and composition satisfying polynomial relations. | Closed under addition, multiplication, differentiation, integration, and composition. |
| Examples | Roots of polynomial equations like \( y^2 = x^3 + x \). | Exponential, sine, cosine, and polynomial functions. |
| Complexity | Algebraic: finite polynomial relations. | Real analytic: infinite power series expansions. |
Introduction to Algebraic and Real Analytic Functions
Algebraic functions are defined as roots of polynomial equations with coefficients in a given field, showcasing properties such as being closed under addition, multiplication, and composition within that field. Real analytic functions, characterized by convergent power series expansions in a neighborhood of every point in their domain, extend beyond algebraic functions by allowing infinite differentiability and local representability via analytic continuation. Understanding the differences between algebraic and real analytic functions is crucial in complex analysis and differential geometry, where the analytic structure governs local behavior and algebraic properties determine global constraints.
Defining Algebraic Functions: Key Concepts
Algebraic functions are defined as solutions to polynomial equations with coefficients in a given field, typically the complex or real numbers, distinguishing them from real analytic functions that are locally represented by convergent power series. Key concepts in defining algebraic functions include irreducibility of the polynomial, algebraic closure, and the algebraic variety where the function satisfies the polynomial relation. These functions exhibit algebraic structure and are crucial in fields such as algebraic geometry, contrasting with real analytic functions that emphasize differentiability and analytic continuation in real or complex domains.
Understanding Real Analytic Functions
Real analytic functions can be expressed as convergent power series within their radius of convergence, providing a precise local representation that distinguishes them from algebraic functions, which satisfy polynomial equations with coefficients in a given field. Understanding real analytic functions involves recognizing their infinite differentiability and the correspondence between their Taylor series and function values in a neighborhood, enabling exact analytic continuation. This contrasts with algebraic functions that may have branch points and singularities, highlighting the broader flexibility and completeness of real analytic function theory in real analysis and differential equations.
Main Differences Between Algebraic and Real Analytic Functions
Algebraic functions are defined as solutions to polynomial equations with coefficients in a given field, often characterized by their finite degree and algebraic expressions. Real analytic functions, on the other hand, are infinitely differentiable and locally expressible as convergent power series with real coefficients, capturing a broader class of smooth functions beyond algebraic constraints. The main differences lie in their definitional scope--algebraic functions satisfy polynomial relations globally, while real analytic functions satisfy local analyticity and smoothness without necessarily being algebraic.
Examples of Algebraic Functions
Algebraic functions are defined as functions that satisfy a polynomial equation with coefficients as polynomials themselves, such as f(x) = (x^2 + 1) or f(x) = (x^3 - 2x + 1)^(1/2). Real analytic functions, in contrast, are represented by convergent power series around any point in their domain, including transcendental functions like e^x or sin(x). Examples of algebraic functions include polynomials like f(x) = x^3 - 4x + 1 and roots like f(x) = (x^2 + 2)^(1/3), both ensuring algebraic equations with explicit polynomial terms.
Notable Real Analytic Function Examples
Notable real analytic functions include exponential, trigonometric, and logarithmic functions, each expressible as convergent power series around points in their domains. Algebraic functions satisfy polynomial equations with coefficients that are themselves polynomials, such as polynomials and roots, differentiating them from more general real analytic functions like \( e^x \) or \(\sin x\), which are transcendental. Real analytic functions are infinitely differentiable and locally equal to their Taylor series, representing a broader class that encompasses but extends beyond algebraic functions.
Singularities and Extension Properties
Algebraic functions exhibit singularities that are typically algebraic branch points or poles described by polynomial equations, while real analytic functions may have more intricate singularities characterized by convergent power series expansions with radius of convergence constraints. Singularities of algebraic functions are algebraically determined and often allow algebraic continuation via analytic continuation along paths avoiding branch cuts, whereas real analytic functions exhibit extension properties primarily governed by the real analyticity radius and complexification. The extension of algebraic functions beyond singular points frequently manifests through algebraic Riemann surfaces, contrasting with the local extendability of real analytic functions relying on real analyticity and complex analytic continuation in multidimensional spaces.
Applications in Mathematics and Science
Algebraic functions, defined by polynomial equations, play a crucial role in solving problems in algebraic geometry and number theory, enabling precise modeling of polynomial-based structures and varieties. Real analytic functions, characterized by convergent power series expansions, are essential in differential equations and dynamical systems, providing smooth approximations and local behavior analysis critical in physics and engineering. Both function classes underpin mathematical frameworks for modeling natural phenomena, with algebraic functions excelling in discrete structures and real analytic functions in continuous, smooth processes.
Limitations and Open Questions
Algebraic functions are defined by polynomial equations with finite degrees, limiting their expressiveness compared to real analytic functions, which possess convergent power series expansions around points in their domain. Real analytic functions can model a broader range of phenomena due to infinite differentiability and local representability by Taylor series, but challenges persist in characterizing which real analytic functions correspond to algebraic ones. Key open questions involve the boundary between algebraic and transcendental analytic functions, criteria for algebraicity within analytic sets, and computational complexity in identifying algebraic identities among real analytic functions.
Summary: Choosing Algebraic or Real Analytic Functions
Algebraic functions are defined by polynomial equations with coefficients in a given field, offering exact solutions and strong structural properties ideal for symbolic computation and algebraic geometry. Real analytic functions, characterized by locally convergent power series expansions, provide powerful tools for representing smooth behavior and solving differential equations with high precision. Selecting between algebraic and real analytic functions depends on the problem's nature: algebraic for discrete, exact algebraic structures, and real analytic for continuous, smooth phenomena requiring detailed local approximations.
Algebraic Infographic
 libterm.com
libterm.com