Topology explores properties of space that are preserved under continuous deformations such as stretching or bending, without tearing or gluing. It has profound applications in fields like mathematics, physics, and computer science, influencing concepts from network theory to quantum computing. Dive into this article to discover how topology shapes the world around you and unlock new perspectives on spatial relationships.
Table of Comparison
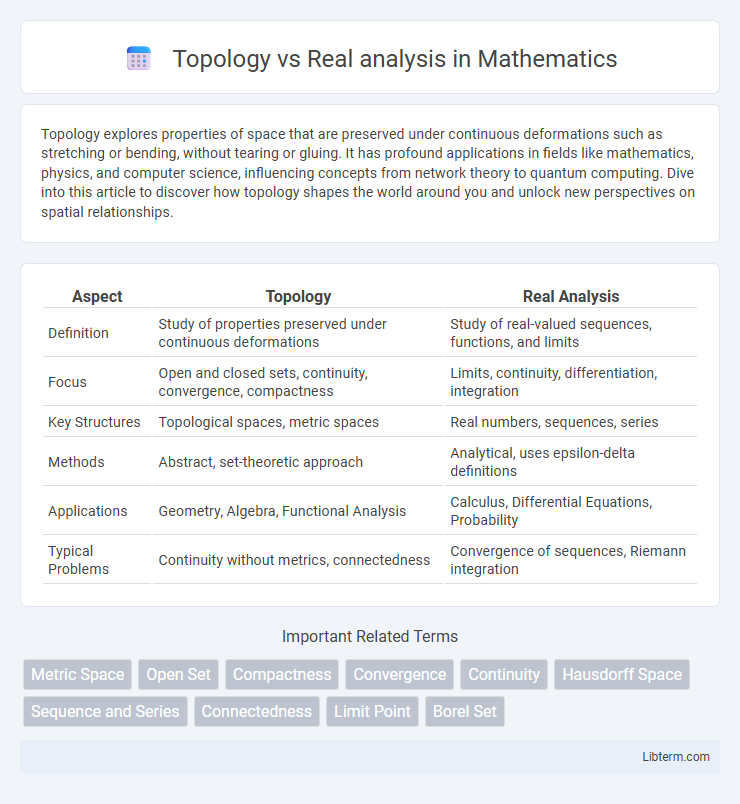
| Aspect | Topology | Real Analysis |
|---|---|---|
| Definition | Study of properties preserved under continuous deformations | Study of real-valued sequences, functions, and limits |
| Focus | Open and closed sets, continuity, convergence, compactness | Limits, continuity, differentiation, integration |
| Key Structures | Topological spaces, metric spaces | Real numbers, sequences, series |
| Methods | Abstract, set-theoretic approach | Analytical, uses epsilon-delta definitions |
| Applications | Geometry, Algebra, Functional Analysis | Calculus, Differential Equations, Probability |
| Typical Problems | Continuity without metrics, connectedness | Convergence of sequences, Riemann integration |
Introduction to Topology and Real Analysis
Topology studies properties of space that remain invariant under continuous deformations, focusing on concepts like open and closed sets, continuity, and convergence. Real analysis delves into the rigorous examination of real numbers, sequences, series, and functions, emphasizing limits, differentiation, and integration. Both fields form foundational pillars in modern mathematics, with topology providing abstract frameworks that enrich the understanding of real analysis.
Fundamental Concepts in Topology
Fundamental concepts in topology include open and closed sets, continuity, and convergence, which provide a flexible framework for studying spatial properties independent of exact distances. Unlike real analysis, which emphasizes limits, sequences, and metric spaces with precise numeric structure, topology focuses on qualitative aspects such as connectedness and compactness. These foundational ideas enable mathematicians to generalize limits and continuity beyond the real number line, forming the basis for more abstract mathematical analysis.
Core Principles of Real Analysis
Real analysis centers on rigorously defining and analyzing limits, continuity, differentiation, and integration of real-valued functions, emphasizing e-d arguments and sequence convergence. It relies on the completeness of the real number system and the precise behavior of functions on intervals within R. Topology, while related, abstracts these notions to more general spaces, focusing on open sets and continuity without requiring a metric or order structure.
Key Differences Between Topology and Real Analysis
Topology studies the properties of spaces invariant under continuous deformations, focusing on concepts like open sets, continuity, and convergence without relying on specific distances. Real analysis centers on the rigorous study of real numbers, sequences, and functions, emphasizing limits, derivatives, integrals, and measure theory based on the metric structure of the real line. While topology provides a broader framework for analyzing spaces abstractly, real analysis applies metric and order properties of the real numbers to solve problems in calculus and function behavior.
Role of Continuity in Topology and Real Analysis
Continuity in topology is defined through open sets, where a function is continuous if the preimage of every open set is open, emphasizing the abstract and general nature of continuity beyond metric spaces. In real analysis, continuity relies on the epsilon-delta definition, providing a precise numerical approach to limits and function behavior on the real number line. Both fields use continuity to study function properties, but topology abstracts continuity to broader contexts while real analysis focuses on detailed quantitative behavior.
Importance of Open and Closed Sets
Open and closed sets form the foundational concepts in both topology and real analysis, defining the structure of spaces and continuity of functions. In topology, open sets generate the topology and determine properties such as convergence, compactness, and connectedness, while in real analysis, open and closed intervals underpin limits, continuity, and differentiation. Mastery of these sets enables a deep understanding of metric spaces, convergence criteria, and the behavior of functions across both mathematical disciplines.
Convergence in Topology vs Real Analysis
Convergence in topology generalizes sequences and nets by focusing on open sets and neighborhood systems rather than specific coordinate values. Real analysis convergence is typically defined through limits of sequences or series in metric spaces like \(\mathbb{R}\), using epsilon-delta criteria for precision. Topological convergence allows for broader applications in spaces lacking metric structure, emphasizing continuity and closure properties beyond numeric limits.
Applications in Mathematics and Beyond
Topology provides a framework for studying properties of space that are preserved under continuous transformations, which is fundamental in areas like algebraic topology, differential geometry, and dynamical systems. Real analysis focuses on the rigorous study of limits, continuity, and measure, underpinning fields such as calculus, functional analysis, and probability theory. Together, these disciplines drive advancements in mathematical physics, data science, and engineering by enabling precise modeling of complex structures and continuous phenomena.
Typical Problems and Theorems
Topology deals with properties of spaces preserved under continuous deformations, focusing on problems like classifying topological spaces and studying continuity, compactness, and connectedness, with key theorems including the Brouwer Fixed Point Theorem and Urysohn's Lemma. Real analysis addresses the rigorous study of real-valued functions, limits, integration, and sequences, with typical problems involving convergence, differentiation, and measure theory, underpinned by fundamental theorems such as the Intermediate Value Theorem, the Lebesgue Dominated Convergence Theorem, and the Fundamental Theorem of Calculus. While topology emphasizes qualitative spatial properties and abstract spaces, real analysis centers on quantitative properties of functions and numerical limits within real number systems.
Choosing Between Topology and Real Analysis
Choosing between topology and real analysis depends on your mathematical interests and career goals; topology emphasizes abstract properties of space and continuity while real analysis focuses on rigorous study of limits, sequences, and functions. Students interested in geometric intuition and qualitative aspects of spaces often gravitate towards topology, whereas those drawn to function behavior, measure theory, and integration typically prefer real analysis. Understanding core concepts like open and closed sets in topology or convergence and differentiability in real analysis helps tailor your choice to suit research or applied mathematics objectives.
Topology Infographic
 libterm.com
libterm.com