Hereditarily finite sets are finite sets whose elements are also hereditarily finite, forming a well-founded hierarchy. These sets are fundamental in mathematical logic and computer science, representing objects built from the empty set through finitely many operations. Explore the rest of the article to understand how hereditarily finite sets underpin key theories and applications.
Table of Comparison
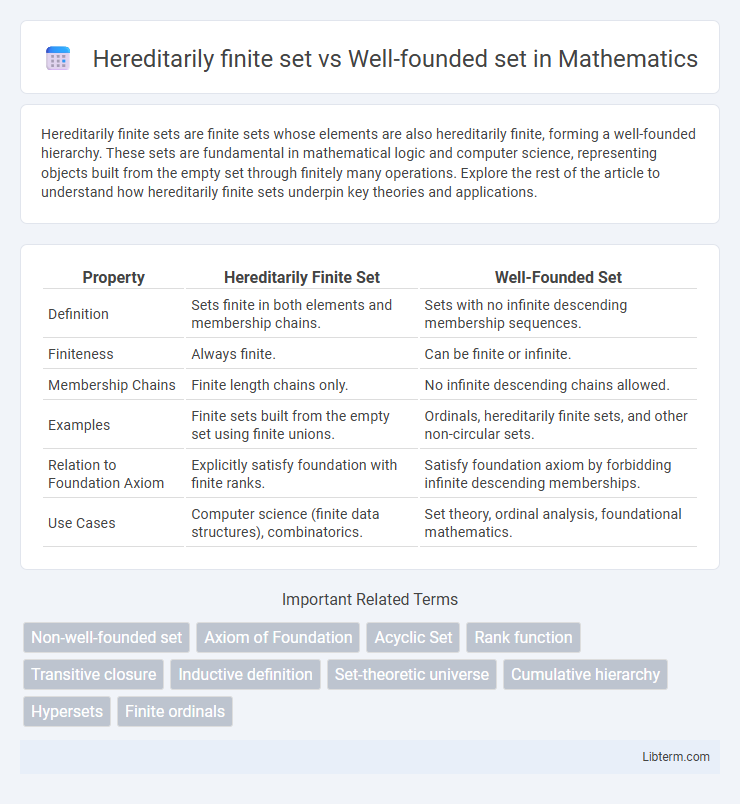
| Property | Hereditarily Finite Set | Well-Founded Set |
|---|---|---|
| Definition | Sets finite in both elements and membership chains. | Sets with no infinite descending membership sequences. |
| Finiteness | Always finite. | Can be finite or infinite. |
| Membership Chains | Finite length chains only. | No infinite descending chains allowed. |
| Examples | Finite sets built from the empty set using finite unions. | Ordinals, hereditarily finite sets, and other non-circular sets. |
| Relation to Foundation Axiom | Explicitly satisfy foundation with finite ranks. | Satisfy foundation axiom by forbidding infinite descending memberships. |
| Use Cases | Computer science (finite data structures), combinatorics. | Set theory, ordinal analysis, foundational mathematics. |
Introduction to Hereditarily Finite Sets
Hereditarily finite sets are defined as finite sets whose elements are also hereditarily finite, resulting in structures built exclusively from finite stages without infinite descending membership chains. These sets form the smallest transitive class containing the empty set and are closed under finite union and power set operations, ensuring their finiteness at every level. Unlike well-founded sets, which prohibit infinite membership chains but can be infinite themselves, hereditarily finite sets are strictly finite and foundational in computability theory and finite model theory.
Understanding Well-Founded Sets
Well-founded sets are defined by the absence of infinitely descending membership chains, ensuring every non-empty subset has a minimal element under the membership relation. Hereditarily finite sets, a subclass of well-founded sets, consist exclusively of finite sets whose elements are also hereditarily finite, making them strictly finite in nature. Understanding well-founded sets involves grasping their foundational role in set theory by preventing infinite regress and supporting inductive definitions.
Key Differences Between Hereditarily Finite and Well-Founded Sets
Hereditarily finite sets are finite sets whose elements are also hereditarily finite, ensuring no infinite descending chains and all sets have a finite rank. Well-founded sets generalize this by allowing infinite sets but prohibit infinitely descending membership sequences, preserving foundation through the well-foundedness axiom. The key difference lies in finiteness: hereditarily finite sets are strictly finite and built from the empty set using finitely many operations, while well-founded sets include infinite structures as long as there is no infinite descending -sequence.
Mathematical Definitions and Formalisms
Hereditarily finite sets are defined as finite sets whose elements are also hereditarily finite, forming a cumulative hierarchy indexed by natural numbers, ensuring no infinite descending membership chains. Well-founded sets are characterized by the absence of infinite descending sequences under the membership relation, formalized through the foundation axiom in Zermelo-Fraenkel set theory, guaranteeing every non-empty set has an -minimal element. While all hereditarily finite sets are well-founded, well-foundedness encompasses a broader class including infinite sets, emphasizing foundational principles in set-theoretic constructions.
Examples Illustrating Hereditarily Finite Sets
Hereditarily finite sets are finite sets whose elements are also hereditarily finite, such as the empty set , the set {}, and the set {{}, }. Each element within a hereditarily finite set is itself a finite set, built up from the empty set through a finite number of steps, exemplifying the iterative nature of these sets. Unlike general well-founded sets, which prohibit infinite descending membership chains, hereditarily finite sets are strictly finite and provide concrete examples of well-foundedness in a finite context.
Properties and Structure of Well-Founded Sets
Well-founded sets are characterized by the absence of infinite descending membership chains, ensuring that every non-empty subset has a minimal element, which guarantees a foundation axiom is satisfied in Zermelo-Fraenkel set theory. Unlike hereditarily finite sets, which are strictly finite and constructed from finite elements only, well-founded sets may be infinite and structurally more complex, supporting transfinite constructions and recursive definitions. The well-foundedness property enables inductive proofs and recursion on sets, providing a robust framework for defining rank functions and hierarchical set structures critical in foundational mathematics.
Applications in Set Theory and Computer Science
Hereditarily finite sets, which are finite sets whose elements are also hereditarily finite, play a crucial role in formalizing finite data structures and algorithms within computer science, particularly in areas such as automated reasoning, database theory, and programming language semantics. Well-founded sets, characterized by the absence of infinitely descending membership chains, underpin foundational proofs in set theory and enable the construction of recursive definitions and induction principles essential for verifying program correctness and termination. Both concepts facilitate modeling hierarchical structures, with hereditarily finite sets providing a framework for finite model theory and well-founded sets ensuring soundness in transfinite induction and well-founded recursion used in formal verification.
Hierarchical Relationships and Ordinals
Hereditarily finite sets are constructed through finite iterations of the power set operation, ensuring each member is finite and well-founded without infinite descending membership chains. Well-founded sets generalize this concept by allowing infinite hierarchies while still prohibiting infinitely descending membership sequences, forming a foundation for ordinal analysis. Ordinals represent the position within these well-founded hierarchical structures, encoding the order types that arise from transfinite recursion on such sets.
Limitations and Challenges in Comparison
Hereditarily finite sets are restricted by their finite nature, limiting their expressiveness to finite structures and making them unsuitable for modeling infinite or more complex hierarchies inherent in well-founded sets. Well-founded sets can represent infinite descending chains and support transfinite induction, but their complexity introduces challenges in computability and practical implementation. The comparison reveals that hereditarily finite sets excel in computational simplicity, while well-founded sets face limitations related to infinite regress and ensuring foundational stability.
Conclusion: Implications for Set Theory
Hereditarily finite sets form a foundational class in set theory characterized by finite elements and finite rank, providing a concrete framework for computational models and finite combinatorics. Well-founded sets, defined by the absence of infinitely descending membership chains, underpin the standard cumulative hierarchy and support the axiom of foundation, ensuring consistency in classical set theory. The distinction highlights crucial implications: hereditarily finite sets offer a tractable subset for algorithmic applications, while well-founded sets establish a broader structure essential for the development of ordinal and transfinite analysis within set theory.
Hereditarily finite set Infographic
 libterm.com
libterm.com