Congruence in mathematics refers to the relationship between two figures or numbers that have the same size and shape or yield the same remainder when divided by a certain number. Understanding congruence is essential for solving problems in geometry, number theory, and modular arithmetic. Explore the rest of the article to discover how congruence applies to various mathematical concepts and enhances your problem-solving skills.
Table of Comparison
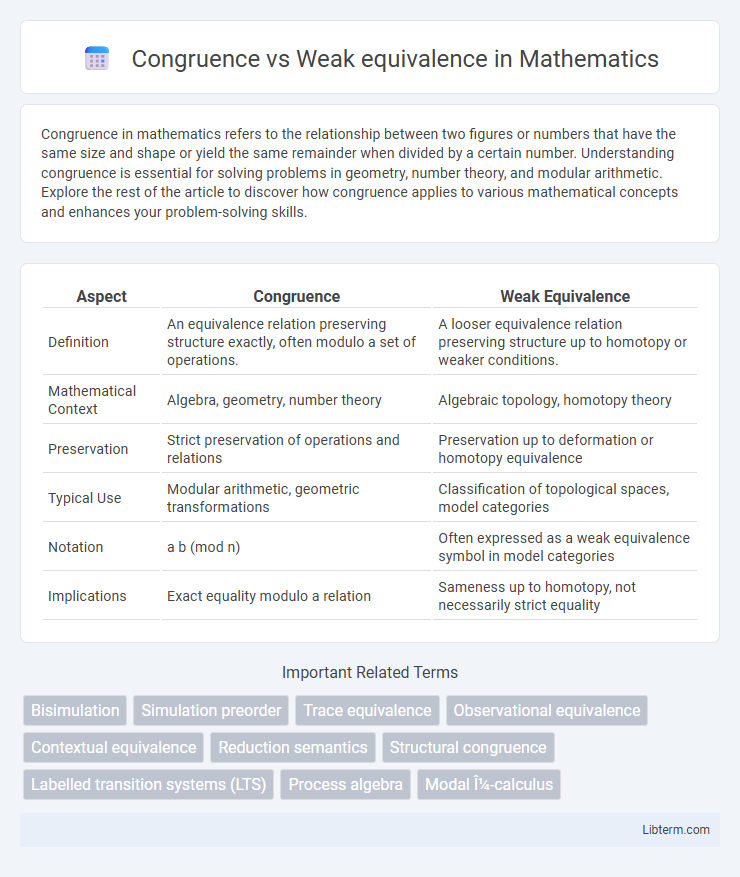
| Aspect | Congruence | Weak Equivalence |
|---|---|---|
| Definition | An equivalence relation preserving structure exactly, often modulo a set of operations. | A looser equivalence relation preserving structure up to homotopy or weaker conditions. |
| Mathematical Context | Algebra, geometry, number theory | Algebraic topology, homotopy theory |
| Preservation | Strict preservation of operations and relations | Preservation up to deformation or homotopy equivalence |
| Typical Use | Modular arithmetic, geometric transformations | Classification of topological spaces, model categories |
| Notation | a b (mod n) | Often expressed as a weak equivalence symbol in model categories |
| Implications | Exact equality modulo a relation | Sameness up to homotopy, not necessarily strict equality |
Introduction to Process Equivalence
Process equivalence in concurrency theory compares the behavior of different systems to determine when they exhibit identical or sufficiently similar actions. Congruence is a strong form of equivalence that ensures equivalent processes remain indistinguishable under all contexts and compositions, preserving substitution properties. Weak equivalence relaxes this by abstracting away from internal or silent actions (t-transitions), allowing systems to be considered equivalent despite some hidden behavioral differences.
Defining Congruence in Formal Systems
Congruence in formal systems is defined as an equivalence relation that is compatible with the system's operations, meaning if two elements are congruent, replacing one with the other in any context preserves equivalence. Weak equivalence, by contrast, allows for a looser form of equivalence that may not be preserved under all system operations or contextual replacements. The defining characteristic of congruence ensures structural substitution consistency, which is critical for maintaining integrity in formal proofs and algebraic reasoning.
Understanding Weak Equivalence
Weak equivalence generalizes the concept of congruence by allowing structural similarities without strict identity, crucial in homotopy theory and category theory. Understanding weak equivalence involves recognizing morphisms that induce isomorphisms in homotopy groups or derived categories, reflecting equivalence up to deformation rather than strict equality. This subtle distinction enables flexible modeling of mathematical objects where exact congruence is too rigid, facilitating advanced equivalence frameworks in algebraic topology and abstract algebra.
Key Differences Between Congruence and Weak Equivalence
Congruence in mathematics requires two objects to be identical in shape and size, preserving distance and angles exactly, while weak equivalence allows a broader comparison, often preserving some but not all structural properties or relations. Key differences lie in the strictness of conditions: congruence demands exact matching under rigid transformations, whereas weak equivalence permits transformations that may alter some metrics but maintain essential characteristics. This distinction makes congruence suitable for precise geometric analysis, whereas weak equivalence applies in contexts like category theory or homotopy, where flexibility in equivalence is crucial.
Importance in Process Calculi
Congruence ensures that equivalence relations remain preserved under all contexts within process calculi, enabling robust reasoning about process behavior and compositional verification. Weak equivalence abstracts away from internal actions (t-transitions), allowing comparisons that focus on observable behavior rather than internal steps, but it may fail to be a congruence in certain process algebras. Maintaining congruence properties in weak equivalence is crucial for modularity and correctness proofs, making it a central concern in the design and analysis of process calculi like CCS and p-calculus.
Applications in Verification and Model Checking
Congruence ensures equivalence is preserved in all contexts, making it essential for compositional verification where system components are analyzed independently. Weak equivalence, which abstracts internal actions, suits model checking by reducing state space while preserving observable behaviors, facilitating the verification of concurrent systems. Applying congruence enables modular reasoning in protocol verification, whereas weak equivalence optimizes automated verification tools by simplifying system models without losing critical behavioral properties.
Examples Illustrating Congruence
Congruence in mathematics refers to the relation where two numbers or figures have the same remainder when divided by a specified modulus, exemplified by 17 5 (mod 12) since both leave a remainder of 5 when divided by 12. In contrast, weak equivalence involves a broader notion of similarity that does not require strict modular equality, often used in algebraic or logical contexts where structures behave similarly under certain conditions but are not identical. For instance, in group theory, two groups may be weakly equivalent if there exists a homomorphism preserving some structure, whereas congruent numbers have exact modular equality.
Examples Demonstrating Weak Equivalence
Weak equivalence in mathematical contexts often refers to relationships where two structures share essential properties without being strictly identical, such as homotopy equivalences in topology where spaces can be continuously deformed into each other but are not necessarily congruent. For example, two topological spaces that are homotopy equivalent have the same fundamental group and homology groups, representing weak equivalence, even though they may differ in geometric shape or size. Contrarily, congruence implies an isometric or exact equivalence, maintaining all distances and angles, exemplified by two congruent triangles having identical side lengths and angles.
Challenges in Distinguishing Equivalences
Distinguishing congruence from weak equivalence poses significant challenges due to their nuanced definitions in algebraic structures and model theory. Congruence requires a stricter form of equivalence compatible with operations, often represented by kernel pairs of homomorphisms, whereas weak equivalence, such as homotopy or quasi-isomorphism, involves more flexible criteria preserving structures up to certain transformations. Identifying these differences demands advanced categorical and homotopical analysis, often complicated by the presence of non-trivial morphisms and the context-dependent nature of equivalence relations.
Conclusion: Choosing the Right Equivalence Approach
Choosing the right equivalence approach depends on the context and precision required, as congruence ensures strict equivalence under all operations, making it ideal for formal proofs and algebraic structures. Weak equivalence offers flexibility by allowing equivalence under broader, less strict conditions, suitable for applications where approximate or functional similarity suffices. Evaluating the trade-offs between strictness and practicality ensures the selection of the most effective equivalence method for specific semantic or computational tasks.
Congruence Infographic
 libterm.com
libterm.com