An accumulation point of a set refers to a value where every neighborhood around it contains infinitely many points from that set. Understanding accumulation points is essential for analyzing limits, continuity, and convergence in mathematical analysis. Explore the rest of the article to deepen your understanding of how accumulation points influence various mathematical concepts.
Table of Comparison
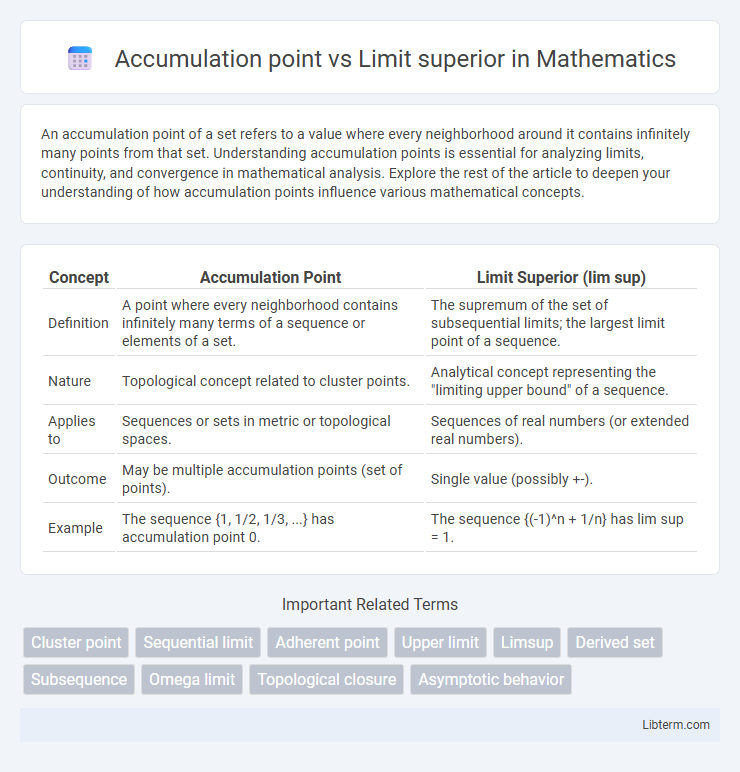
| Concept | Accumulation Point | Limit Superior (lim sup) |
|---|---|---|
| Definition | A point where every neighborhood contains infinitely many terms of a sequence or elements of a set. | The supremum of the set of subsequential limits; the largest limit point of a sequence. |
| Nature | Topological concept related to cluster points. | Analytical concept representing the "limiting upper bound" of a sequence. |
| Applies to | Sequences or sets in metric or topological spaces. | Sequences of real numbers (or extended real numbers). |
| Outcome | May be multiple accumulation points (set of points). | Single value (possibly +-). |
| Example | The sequence {1, 1/2, 1/3, ...} has accumulation point 0. | The sequence {(-1)^n + 1/n} has lim sup = 1. |
Introduction to Accumulation Points and Limit Superior
An accumulation point of a sequence is a value that the sequence elements approach infinitely often, capturing the cluster behavior within the sequence. Limit superior, or lim sup, represents the supremum of the set of subsequential limits, providing the greatest accumulation point of the sequence. Understanding accumulation points is essential for grasping the concept of limit superior, which formalizes the idea of the largest value approached by subsequences.
Defining Accumulation Points
An accumulation point of a sequence is a value where infinitely many elements of the sequence cluster arbitrarily close. The limit superior of a sequence is the greatest accumulation point among all its subsequences. Identifying accumulation points involves analyzing subsequential limits, highlighting values that subsequences approach infinitely often.
Understanding Limit Superior
Limit superior (lim sup) of a sequence is the supremum of its set of accumulation points, representing the largest subsequential limit. It captures the eventual upper bound behavior of the sequence, even when the sequence does not converge. Understanding limit superior is crucial for analyzing oscillatory or non-convergent sequences, as it provides insight into their long-term oscillation and boundary behavior.
Key Differences Between Accumulation Point and Limit Superior
An accumulation point of a sequence is a value that subsequences of the sequence approach infinitely often, while the limit superior (lim sup) is the supremum of the set of all accumulation points, representing the greatest cluster value. Accumulation points can be multiple and scattered, but the limit superior provides a single upper bound to these points, emphasizing the maximal limiting behavior of the sequence. Understanding this distinction clarifies that accumulation points describe local convergence properties, whereas the limit superior captures the global upper trend of the sequence's values.
Mathematical Formal Definitions
An accumulation point (or limit point) of a sequence \((x_n)\) is a value \(L\) such that every neighborhood of \(L\) contains infinitely many terms of the sequence, formally, for every \(\epsilon > 0\), there exist infinitely many \(n \in \mathbb{N}\) with \(|x_n - L| < \epsilon\). The limit superior (lim sup) of a sequence \((x_n)\) is defined as the supremum of the set of its accumulation points, or equivalently, \(\limsup_{n \to \infty} x_n = \lim_{n \to \infty} \sup_{k \geq n} x_k\). While every limit superior is an accumulation point or the supremum of accumulation points, not all accumulation points correspond to the limit superior, which captures the "largest" limit behavior of the sequence.
Common Examples in Sequences and Sets
An accumulation point of a sequence is a value to which subsequences converge infinitely often, such as 0 in the sequence 1/n and 1; the limit superior (lim sup) represents the supremum of these accumulation points, capturing the largest cluster value or "ultimate upper bound." For example, for the sequence defined by x_n = (-1)^n + 1/n, the accumulation points are 1 and -1, with the lim sup equal to 1 and the lim inf equal to -1. In sets like {1/n : n N}, 0 is an accumulation point but not a member of the set, illustrating how accumulation points extend beyond the actual elements to describe limit behavior.
Significance in Real Analysis
The accumulation point of a sequence identifies values where subsequences converge, crucial for understanding the sequence's local behavior in real analysis. Limit superior (lim sup) captures the supremum of subsequential limits, revealing the sequence's ultimate upper boundary and oscillation tendencies. Both concepts play key roles in analyzing convergence properties, stability, and the structure of sets defined by sequences.
Visual Interpretation and Graphical Representation
Accumulation points represent values where a sequence has infinitely many terms arbitrarily close, often visualized as cluster points on a graph where sequence plot points densely gather. Limit superior, or lim sup, is the supremum of the set of accumulation points, depicted graphically as the horizontal line beyond which sequence values rarely exceed after some index. Visual interpretation shows accumulation points as scatter regions on the timeline of sequence values, while limit superior appears as the highest horizontal boundary capturing the upper envelope of these cluster regions.
Common Pitfalls and Misconceptions
Accumulation points are often confused with limit superior because both describe limiting behaviors of sequences, but accumulation points refer to the values that subsequences converge to, whereas limit superior is the supremum of all accumulation points. A common misconception is assuming limit superior always exists as a limit of the sequence itself, ignoring that it can be a boundary value that is never actually attained by the sequence. Misinterpreting accumulation points as unique limit points causes errors in analysis, especially in non-monotone or oscillatory sequences where multiple accumulation points can exist simultaneously.
Applications and Further Implications in Mathematics
Accumulation points identify values where sequences cluster infinitely often, crucial for studying convergence behavior and topological properties in real analysis and metric spaces. Limit superior (lim sup) captures the supremum of subsequential limits, providing a powerful tool for bounding oscillatory sequences and analyzing convergence in probability theory and ergodic processes. Applications of accumulation points and limit superior extend to functional analysis, optimization, and dynamical systems, enabling refined understanding of stability, recurrence, and asymptotic behavior.
Accumulation point Infographic
 libterm.com
libterm.com