Hodge modules provide a powerful framework in algebraic geometry, combining Hodge theory and D-module theory to study the complex structure of algebraic varieties. These modules enable deeper understanding of the interaction between topology, geometry, and analysis, enhancing tools for researchers in the field. Explore the following article to discover how Hodge modules can advance your mathematical insights.
Table of Comparison
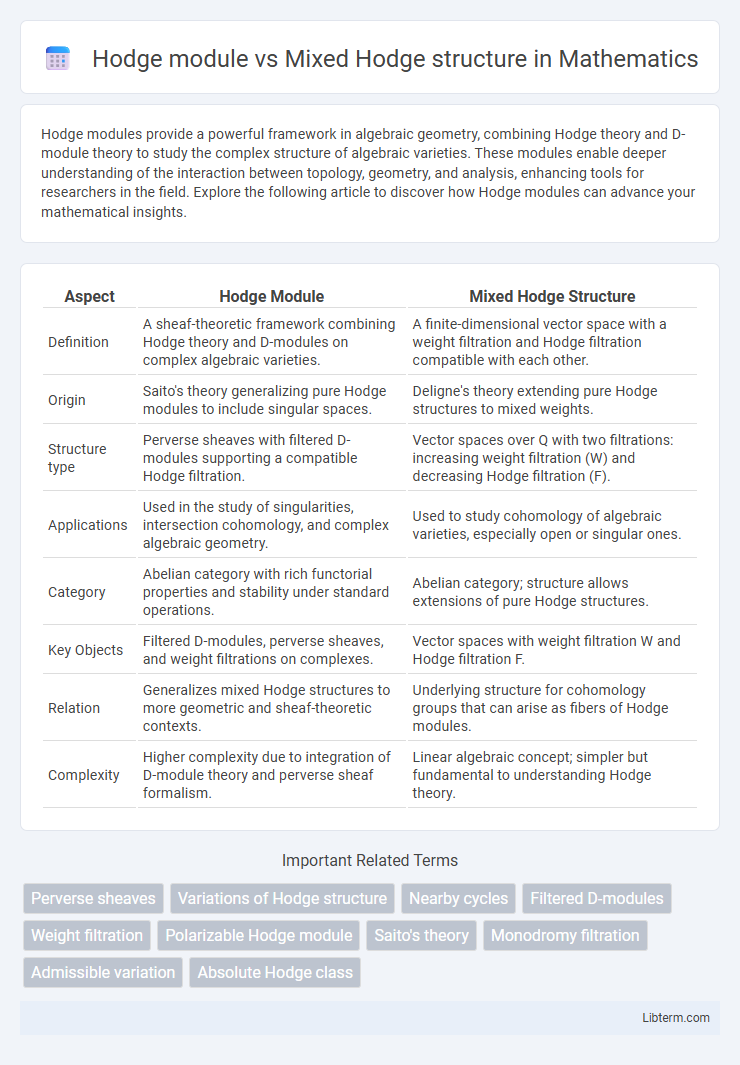
| Aspect | Hodge Module | Mixed Hodge Structure |
|---|---|---|
| Definition | A sheaf-theoretic framework combining Hodge theory and D-modules on complex algebraic varieties. | A finite-dimensional vector space with a weight filtration and Hodge filtration compatible with each other. |
| Origin | Saito's theory generalizing pure Hodge modules to include singular spaces. | Deligne's theory extending pure Hodge structures to mixed weights. |
| Structure type | Perverse sheaves with filtered D-modules supporting a compatible Hodge filtration. | Vector spaces over Q with two filtrations: increasing weight filtration (W) and decreasing Hodge filtration (F). |
| Applications | Used in the study of singularities, intersection cohomology, and complex algebraic geometry. | Used to study cohomology of algebraic varieties, especially open or singular ones. |
| Category | Abelian category with rich functorial properties and stability under standard operations. | Abelian category; structure allows extensions of pure Hodge structures. |
| Key Objects | Filtered D-modules, perverse sheaves, and weight filtrations on complexes. | Vector spaces with weight filtration W and Hodge filtration F. |
| Relation | Generalizes mixed Hodge structures to more geometric and sheaf-theoretic contexts. | Underlying structure for cohomology groups that can arise as fibers of Hodge modules. |
| Complexity | Higher complexity due to integration of D-module theory and perverse sheaf formalism. | Linear algebraic concept; simpler but fundamental to understanding Hodge theory. |
Introduction to Hodge Modules and Mixed Hodge Structures
Hodge modules generalize classical Hodge theory by incorporating perverse sheaves and D-modules, enabling the study of singular varieties and deepening the understanding of variation of Hodge structures. Mixed Hodge structures extend pure Hodge structures by allowing a weight filtration along with the Hodge filtration, providing a framework to analyze the cohomology of complex algebraic varieties with singularities or non-compactness. These frameworks interconnect complex algebraic geometry, representation theory, and topology by encoding refined geometric and topological information through filtered and graded structures.
Historical Development and Motivation
Hodge modules, introduced by Morihiko Saito in the 1980s, generalize classical mixed Hodge structures by incorporating sheaf-theoretic and D-module techniques to handle singularities and constructible complexes. Mixed Hodge structures, developed earlier by Pierre Deligne, arose from the need to extend Hodge theory beyond smooth projective varieties to singular and non-compact algebraic varieties, capturing the interplay between topology and algebraic geometry. The historical development of Hodge modules reflects the transition from purely algebraic and topological invariants to more refined tools involving Hodge filtrations compatible with perverse sheaves and the derived category framework.
Foundational Definitions
A Hodge module is a sophisticated sheaf-theoretic object combining perverse sheaves with Hodge filtration, providing a framework for studying singular varieties through Saito's theory. Mixed Hodge structures, introduced by Deligne, generalize classical pure Hodge structures by incorporating weight filtrations to handle cohomology of singular or non-compact varieties. While mixed Hodge structures describe graded vector spaces with compatible filtrations, Hodge modules extend these concepts to derived categories and D-modules, enabling the analysis of complex geometric and topological phenomena.
Key Properties and Features
Hodge modules extend the concept of mixed Hodge structures by incorporating sheaf-theoretic and D-module techniques, enabling the study of singular spaces and their cohomology with additional functorial properties. Mixed Hodge structures provide a finite-dimensional rational vector space equipped with two filtrations--weight and Hodge filtrations--that satisfy specific compatibility rules crucial for analyzing the topology of complex algebraic varieties. The key feature of Hodge modules lies in their ability to bridge geometric aspects with algebraic and analytic tools, offering a more flexible and powerful framework for capturing variations in Hodge theory beyond smooth projective settings.
Construction Methods
Hodge modules are constructed using the framework of D-modules and perverse sheaves, incorporating filtration by weight and Hodge filtration which generalizes variations of Hodge structures on singular spaces. Mixed Hodge structures are built by applying Deligne's canonical filtration techniques on cohomology groups, organizing them into a weight filtration and a Hodge filtration to control their mixed nature. The construction of Hodge modules involves derived category methods and the theory of nearby and vanishing cycles, while mixed Hodge structures rely primarily on algebraic and topological methods focused on cohomological gradings.
Main Differences between Hodge Modules and Mixed Hodge Structures
Hodge modules extend mixed Hodge structures by incorporating the action of differential operators and perverse sheaves, enabling them to handle singularities and complex algebraic varieties more effectively. Mixed Hodge structures consist solely of filtrations on cohomology groups, providing graded pieces that reflect geometric and topological properties without additional sheaf-theoretic data. The main difference lies in Hodge modules' ability to unify Hodge theory with D-module theory, offering a powerful framework for studying variations and degenerations beyond the scope of classical mixed Hodge structures.
Examples and Illustrative Cases
Hodge modules extend the concept of mixed Hodge structures by incorporating D-module and perverse sheaf frameworks, enabling advanced analysis of singularities and variations in complex algebraic geometry. For instance, the intersection cohomology of singular algebraic varieties carries a pure Hodge module, while mixed Hodge structures appear in the cohomology of open or non-compact varieties, encoding weight filtrations reflecting geometric degeneration. Illustrative cases include the study of vanishing cycles around isolated singularities, where Hodge modules capture refined invariants beyond what mixed Hodge structures provide alone.
Applications in Algebraic Geometry and Representation Theory
Hodge modules provide a powerful framework for studying singularities and perverse sheaves in algebraic geometry, enabling the extension of classical Hodge theory to complex algebraic varieties with singularities. Mixed Hodge structures, by contrast, offer a refined tool to analyze the cohomology of algebraic varieties with a filtration that captures the interaction between topology and algebraic geometry, crucial for understanding variations of Hodge structure. In representation theory, Hodge modules facilitate the geometric construction of representations of algebraic groups via the decomposition theorem, while mixed Hodge structures illuminate the structure of weight filtrations on cohomology groups, deepening insights into motives and arithmetic aspects of algebraic varieties.
Current Research Trends
Current research on Hodge modules emphasizes their role in extending variations of Hodge structures to singular spaces, integrating D-module theory and perverse sheaves for advanced applications in algebraic geometry. Mixed Hodge structures continue to be investigated for their intricate weight filtrations and their influence on the study of degenerations and limit mixed Hodge structures in families of varieties. Recent developments focus on synthesizing these frameworks to better understand the interaction between singularities, cohomology, and representation theory within the broader context of Hodge theory.
Conclusion and Future Directions
Hodge modules extend the framework of mixed Hodge structures by incorporating deeper geometric and categorical properties, enabling more refined invariants in complex algebraic geometry. The development of Hodge module theory opens new pathways for studying singularities, representation theory, and arithmetic geometry through enhanced filtration and functorial techniques. Future research will likely explore stronger computational tools, broader applications in non-abelian Hodge theory, and potential generalizations to motivic contexts.
Hodge module Infographic
 libterm.com
libterm.com