Injective is a decentralized exchange protocol that offers fast, secure, and trustless trading of derivatives and spot assets with zero gas fees. By integrating layer-2 scaling solutions and cross-chain compatibility, it empowers users to trade seamlessly across multiple blockchains while maintaining full custody of their funds. Discover how Injective can transform your trading experience in the rest of this article.
Table of Comparison
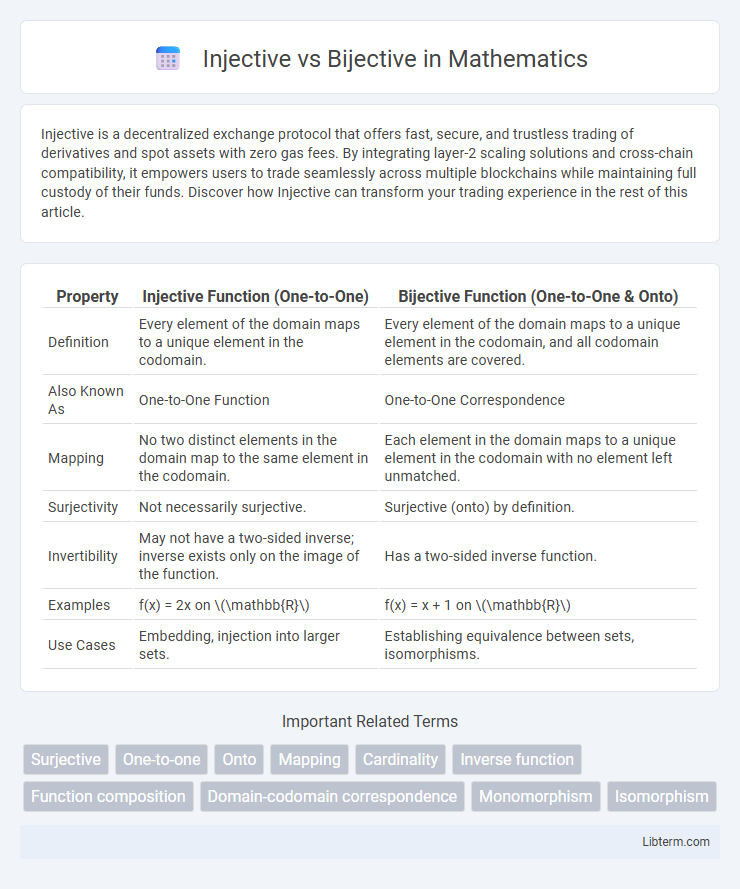
| Property | Injective Function (One-to-One) | Bijective Function (One-to-One & Onto) |
|---|---|---|
| Definition | Every element of the domain maps to a unique element in the codomain. | Every element of the domain maps to a unique element in the codomain, and all codomain elements are covered. |
| Also Known As | One-to-One Function | One-to-One Correspondence |
| Mapping | No two distinct elements in the domain map to the same element in the codomain. | Each element in the domain maps to a unique element in the codomain with no element left unmatched. |
| Surjectivity | Not necessarily surjective. | Surjective (onto) by definition. |
| Invertibility | May not have a two-sided inverse; inverse exists only on the image of the function. | Has a two-sided inverse function. |
| Examples | f(x) = 2x on \(\mathbb{R}\) | f(x) = x + 1 on \(\mathbb{R}\) |
| Use Cases | Embedding, injection into larger sets. | Establishing equivalence between sets, isomorphisms. |
Introduction to Functions: Injective vs Bijective
Injective functions map each element of the domain to a unique element in the codomain, ensuring no two distinct inputs share the same output. Bijective functions establish a one-to-one correspondence between domain and codomain, guaranteeing both injectivity and surjectivity, meaning every element in the codomain is uniquely paired with an element in the domain. Understanding injective versus bijective functions is fundamental in grasping function behavior, invertibility, and mapping structures in mathematics.
Definitions: What Are Injective and Bijective Functions?
Injective functions, also known as one-to-one functions, ensure that each element in the domain maps to a unique element in the codomain, preventing any two distinct inputs from sharing the same output. Bijective functions combine injectivity and surjectivity, meaning every element in the domain maps to a unique element in the codomain, and every element in the codomain is mapped by exactly one element in the domain, establishing a perfect pairing. Understanding these definitions is fundamental in fields like mathematics and computer science for analyzing function behavior and inverse functions.
Mathematical Notation and Formal Descriptions
Injective functions, denoted as \( f: A \to B \), satisfy the condition \( f(a_1) = f(a_2) \implies a_1 = a_2 \), ensuring that distinct elements in domain \( A \) map to distinct elements in codomain \( B \). Bijective functions establish a one-to-one correspondence between sets \( A \) and \( B \), defined by \( f: A \to B \) being both injective and surjective, and therefore possess an inverse function \( f^{-1}: B \to A \) such that \( f^{-1}(f(a)) = a \) for all \( a \in A \). Formally, a bijection satisfies the conditions \( \exists f^{-1} \) where \( f \circ f^{-1} = \text{id}_B \) and \( f^{-1} \circ f = \text{id}_A \), indicating perfect invertibility between the sets.
Key Properties of Injective (One-to-One) Functions
Injective functions, also known as one-to-one functions, map each element of the domain to a unique element in the codomain, ensuring no two distinct inputs share the same output. This property guarantees that the function can be reversed on its image, making the inverse function well-defined over the range. Unlike bijective functions, injective functions do not require every element of the codomain to be mapped, emphasizing their key role in establishing uniqueness without surjectivity.
Key Properties of Bijective (One-to-One and Onto) Functions
Bijective functions are characterized by being both injective (one-to-one) and surjective (onto), ensuring every element in the codomain is mapped by exactly one element in the domain. This unique pairing guarantees an inverse function exists, making bijections crucial in establishing one-to-one correspondences between sets. Key properties of bijective functions include a perfect match between domain and codomain, preserving distinctness and completeness across mappings.
Visual Illustrations: Understanding Through Graphs
Injective functions map each element of the domain to a unique element in the codomain, illustrated on graphs by distinct input points connecting to different output points without overlap. Bijective functions combine injectivity and surjectivity, shown visually as a perfect one-to-one correspondence between domain and codomain points, covering all outputs with no repetitions or omissions. Graphs of bijections typically appear as a curve or line where every element in the codomain is paired with exactly one unique element in the domain, making the relationship invertible.
Real-World Applications of Injective Functions
Injective functions, also known as one-to-one functions, play a crucial role in cryptography by ensuring unique encryption keys map to distinct ciphertexts, preventing data collisions. In computer science, injective mappings facilitate memory address allocation where each variable corresponds uniquely to a memory slot, optimizing resource management. These functions are fundamental in bioinformatics for gene sequencing, guaranteeing that each sequence maps distinctly to a species or claim in genetic research.
Real-World Applications of Bijective Functions
Bijective functions play a crucial role in cryptography, enabling secure encryption and decryption by establishing a one-to-one correspondence between plaintext and ciphertext. In computer science, they facilitate efficient data encoding and compression, ensuring lossless data recovery through reversible transformations. Moreover, bijective functions are fundamental in database management for creating unique key-value mappings, enhancing data integrity and retrieval efficiency.
Distinguishing Between Injective, Surjective, and Bijective
Injective functions map each element of the domain to a unique element in the codomain, ensuring no two inputs share the same output, thus preserving distinctness. Surjective functions cover every element in the codomain, meaning every target value has at least one preimage in the domain. Bijective functions combine injective and surjective properties, creating a one-to-one correspondence between domain and codomain, enabling invertibility and perfect pairing of elements.
Summary Table: Injective vs Bijective Functions
Injective functions map distinct elements of the domain to distinct elements of the codomain, ensuring no two domain elements share the same image, while bijective functions are both injective and surjective, establishing a perfect one-to-one correspondence between domain and codomain. In the summary table comparing injective and bijective functions, injective functions feature unique outputs but may not cover the entire codomain, whereas bijective functions guarantee every element in the codomain is mapped to by exactly one domain element. The table highlights injectivity as a requirement for bijectivity and distinguishes surjectivity as the key additional property needed for a function to be bijective.
Injective Infographic
 libterm.com
libterm.com