Hodge filtration is a fundamental concept in algebraic geometry and complex analysis, describing a descending sequence of subspaces in the cohomology of a smooth projective variety. This filtration captures the intricate relationship between differential forms and the topological structure of complex manifolds, playing a crucial role in Hodge theory. Explore the rest of the article to understand how Hodge filtration impacts modern mathematical research and its applications.
Table of Comparison
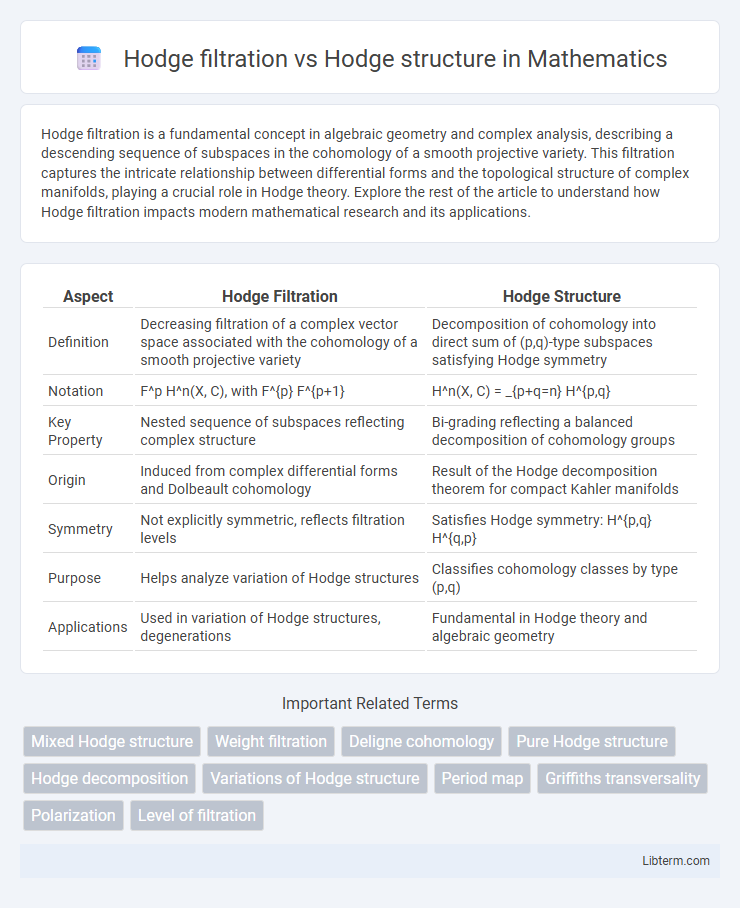
| Aspect | Hodge Filtration | Hodge Structure |
|---|---|---|
| Definition | Decreasing filtration of a complex vector space associated with the cohomology of a smooth projective variety | Decomposition of cohomology into direct sum of (p,q)-type subspaces satisfying Hodge symmetry |
| Notation | F^p H^n(X, C), with F^{p} F^{p+1} | H^n(X, C) = _{p+q=n} H^{p,q} |
| Key Property | Nested sequence of subspaces reflecting complex structure | Bi-grading reflecting a balanced decomposition of cohomology groups |
| Origin | Induced from complex differential forms and Dolbeault cohomology | Result of the Hodge decomposition theorem for compact Kahler manifolds |
| Symmetry | Not explicitly symmetric, reflects filtration levels | Satisfies Hodge symmetry: H^{p,q} H^{q,p} |
| Purpose | Helps analyze variation of Hodge structures | Classifies cohomology classes by type (p,q) |
| Applications | Used in variation of Hodge structures, degenerations | Fundamental in Hodge theory and algebraic geometry |
Introduction to Hodge Theory
Hodge filtration is a decreasing sequence of subspaces in the complexified cohomology group that captures the layered structure of differential forms in Hodge theory. Hodge structure refers to the decomposition of the cohomology of a smooth projective variety into a direct sum of Hodge components, reflecting the interplay between algebraic and analytic properties. Understanding the relationship between Hodge filtration and Hodge structure is fundamental in Hodge theory for studying variations of complex structures and periods of integrals.
Defining Hodge Filtration
Hodge filtration is a decreasing filtration on the complexified cohomology groups of a smooth projective variety, defined by subspaces \( F^p H^n(X, \mathbb{C}) \) that encode the complex structure via holomorphic forms. It plays a fundamental role in decomposing the cohomology into pieces related to the Hodge structure, which combines this filtration with its conjugate to produce the Hodge decomposition. The Hodge filtration directly determines the Hodge structure by specifying the filtration levels that reflect the variation of complex structures in Hodge theory.
Understanding Hodge Structure
The Hodge structure is a fundamental concept in algebraic geometry and complex geometry, defined by decomposing the cohomology of a smooth projective variety into a direct sum of complex subspaces H^{p,q} satisfying Hodge symmetry. The Hodge filtration, a decreasing filtration of the cohomology vector space, encodes the same data as the Hodge decomposition but in a more flexible form suitable for variation in families of varieties. Understanding Hodge structure involves analyzing how these filtrations interact with the integral cohomology, providing deep insights into the geometric and topological properties of algebraic varieties.
Key Differences: Filtration vs Structure
Hodge filtration is a descending sequence of subspaces on the complexified cohomology groups that encode the complex structure, whereas a Hodge structure is the decomposition of these cohomology groups into a direct sum of (p,q)-types satisfying specific symmetry conditions. The filtration provides a more flexible, stepwise view capturing the gradations, while the structure offers a rigid, fully decomposed framework essential for identifying the Hodge numbers. Hodge filtration is primarily used in variations of Hodge structures and degenerations, contrasting with the static, integral lattice presence defining Hodge structures.
Construction of the Hodge Filtration
The Hodge filtration is constructed by defining a decreasing sequence of subbundles on the complexified cohomology groups, encoding variations of Hodge structures through holomorphic data. This filtration arises naturally from the splitting of the complexified cohomology in terms of (p,q)-types, reflecting the geometric decomposition of differential forms on a Kahler manifold. The interplay between the Hodge filtration and the underlying integral Hodge structure determines the rich algebraic and analytic properties central to Hodge theory and its applications.
The Role of Hodge Structure in Algebraic Geometry
Hodge structure provides a fundamental framework in algebraic geometry by decomposing the cohomology of complex algebraic varieties into pieces that reflect geometric and topological properties. The Hodge filtration organizes these decompositions into a decreasing sequence of subspaces, capturing variations in complex structure through filtrations on cohomology groups. This interplay between Hodge structure and filtration enables deep insights into the study of periods, variations of Hodge structures, and the formulation of the Hodge conjecture.
Applications of Hodge Filtration
Hodge filtration is a fundamental tool in complex geometry and algebraic topology, serving as a descending filtration on the de Rham cohomology that helps analyze the subtle structure of complex algebraic varieties. It plays a critical role in mirror symmetry, deformation theory, and period mappings by organizing cohomology groups into graded pieces connected to Hodge structures. Applications of Hodge filtration extend to mixed Hodge theory in singular varieties and the study of variations of Hodge structures in families of algebraic varieties, facilitating deep insights into their geometric and arithmetic properties.
Interdependence of Filtration and Structure
Hodge filtration and Hodge structure are deeply interdependent, where the Hodge filtration provides a descending sequence of subspaces that reconstruct the Hodge decomposition defining the Hodge structure on a cohomology group. The filtration's properties determine the pure types of the Hodge structure, encoding complex geometric information through graded pieces associated with holomorphic forms. This interplay allows the extraction of refined invariants in algebraic geometry, linking differential forms and topological cohomology classes in a coherent framework.
Examples: Comparing Hodge Filtration and Structure
Hodge filtration on the de Rham cohomology of a smooth projective variety organizes cohomology groups into a descending sequence of subspaces, such as the filtration \( F^pH^n = \bigoplus_{r \geq p} H^{r,n-r} \) on \( H^n \). In contrast, a Hodge structure provides a bigrading \( H^n = \bigoplus_{p+q=n} H^{p,q} \) with the decomposition respecting complex conjugation, exemplified by the Hodge decomposition of a Kahler manifold's cohomology. For example, the elliptic curve has a Hodge structure with \( H^{1,0} \) and \( H^{0,1} \) components, while its Hodge filtration collapses these into a single filtration step \( F^1 \subset H^1 \).
Summary and Future Perspectives
Hodge filtration is a decreasing sequence of subspaces within a complex vector space that encodes the complex structure of a variety's cohomology, while a Hodge structure is a more refined decomposition into direct sums capturing both the filtration and its conjugate symmetry. The distinction is crucial for understanding variations of Hodge structures and period mappings, which have profound implications in algebraic geometry and arithmetic geometry. Future research aims to deepen the relationship between Hodge filtrations, mixed Hodge structures, and their applications in non-abelian Hodge theory and mirror symmetry.
Hodge filtration Infographic
 libterm.com
libterm.com